ফটোইলেকট্রিক ইফেক্টের ক্রিয়াকৌশল জানবার দরুণ এ সম্পর্কে আমরা নিশ্চিত হতে পেরেছিলাম যে – তরঙ্গ কণাধর্মী আচরণ করতে পারে। এ ব্যাপারে জ্ঞাত হবার পর বিজ্ঞানীরা এটার বিপরীত সম্ভাব্যতা নিয়েও ভাবতে থাকেন – বস্তুরও কি তাহলে তরঙ্গ আকারে থাকতে পারে না? মজার ঘটনা ঘটল তখন যখন ১৯২৪ সালে জগৎকে বিস্ময়ে ডুবিয়ে ফরাসী পদার্থবিদ ডি ব্রগলি (De Broglie) সত্যিই ঘোষণা করে বসলেন, হ্যাঁ! বস্তু হিসেবে আমরা যা দেখি তাদেরও আছে তরঙ্গধর্ম।
সমীকরণের আলাপ অনেক করা যাবে, তার পূর্বে এই অদ্ভুত কিসিমের কথার একটা বিহিত করা উচিত। বস্তু আবার তরঙ্গ হয় কীভাবে রে বাবা? বস্তু বলতে আমরা তো বুঝি এই যে আমার হাতের কাছের মাউস বা ফোনটা, দেয়ালে থাকা ঐ ঘড়িটা কিংবা আমার খেলার ক্রিকেট কিংবা ফুটবলটা, এদের সাথে তরঙ্গ ব্যাপারটা আদৌ কি যায়? তরঙ্গ মানে হল পুকুরের পানির স্পন্দনে দেখা ঢেউ, আমার কানে শব্দ আসার পন্থা। আঁকাবাঁকা চলনের একটা কিছুর সাথে তাহলে আমাদের সামনে থাকা নিরীহ কোনো বস্তু মেলানোর মানে কী?!
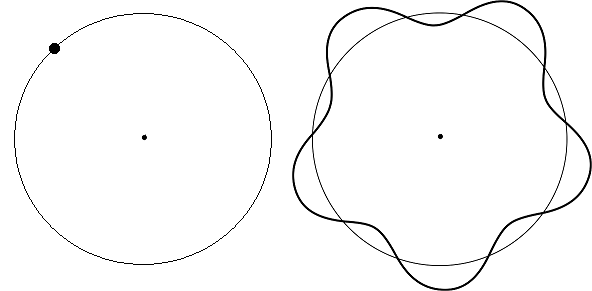
তো সবার আগে এটা বুঝলে একটু সুবিধার হয় যে, এই বস্তু-তরঙ্গের (Matter wave) আলোচনা কোয়ান্টাম ফিজিক্সের আলোচ্য বিষয়। কোয়ান্টাম তত্ত্ব তো আর ইয়া বড় একটা বাস্কেটবলের কথা ভাবতে ভাবতে আসে নি; এসেছে ফোটন, ইলেকট্রন কিংবা পরমাণুর মত ক্ষুদ্রকায় কণাসমূহের আচরণের প্রেক্ষিতে। বস্তু-তরঙ্গ ব্যাপারটা বুঝতে হলে তাই আগেই অত উঁচুতে লাফিয়ে ওঠা যাবে না। এ ব্যাপারে আপাতত আমাদের সবচেয়ে ভাল সাহায্য করতে পারবে একটা ইলেকট্রন। নিচের ছবিটাই দেখ :
ছবিটায় পরমাণুর কক্ষপথে ইলেকট্রনের দুই ধরণের চলা দেখানো হয়েছে। প্রথম উপায়ে ইলেকট্রন শেলের পরিধিকে তার পথ মনে করে বৃত্তাকারে ঘুরছে, দ্বিতীয় ধরণটিতে ইলেকট্রন বৃত্তের উপরই একটা তরঙ্গাকার পথে ঘুরছে। তোমার কাছে কোন ধরণের আবর্তনটা স্বাভাবিক মনে হয়? অবশ্যই প্রথমটা! কারণ আমরা যেসকল বস্তু সচারচর দেখি তারা তো এভাবেই কোনো বৃত্তকে আবর্তন করে। উদাহরণ : একটা চত্বরের চারপাশে কোনো বাসের ঘুরে আসা। ঐ বাস কি ওরকম তরঙ্গাকৃতির ব্রেক ড্যান্স দেয় বল? দেয় না। কিন্তু আমাদের ইলেকট্রন আর একটা বাস তো এক জিনিস নয়। বাসের ভর অতিকায়, তার বেগও ইলেকট্রনের বেগের তুলনায় নগণ্য; অথচ ইলেট্রন ক্ষুদ্র ভরের ও অনেক বেগের একটা কণা। এজন্য এর চলার পথ অবশ্যই আমাদের সনাতনী চিন্তাধারা অনুযায়ী তৈরি হবে না। ইলেকট্রন নিয়ে কথা বলতে গেলে আমাদের প্রবেশ করতে হবে কোয়ান্টাম রাজ্যে যেখানে আমাদের চারপাশে বিরাজমান ট্রেডিশনাল পদার্থবিদ্যার সাথে মিল যৎসামান্য। কোয়ান্টাম পার্টিকেল হিসেবে ইলেকট্রন তাই তার কক্ষপথে চলতে পারবে এমন তরঙ্গ সৃষ্টি করে। মনে হবে – বস্তু যেন হয়ে উঠেছে ঠিক তরঙ্গ!
তাহলে, বড় বস্তুগুলো? তাদের ক্ষেত্রে এমন কিছু হতে দেখি না কেন? এ প্রশ্নের উত্তর পাব আরেকটু পরে।
খানিকটা কথা হোক ব্রগলির বস্তু-তরঙ্গ ভিত্তিক তাত্ত্বিক আলোচনায়। ব্রগলির সমীকরণ আসলে দু’টি বিখ্যাত ও মৌলিক সূত্র থেকে বারকয়েক প্রতিস্থাপনের মাধ্যমে পাওয়া একটা নতুন সম্পর্ক। আমরা সেই মেইনস্ট্রিম প্রতিপাদনে যাব না, কেবল ব্রগলির চিন্তাধারা ও পরিকল্পনা সাদাসিধেভাবে বোঝার চেষ্টা করব। খুব সহজ করে উপস্থাপন করলে – আমরা জানি, কোয়ান্টাম তত্ত্বে আলোর কোয়ান্টা বা ফোটনের নিশ্চল ভর শূন্য বলে স্বীকার করে নেওয়া হয়; তথাপি এর নির্দিষ্ট ও অশূন্য ভরবেগ (p) আছে বলে ধরে নেওয়া হয়। এখন এই ভরবেগ p=h/λ লেখা যায় যেখানে h হল প্ল্যাঙ্কের ধ্রুবক (6.62606957 × 10-34 m2kg/s) এবং λ হল ঐ ফোটন যে আলো থেকে পাওয়া যায় তার তরঙ্গদৈর্ঘ্য। ফোটনের এই ভরবেগ হিসাব করতে গিয়ে দেখ, আলোর কণাধর্ম (ভরবেগ, p) আর তরঙ্গধর্ম (তরঙ্গদৈর্ঘ্য, λ) একাকার হয়ে গেছে যা ফটোইলেক্ট্রিক ইফেক্টের কল্যাণে আর অবাক করা কোনো ব্যাপার নয়। কিন্তু এখন আসবে আমরা যাদের প্রকৃত বস্তু বলে দেখি তাদের কথা। তাদের ভরবেগ বলতে আমরা ভর m ও বেগ v এর গুণফল mv কে বুঝি যেরকম প্রকাশ ফোটনের ক্ষেত্রে করা সম্ভব নয় কারণ ফোটনের নিশ্চল ভর বলতে কিছুই নেই অথচ বিশাল সাইজের বেগ আছে (কেমন অলীক না ব্যাপারটা?)। পক্ষান্তরে অনেক বেশি ভরের ও আলোর সাপেক্ষে তুলনামূলক অনেক কম ভরের বস্তুর জন্য ভরবেগ mv কিন্তু নিশ্চিন্তে লিখে ফেলা যায়। যেহেতু ব্রগলি সাহসী ছিলেন, তিনি বললেন – শুধু p ভরবেগের ফোটন নয়, আমি mv ভরবেগের বস্তুর জন্যও একটা তরঙ্গ কল্পনা করতে চাই যার তরঙ্গদৈর্ঘ্য হবে λ (এটা আলোর তরঙ্গদৈর্ঘ্য এর সমান হতে হবে না, নতুন সিম্বল আনার ঝামেলায় না গিয়ে আমরা এই λ কে এখন থেকে ঐ বস্তুর বলেই জানব)। তাহলে এই বস্তুর জন্যেও তো ভরবেগ mv=h/λ লিখতে পারা উচিত! ব্যস! এটাই তো আমাদের উদ্দিষ্ট ব্রগলির বস্তু-তরঙ্গ সমীকরণ!
কিন্তু তখনকার লোকেরা কি এত সহজেই সব মেনে নেবে? বস্তুর সাথে তরঙ্গ মিলিয়ে একটা কথা বলে দিলেই তো আর হবে না। লাগবে পরীক্ষা নিরীক্ষাপূর্বক এর সত্যতাও। সেই উদ্যোগ তখন নিলেন ডেভিসন ও জার্মার (Davisson and Germer) নামের দু’জন বিজ্ঞানী। তারা ১৯২৭ সালে ইলেকট্রন গান নামের একটা ইলেকট্রন ছোঁড়ার যন্ত্র নিলেন ও তার সামনে রাখলেন নিকেল ধাতুর কেলাস। ইলেকট্রন গান থেকে ইলেকট্রনের বিম (electron beam) ছুঁড়ে মারা হল ঐ কেলাসের উপর এবং তার কারণে চারদিকে ছড়িয়ে ছিটিয়ে পড়তে লাগল ইলেকট্রনগুলো। 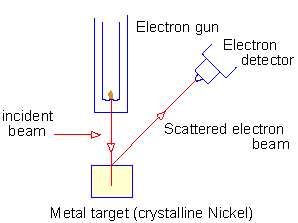
ডেভিসন ও জার্মার ঐ কেলাসের চারপাশে ঘুরতে সক্ষম একটা ডিটেক্টর নিলেন যা মেপে দিতে পারে কোথায়, কোন অবস্থানে ইলেকট্রন সবচেয়ে বেশি ছিটকে আসছে। দেখা গেল, গান থেকে ইলেকট্রন বিমের আসার যে সরলরৈখিক পথ ছিল তার সাথে 50 ডিগ্রি কোণে সর্বোচ্চ তীব্রতা পাওয়া যাচ্ছে ইলেকট্রন ছিটকে আসার, অন্যান্য কৌণিক অবস্থানে যা হচ্ছে না। দুর্দান্ত ব্যাপার হল – ইলেকট্রন না নিয়ে যদি এই পরীক্ষাটা এক্স-রে দিয়ে করা হয় তবেও একইরকম ঘটনা ঘটে; যা ব্র্যাগ (Bragg) নামের একজন বিজ্ঞানী বহু আগেই দেখিয়েছিলেন এবং তার মাধ্যমে এক্স রে এর তরঙ্গদৈর্ঘ্য বের করার একটা সমীকরণও প্রতিপাদন করেছিলেন। মুচকি হেসে ডেভিসনরা ভাবলেন, ইলেকট্রনও যখন একই রকম বৈশিষ্ট্য দেখাচ্ছে তখন একে তরঙ্গ বলতে আর দোষ কী? তারা সরল বিশ্বাসে ব্র্যাগের প্রতিপাদিত সমীকরণ থেকে ইলেকট্রনের তরঙ্গদৈর্ঘ্য বের করলেন 1.65Å। আশ্চর্যজনকভাবে, ইলেকট্রনের ভর, বেগ বসিয়ে ডি ব্রগলির সমীকরণ থেকেও একই ধরণের মান পাওয়া গেল 1.67Å!!!!
মাত্র তিন বছরের একটা তত্ত্বের জন্য এটা যে বিশাল এক অগ্রগতি তা আর বলার অপেক্ষা রাখে কি? আনন্দে ডগমগ হয়ে তাদের স্বীকৃতি দিল সারা বিশ্ব, নোবেল পুরস্কারে ভূষিত হলেন ব্রগলি এবং ডেভিসন-জার্মার। ডি ব্রগলির সমীকরণ সঠিক প্রমাণিত হবার পর নগণ্য হলেও বের করা হল ফোটনের ভর!
এবার আসল চ্যালেঞ্জের পালা। ধর তোমাকে 1g আর 10m/s বেগের একটা বস্তুর তরঙ্গদৈর্ঘ্য হিসাব করতে দিল। তুমি কী করবে? ব্রগলির সমীকরণ ব্যবহার করবে, উত্তরও বলে দেবে একটা, 6.6 × 10-32 m। এখন আমি তোমাকে যদি জিজ্ঞেস করি, “এই যে রেজাল্টটা পেলে, এর প্র্যাক্টিকাল তাৎপর্য কী?” – এবার কিন্তু তুমি কিছুই বলতে পারবে না! কারণ হল – প্রথমত সত্যিই এই মানের কোনো তাৎপর্য নেই!! বড় বস্তুগুলো নিজেরাই অসংখ্য কোয়ান্টাম পার্টিকেলের সমন্বয়ে তৈরি যে পার্টিকেলগুলোর প্রত্যেকের আবার তরঙ্গধর্ম আছে। সুতরাং আস্ত বস্তুটাকে নিয়ে টানাটানি করে আমরা সন্তোষজনক উত্তর পাব না মোটেই। দ্বিতীয়ত, এত্ত ক্ষুদ্র তরঙ্গদৈর্ঘ্য মাপার ব্যবস্থা আমাদের অত্যাধুনিক যন্ত্রপাতি দিয়েও করা সম্ভব নয়। সুতরাং যা মাপতেই পারি না তা নিয়ে শুধু শুধু এত মাথা গরম করার কী আছে? ও থাকুক না ওর মত 😛
বস্তু-তরঙ্গ আলোচনার ইতি টানব এমন কিছু দিয়ে যা আগে দেখেও অদেখা ছিল। জানো কি? ডি ব্রগলির এই বস্তু তরঙ্গকে দায়ী করা যায় তেজস্ক্রিয়তার জন্যেও! ভারী নিউক্লিয়াসযুক্ত অস্থিতিশীল পরমাণুগুলোর তেজস্ক্রিয় ক্ষয়ের অন্যতম প্রধান একটা উপায় হল আলফা ক্ষয় (Alpha Decay)। সবাই জানো, আলফা কণা হল হিলিয়াম নিউক্লিয়াস যা মাতৃপরমাণুর নিউক্লিয়াস হতে বের হয়ে আসার নামই হল আলফা ক্ষয়। একটা কণা হিসেবে আলফা কণার মোটেও সেই শক্তি নেই যা দিয়ে সে পরমাণুর নিউক্লিয়াস থেকে সকল বাধা অতিক্রম করে সাবলীলভাবে বাইরে চলে আসতে পারে। অথচ আমরা কিন্তু এই আলফা ক্ষয়কে একটা স্বতঃস্ফূর্ত প্রক্রিয়া হিসেবেই দেখি। এটার ব্যাখ্যা দেওয়া যায় কণাটির তরঙ্গধর্ম দিয়ে। তরঙ্গধর্ম আছে বলেই সাবঅ্যাটমিক পার্টিকেলগুলো অদ্ভুতুড়ে সব জায়গায় বিচরণে সক্ষম যেখানে তার থাকা উচিত নয়! (ঐ যে ইলেকট্রনের মত, যে পরিধির উপর না থেকে ত্রিমাত্রিক স্থানে ইচ্ছামত নেচে নেচে ঘুরে বেড়াচ্ছে নিউক্লিয়াসের চারপাশে)… আলফা কণাও তাহলে অমন তরঙ্গাকারে বিরাজ করে পরমাণুর ব্যুহ ভেদ করে বাইরে চলে আসতে পারে বৈ কি!

λ = h/mc সমীকরণটি এসেছে E=mc^2 থেকে । c এর জায়গায় v বসালে আবার e=mv^2 হয় । এর কোন তাতপর্্য আছে কি না ?
না, আলাদা কোনো তাৎপর্য নেই। E=mc^2 সমীকরনটা কোনো নির্দিষ্ট পরিমাণ ভর থেকে প্রাপ্য শক্তিই হিসাব করে দেয় কেবল। c এর স্থলে আলোর বেগ নয় এমন কোনো মান বসালে তা ভিত্তিহীন হবে।