তোমরা ইতঃপূর্বে কম্বিনেটরিক্সের হাবিজাবি আলোচনায় বিন্যাস সম্পর্কে প্রাথমিক ধারণা পেয়েছিলে। আমরা আজকে কেবলমাত্র বৃত্তাকার বিন্যাস বা চক্রবিন্যাস নিয়ে আলোচনা করব। মানে কতগুলো লোককে বৃত্তাকার একটি টেবিল এ মোট কতভাবে সাজানো যায় কিংবা কতভাবে একটি মালা তৈরী করা যায় তা দেখব। 😀
একটি বৃত্তাকার টেবিলে তিনটি চেয়ার আছে ধরো প্রত্যেক চেয়ারে ১, ২, ৩ করে নাম্বার দেয়া আছে। এখন যদি প্রশ্ন করি A, B, C এই তিনজন লোক কতভাবে ঐ বৃত্তাকার টেবিলে বসতে পারবে?
অবশ্যই 3! বা 6 ভাবে। নিচের ছবিটি দেখোঃ
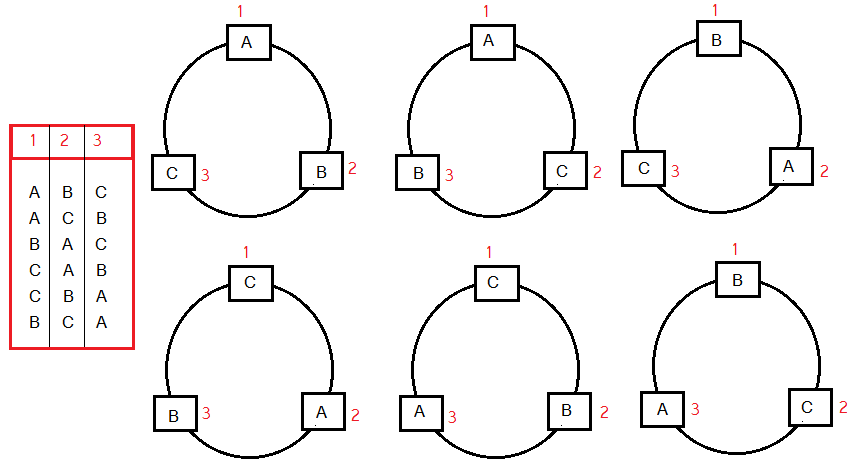
এক্ষেত্রে যেহেতু চেয়ারগুলোতে নাম্বার দেয়া ছিল তাই রৈখিক ও বৃত্তাকার বিন্যাসে কোনো পার্থক্য হয় নি। কারণ প্রত্যেক আলাদা আলাদা চেয়ারগুলোর নাম্বারিং এর জন্যে আলাদা আলাদা বিন্যাস পাওয়া গেছে।
এখন যদি ভাবি যে চেয়ারগুলোতে কোনো নাম্বার দেয়া নেই। মানে চেয়ারগুলো দেখতে নিচের মত:
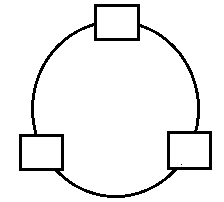
চেয়ারে কোনো নাম্বার দেয়া নেই। এখন যদি প্রশ্ন করি A, B, C এই তিনজন লোক কতভাবে ঐ বৃত্তাকার টেবিলে বসতে পারবে?
তাহলে অবশ্যই ব্যাপারটা আগের মত দাঁড়াচ্ছে না। যেহেতু আমরা চেয়ারে নাম্বারের কথা ভাবছি না, তাহলে কেবলমাত্র A, B, C এই তিনজন লোকের টেবিলে আপেক্ষিক অবস্থান বিবেচনায় আসছে। কে কোন চেয়ারে বসেছে তা শুধুমাত্র আমাদের দেখার দিকের জন্যে ভিন্ন হচ্ছে।
আজ আমাদের আলোচনার বিষয় আসলে সেইটাই। 😀
যখন জিনিসগুলোকে সাজানোর পর উলটানো বা উলটিয়ে দেখা যাবে না (কেবল একদিক দিয়েই দেখা যাবে ):
কত উপায়ে 4 জন লোককে একটি বৃত্তাকার টেবিলে বসানো যাবে? যেখানে কোনো চেয়ারেই নাম্বার দেয়া নেই মানে চেয়ারগুলো দেখতে একরকম।
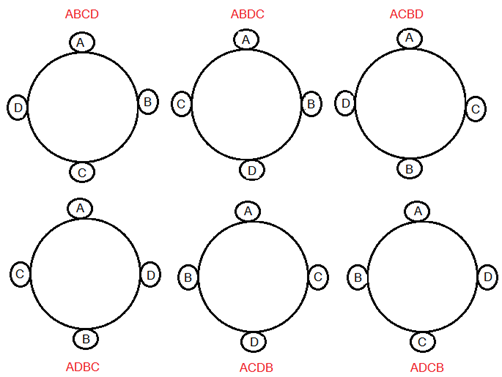
আমরা যে ধরণের বিন্যাস দেখেছিলাম তা ছিল নাম্বারিং করা চেয়ারে বৃত্তাকার বিন্যাস এখন আমরা দেখব নাম্বার ছাড়া দেখতে একরকম চেয়ারে চক্রাকারে বা বৃত্তাকারে বিন্যস্ত করলে বিন্যাস সংখ্যা কেমন হয়। ধরি প্রশ্নের চার জন লোকের নাম A, B, C, D . তাদেরকে একটি গোল টেবিল এ বসালে কি বিন্যাস সংখ্যা আগের মত 4! ই হবে? অবশ্যই না। নিচের ছবিটা দেখোঃ
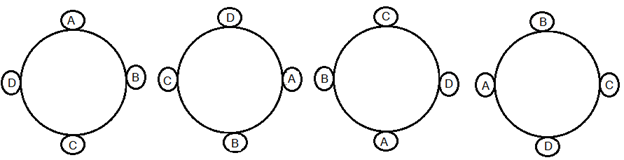
এই বিন্যাসগুলো কি আলাদা আলাদা? না। কারণ আমি যদি সবগুলো বিন্যাস A থেকে শুরু করে ঘড়ির কাঁটার দিকে পড়া শুরু করি তাহলে সবগুলোই ABCD
B থেকে শুরু করে ঘড়ির কাঁটার দিকে পড়া শুরু করি তাহলে সবগুলোই BCDA
D থেকে শুরু করে ঘড়ির কাঁটার বিপরীত দিকে পড়া শুরু করি তাহলে সবগুলোই DCBA ,…… আসলে আমি যেভাবেই পড়ি না কেন সবগুলো আসলে একই বিন্যাস নির্দেশ করছে। কারণ সবগুলো বিন্যাসে এর একজনের সাপেক্ষে আরেকজনের আপেক্ষিক অবস্থান একই আছে। কেবল আমরা টেবিলের ভিন্ন পাশ থেকে দেখছি বলে ভিন্ন দেখাচ্ছে।
একইভাবে
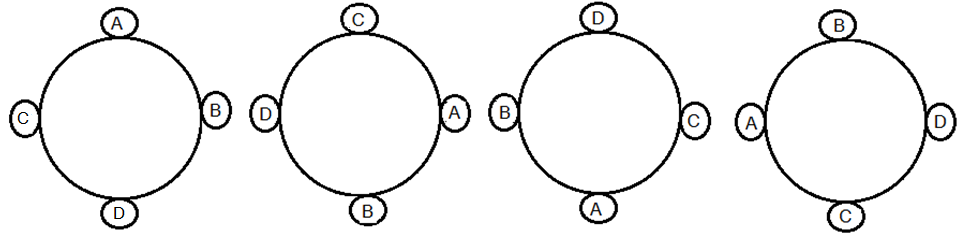
এই বিন্যাসগুলোর সবগুলোই একরকম মানে ABDC .আসলে আমি যেভাবেই পড়ি না কেন সবগুলো আসলে একই বিন্যাস নির্দেশ করছে।
একইভাবে আমরা ACBD, ADBC, ACDB, ADCB এর প্রত্যেকটির জন্যেও চারটি করে একইরকম বিন্যাস পাবো। তাহলে 4! সংখ্যক বিন্যাস হবে এরকম:
| ABCD, DABC, CDAB, BCDA | সবগুলোই ABCD |
| ABDC, CABD, DCAB, BDCA | সবগুলোই ABDC |
| ACBD, DACB, BDAC, CBDA | সবগুলোই ACBD |
| ADBC, CADB, BCAD, DBCA | সবগুলোই ADBC |
| ACDB, BACD, DBAC, CDBA | সবগুলোই ACDB |
| ADCB, BADC, CBAD, DCBA | সবগুলোই ADCB |
তাহলে বিন্যাস অবশ্যই 4! থেকে কিছু কম আসবে।
এখন কি পরিমাণ কম আসবে আর কি পরিমাণই বা আসবে?
এবার একটু সেই ছোটবেলায় করা ঐকিক নিয়ম দিয়ে করে দেখা যাক।
উপরের চেয়ারে নাম্বার দেয়া অবস্থার প্রত্যেক 4 টি বিন্যাসের জন্যে চেয়ারে নাম্বার ছাড়া অবস্থায় বিন্যাস পাওয়া যায় 1 টি
∴চেয়ারে নাম্বার দেয়া অবস্থার প্রত্যেক 1 টি বিন্যাসের জন্যে চেয়ারে নাম্বার ছাড়া অবস্থায় বিন্যাস পাওয়া যাবে 1/4 টি
∴চেয়ারে নাম্বার দেয়া অবস্থার প্রত্যেক 4! টি বিন্যাসের জন্যে চেয়ারে নাম্বার ছাড়া অবস্থায় বিন্যাস পাওয়া যা্বে 4!/4 টি = 3! টি
তার মানে আমরা A, B, C, D এই চারজন লোককে একটি বৃত্তাকার টেবিলে বসাতে পারবো মোট 3! উপায়ে। (যেখানে সবগুলো চেয়ার দেখতে একরকম আর কোনো চেয়ারে নাম্বার দেয়া নেই।)
তাহলে এবার একটু ভিন্নভাবে দেখা যাক ব্যাপারটাকে।
A, B, C, D এই চারজন লোকের যেকোন একজনকে আঠা দিয়ে তার চেয়ারে লাগিয়ে দেই যাতে সে আর নড়তে না পারে মানে চেয়ার ছাড়তে না পারে আরকি। এবার বাকিদেরকে সাজাই। তার মানে আমি এখানে A কে আঠা দিয়ে তার চেয়ারে লাগিয়ে দিয়েছি যাতে সে নড়তে না পারে। 😀 এরপর বাকিদেরকে বিন্যস্ত করেছি। তাহলে কি আর একই বিন্যাস ফিরে আসবে? অবশ্যই না। সবগুলো ভিন্ন হবে আর আমাদের কাঙ্ক্ষিত বিন্যাস পাওয়া যাবে। তার মানে আমরা একজন বাদে বাকি 3 জনকে বিন্যস্ত করছি আর 3 জনকে 3 টি seat এ বিন্যস্ত করা যায় 3! উপায়ে অর্থাৎ আমাদের নির্ণেয় বিন্যাস 3! বা (4-1)! । বিন্যাসগুলো হলঃ
যখন n সংখ্যক জিনিসগুলোকে সাজানোর পর উলটানো বা উলটিয়ে দেখা যাবে না (মানে কেবল একদিক থেকেই দেখা যাবে) তখন ঐ n সংখ্যক জিনিস নিয়ে চক্রবিন্যাস বা বৃত্তাকার বিন্যাস হবে (n-1)!
n সংখ্যক জিনিসের বৃত্তাকারে সাজানোর ক্ষেত্রে,
n সংখ্যক rotational symmetry এর জন্যে পাওয়া যাবে মাত্র 1 টি বিন্যাস
∴ 1 সংখ্যক এর জন্যে বিন্যাস পাওয়া যাবে 1/n টি
∴ n! সংখ্যক এর জন্যে বিন্যাস পাওয়া যাবে n!/n বা (n-1)! গুলো
আচ্ছা, এবার যদি বলি, 4 জন লোক আছে, তাদেরকে কতভাবে তিনটি চেয়ার বিশিষ্ট একটি বৃত্তাকার টেবিলে বসানো যাবে? যেখানে কোনো চেয়ারেই নাম্বার দেয়া নেই মানে চেয়ারগুলো দেখতে একরকম।
আগের মতই ধরি, প্রশ্নের চার জন লোকের নাম A, B, C, D . তাদের থেকে যেকোনো তিনজনকে নিয়ে ঐ বৃত্তাকার টেবিল এ বসাতে হবে।
প্রথমে একটু সহজভাবে ভাবা যাক। আমাদের কাজ দুটো। প্রথমে 4 জন থেকে 3 জন নিতে হবে। তারপর ঐ 3 জনকে বৃত্তাকার টেবিলে বসিয়ে বিন্যস্ত করতে হবে।
এখন, 4 জন থেকে 3 জন বাছাই করা যায় 4C3 উপায়ে আর 3 জনকে বৃত্তাকার টেবিলে বসানো যায় 2! উপায়ে। প্রত্যেক বাছাইয়ের জন্যে 2! উপায়ে বৃত্তাকার টেবিলে বসানো যায়। তাহলে বৃত্তাকার টেবিলে মোট বসানো যাবে 4C3 × 2! উপায়ে। 😀
এবার একটু অন্যভাবে ভাবা যাক আগের মত আমরা খুঁজে বের করব কতগুলো একই রকম বিন্যাস পাওয়া যায়।
যদি চেয়ারগুলোতে নাম্বার দেয়া থাকতো তাহলে 4 জন থেকে যেকোনো 3 জনকে নিয়ে ঐ বৃত্তাকার টেবিল এ বসানো যাবে 4P3 উপায়ে। তাহলে 4P3 সংখ্যক বিন্যাস হবে এরকম:
| ABC, CAB, BCA | সবগুলোই ABC | ABD, DAB, BDA | সবগুলোই ABD |
| ACD, DAC, CDA | সবগুলোই ACD | ACB, BAC, CBA | সবগুলোই ACB |
| BCD, DBC, CDB | সবগুলোই BCD | ADB, BAD, DBA | সবগুলোই ADB |
| BDC, CBD, DCB | সবগুলোই BDC | ADC, CAD, DCA | সবগুলোই ADC |
নিচের ছবিটি দেখো:
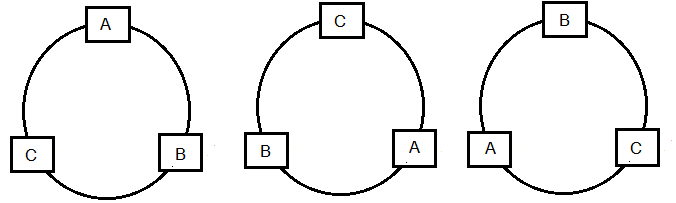 এই বিন্যাসগুলোর সবগুলোই একরকম মানে ABC .আসলে আমি যেভাবেই পড়ি না কেন সবগুলো আসলে একই বিন্যাস নির্দেশ করছে।
এই বিন্যাসগুলোর সবগুলোই একরকম মানে ABC .আসলে আমি যেভাবেই পড়ি না কেন সবগুলো আসলে একই বিন্যাস নির্দেশ করছে।
একইভাবে আমরা ACD, ADB, ACB, BDC,……… এর প্রত্যেকটির জন্যেও তিনটি করে একইরকম বিন্যাস পাবো।
তাহলে বিন্যাস অবশ্যই 4P3 থেকে কিছু কম আসবে।
উপরের চেয়ারে নাম্বার দেয়া অবস্থার প্রত্যেক 3 টি বিন্যাসের জন্যে চেয়ারে নাম্বার ছাড়া অবস্থায় বিন্যাস পাওয়া যায় 1 টি
∴চেয়ারে নাম্বার দেয়া অবস্থার প্রত্যেক 1 টি বিন্যাসের জন্যে চেয়ারে নাম্বার ছাড়া অবস্থায় বিন্যাস পাওয়া যাবে 1/3 টি
∴চেয়ারে নাম্বার দেয়া অবস্থার প্রত্যেক 4P3 টি বিন্যাসের জন্যে চেয়ারে নাম্বার ছাড়া অবস্থায় বিন্যাস পাওয়া যা্বে 4P3/3 টি
বা এভাবেও বলা যায়,
3 সংখ্যক rotational symmetry এর জন্যে পাওয়া যাবে মাত্র 1 টি বিন্যাস
∴ 1 সংখ্যক এর জন্যে বিন্যাস পাওয়া যাবে 1/3 টি
∴4P3 সংখ্যক এর জন্যে বিন্যাস পাওয়া যাবে 4P3/3 গুলো।
যখন n সংখ্যক জিনিসগুলো থেকে r সংখ্যক নিয়ে সাজানোর পর উলটানো বা উলটিয়ে দেখা যাবে না (মানে কেবল একদিক থেকেই দেখা যাবে) তখন ঐ n সংখ্যক জিনিস থেকে r সংখ্যক নিয়ে চক্রবিন্যাস বা বৃত্তাকার বিন্যাস হবে nPr /r বা nCr × (r-1)!
n সংখ্যক জিনিস থেকে r সংখ্যক নিয়ে বৃত্তাকারে সাজানোর ক্ষেত্রে,
r সংখ্যক rotational symmetry এর জন্যে পাওয়া যাবে মাত্র 1 টি বিন্যাস
∴ 1 সংখ্যক এর জন্যে বিন্যাস পাওয়া যাবে 1/r টি
∴ nPr সংখ্যক এর জন্যে বিন্যাস পাওয়া যাবে nPr /r গুলো।
অথবা
n সংখ্যক জিনিস থেকে r সংখ্যক জিনিস বাছাই করা যায় nCr উপায়ে।
এখন যেকোনো 1 টি বাছাই এর জন্যে r সংখ্যক জিনিসকে বৃত্তাকারে সাজানো যায় (r-1)! উপায়ে।
∴ nCr সংখ্যক বাছাই এর জন্যে r সংখ্যক জিনিসকে বৃত্তাকারে সাজানো যায় nCr × (r-1)! উপায়ে।
যখন জিনিসগুলোকে সাজানোর পর উলটানো বা উলটিয়ে দেখা যাবে (মানে দুইদিক থেকেও দেখা যাবে) :
এবার আরেকটি প্রশ্ন করি, কত উপায়ে 4 টি ভিন্ন রঙের মুক্তাকে একটি বৃত্তাকার মালায় বসানো যাবে?
এবার কি আগের মত 3! হবে? না। কারণ আমরা মালাটিকে দুইপাশ থেকে দেখতে পারি বা সহজ কথায় তুমি মালাটি ধরে আয়নার সামনে দাঁড়িয়ে আছো। তাহলে কিন্তু একই মালাকে দুইরকম দেখবে বাস্তবে তুমি একরকম দেখছো আর তোমার বিম্বে আরেক রকম। ধর, মালায় গাঁথার জন্যে একটি লাল (R) , একটি নীল (B), একটি সবুজ (G) আর একটি গোলাপী (P) মুক্তা আছে। নিচের ছবিটি দেখোঃ
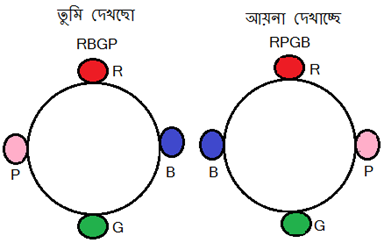
তার মানে এবার মালার এক ধরণের সাজনো অবস্থার জন্যে আমরা আগের বারের দুইটি করে বিন্যাস পেয়ে যাচ্ছি। তার মানে এবার বিন্যাস আগের বারের চেয়ে আরও কম পাবো। কারণ আগেরবার বৃত্তাকারের ক্ষেত্রে যেখানে 2 টি বিন্যাস পেয়েছিলাম সেখানে এবার 1 টি করে বিন্যাস পাচ্ছি। তার মানে এবার বিন্যাস সংখ্যা আগেরবারের অর্ধেক হয়ে যাবে মানে 4 টি ভিন্ন রঙের মুক্তাকে একটি বৃত্তাকার মালায় বসানো যাবে 3!/2 উপায়ে।
আগের 2 টি বিন্যাসের জন্যে এখন বিন্যাস পাচ্ছি 1 টি
∴ আগের 1 টি বিন্যাসের জন্যে এখন বিন্যাস পাচ্ছি 1/2 টি
∴ আগের (n-1)! বিন্যাসের জন্যে এখন বিন্যাস পাচ্ছি (n-1)!/2 টি
যখন n সংখ্যক জিনিসগুলোকে সাজানোর পর উলটানো বা উলটিয়ে দেখা যাবে (অর্থাৎ দুইপাশ থেকে দেখা যাবে) তখন ঐ n সংখ্যক জিনিস নিয়ে চক্রবিন্যাস বা বৃত্তাকার বিন্যাস হবে (n-1)!/2
n সংখ্যক rotational symmetry এর প্রত্যেকটির জন্যে 2 টি করে line symmetry পাওয়া যায় তাই মোট 2n সংখ্যক symmetry পাওয়া যায় যাদের জন্যে মাত্র একটি বিন্যাস পাওয়া যায় তাই বিন্যাস সংখ্যা হয় n!/(2n) বা (n-1)!/2
আচ্ছা আবার যদি আগেরবারের মত বলি,
কত উপায়ে 4 টি ভিন্ন রঙের মুক্তা থেকে 3 টি নিয়ে একটি বৃত্তাকার মালায় বসানো যাবে?
তাহলে আগেরবারের মত দুইভাবে বলা যায়।
প্রথমে আমরা যদি এভাবে বলি, আমাদের কাজ এবারও দুটো। 4 টি ভিন্ন রঙের মুক্তা থেকে 3 টি বাছাই করা এবং সেগুলো নিয়ে বৃত্তাকার মালা বানানো।
এখন, 4 টি থেকে 3 টি বাছাই করা যায় 4C3 উপায়ে আর 3 টিকে বৃত্তাকার মালায় বসানো যায় 2!/2 উপায়ে। প্রত্যেক বাছাইয়ের জন্যে 2!/2 উপায়ে বৃত্তাকার মালায় বসানো যায়। তাহলে বৃত্তাকার মালায় মোট বসানো যাবে 4C3 × (2!/2) উপায়ে। কি, হয়ে গেলো না? 😀
এবার একটু অন্যভাবে ভাবা যাক আগের মত আমরা খুঁজে বের করব বৃত্তাকার বিন্যাসের মধ্যে কতগুলো একই রকম বিন্যাস পাওয়া যায়।
যদি মুক্তাগুলোকে উল্টিয়ে দেখা না যেত তাহলে 4 টি ভিন্ন রঙের মুক্তা থেকে 3 টি নিয়ে একটি বৃত্তাকার মালায় বসানো যেত 4P3/3
কিন্তু যেহেতু মুক্তাগুলোকে দুইপাশ থেকে দেখা যায় তাহলে প্রত্যেকটি বৃত্তাকার বিন্যাসের জন্যে আবার 2 টি করে একইরকম বিন্যাস পাওয়া যাবে।
তাহলে
আগে যেখানে বৃত্তাকার বিন্যাসের ক্ষেত্রে, 2 টি বিন্যাস পেতাম সেখানে এখন বিন্যাস পাচ্ছি 1 টি
∴ আগের 1 টি বিন্যাসের জন্যে এখন বিন্যাস পাচ্ছি 1/2 টি
∴ আগের 4P3/3 বিন্যাসের জন্যে এখন বিন্যাস পাচ্ছি (4P3/3) /2 টি = 4P3/(3×2)
যখন n সংখ্যক জিনিসগুলো থেকে r সংখ্যক নিয়ে সাজানোর পর উলটানো বা উলটিয়ে দেখা যাবে (অর্থাৎ দুইপাশ থেকে দেখা যাবে) তখন ঐ n সংখ্যক জিনিস থেকে r সংখ্যক নিয়ে চক্রবিন্যাস বা বৃত্তাকার বিন্যাস হবে nPr /2r
n সংখ্যক জিনিসগুলো থেকে r সংখ্যক নিয়ে সাজানোর ক্ষেত্রে r সংখ্যক rotational symmetry এর প্রত্যেকটির জন্যে 2 টি করে line symmetry পাওয়া যায় তাই মোট 2r সংখ্যক symmetry পাওয়া যায় যাদের জন্যে মাত্র একটি বিন্যাস পাওয়া যায় তাই বিন্যাস সংখ্যা হয় nPr/(2r) বা
nCr × ( (r-1)!/2 )
এবার কিছু উদাহারণ দেখা যাক। 😀
উদাহারণ-১ঃ
কত উপায়ে 5 জন বালক আর 3 জন বালিকাকে একটি বৃত্তাকার টেবিলে বসানো যাবে যাতে –
i) সবাই যেভাবে ইচ্ছা বসতে পারে?
ii) ১ম বালক আর ১ম বালিকা যাতে কখনই পাশাপাশি না বসে?
iii) কোনো বালিকাই যাতে পাশাপাশি না থাকে?
সমাধান:
i) 5 জন বালক আর 3 জন বালিকার অর্থাৎ (5+3) = 8 জন সবাই যেভাবে ইচ্ছা বসতে পারে। তাহলে এই 8 জনকে বৃত্তাকার টেবিলে বসানো যায় (8-1)! = 7! উপায়ে।
ii) ধরি, ১ম বালকের নাম B1 আর ১ম বালিকার নাম G1 তাহলে এই দুইজনকে পাশাপাশি রাখা যাবে না। তাহলে এক কাজ করি ১ম বালক B1 কে আমরা প্রথমে দূরে দাঁড় করিয়ে রাখি। বাকি সবাইকে বসিয়ে দেই। আর বাকি (4+3)=7 জন সবাইকে বৃত্তাকার টেবিলে বসানো যায় (7-1)!=6! উপায়ে। এখন এই 7 জনের প্রত্যকের পাশে টি করে টেবিলে মোট ফাঁকা জায়গা আছে 7 টি। এর মধ্যে ১ম বালিকা G1 এর দুইপাশে জায়গা আছে 2 টি। তাহলে ১ম বালক B1 কে বসানোর জন্যে জায়গা আছে (7-2)= 5 টি।
নিচের ছবিটি দেখো (যেকোনো একভাবে বসানোর জন্যে): সবুজ জায়গাগুলোতে B1 কে বসানো যাবে।
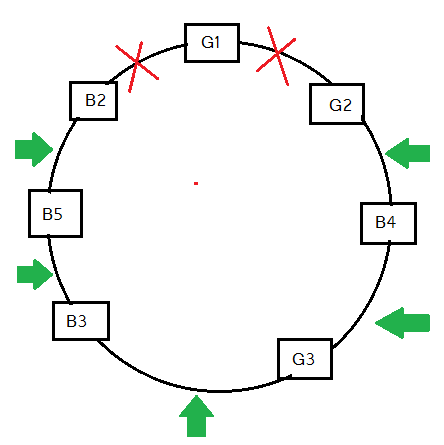
আর এই 5 জায়গায় ১ম বালক B1 কে বসানো যায় 5 ভাবে। অর্থাৎ বৃত্তাকার টেবিলে যাতে ১ম বালক আর ১ম বালিকা কখনই পাশাপাশি না বসে এমনভাবে বসানো যেতে পারে মোট (6! × 5) উপায়ে।
আরেকভাবেও ভাবা যেতে পারে, আমরা যদি B1 আর G1 একত্রে থাকবে বা পাশাপাশি থাকবে এমন বিন্যাসগুলো বের করতে পারি তাহলে মোট বিন্যাস থেকে সেগুলো বাদ দিলেই তো B1 আর G1 পাশাপাশি থাকবে না এমন বিন্যাসগুলো পাওয়া যাবে।
তাহলে (5+3)=8 জনকে মোট বৃত্তাকার টেবিলে বসানো যেতে পারে (8-1)! = 7! উপায়ে।
আমরা এবার B1 আর G1 একত্রে থাকবে বা পাশাপাশি থাকবে এমন বিন্যাসগুলো নির্ণয় করবো। একটা কাজ করি B1 আর G1 কে একটা প্যাকেটের মধ্যে ভরে ফেলি। যাতে তারা প্যাকেটের মধ্যে নড়াচড়া করতে পারলেও প্যাকেটের বাইরে আসতে না পারে। এবার ঐ প্যাকেট শুদ্ধ নিয়ে সাজানো শুরু করি। তাহলে মোট লোক পাওয়া গেলো ( 4 জন বালক+ 2 জন বালিকা+ 1 টি প্যাকেট) = 7 জন। আর এই 7 জনকে মোট বৃত্তাকার টেবিলে বসানো যেতে পারে (7-1)! = 6! উপায়ে। আবার, B1 আর G1 নিজেদের মধ্যে প্যাকেটের ভিতরে বিন্যস্ত হতে পারে 2! উপায়ে। তাহলে B1 আর G1 একত্রে থাকবে বা পাশাপাশি থাকবে এমনভাবে টেবিলে বসানো যাবে (6! × 2!) উপায়ে।
তাহলে B1 আর G1 একত্রে থাকবে না বা পাশাপাশি থাকবে না এমনভাবে টেবিলে বসানো যাবে = মোট বিন্যাস – একত্রে থাকবে বা পাশাপাশি থাকবে এমন বিন্যাস
অর্থাৎ B1 আর G1 একত্রে থাকবে না বা পাশাপাশি থাকবে না এমনভাবে টেবিলে বসানো যাবে 7! – (6! × 2!) উপায়ে।
iii) এবার এক কাজ করি প্রথমেই বালকগুলোকে বসিয়ে দেই কারণ যেহেতু তাদের বসানোর উপর কোনো শর্ত নেই।
আর 5 জন বালককে বৃত্তাকার টেবিলে বসানো যায় (5-1)! = 4! উপায়ে।
নিচের ছবিটি দেখো (যেকোনো একভাবে বসানো অবস্থায় বালকদের জন্যে):
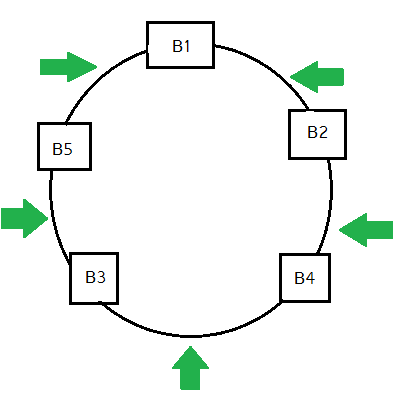
তাহলে ঐ সবুজ জায়গুলোতে বালিকাদেরকে বসানো যাবে। আর 5 টি জায়গায় 3 জন বালিকাকে বসানো যাবে 5P3 উপায়ে।
অর্থাৎ কোনো বালিকাই যাতে পাশাপাশি না থাকে এমন শর্তে 5 জন বালক আর 3 জন বালিকাকে একটি বৃত্তাকার টেবিলে বসানো যাবে ( 4! × 5P3 ) উপায়ে।
উদাহারণ-২ঃ
কত উপায়ে 2n জন দম্পতিকে ( n জন স্বামী এবং n জন স্ত্রী ) একটি বৃত্তাকার টেবিলে বসানো যাবে যাতে –
i) সবাই যেভাবে ইচ্ছা বসতে পারে?
ii) কোনো দুইজন মহিলা পাশাপাশি না থাকে?
iii) প্রত্যেক মহিলা তার স্বামী এর সাথে বসে?
সমাধান:
i) 2n জন দম্পতির সবাই একটি বৃত্তাকার টেবিলে যেভাবে ইচ্ছা বসতে পারে। তাহলে এই 2n জনকে বৃত্তাকার টেবিলে বসানো যায় (2n – 1)! উপায়ে।
ii) এবার এক কাজ করি প্রথমেই স্বামী গুলোকে বসিয়ে দেই কারণ যেহেতু তাদের বসানোর উপর কোনো শর্ত নেই।
আর n জন পুরুষকে বৃত্তাকার টেবিলে বসানো যায় (n – 1)! উপায়ে। এবার আগের উদাহারণটির মত প্রত্যেক পুরুষের পাশে জায়গা আছে 1 টি করে মোট n টি, এই n সংখ্যক জায়গায় সংখ্যক মহিলাকে বসানো যায় n! উপায়ে।
তাহলে, 2n জন দম্পতিকে ( n জন স্বামী এবং n জন স্ত্রী) একটি বৃত্তাকার টেবিলে বসানো যাবে যাতে কোনো দুইজন মহিলা পাশাপাশি না থাকে (n – 1)! × n! উপায়ে।
iii) প্রত্যেক মহিলাকে তার স্বামীর সাথে বসাতে হবে।
আমরা একটা কাজ করি তাহলে প্রত্যেক স্বামী ও স্ত্রী মানে দম্পতিকে একটি করে আলাদা আলাদা প্যাকেটের মধ্যে ভরে ফেলি। তাহলে প্যাকেট পাওয়া যাবে কতগুলো? অবশ্যই n গুলো।
এবার এই n সংখ্যক প্যাকেটগুলোকে আমরা বৃত্তাকার টেবিলে বসাতে পারি (n – 1)! উপায়ে। এখন প্রত্যেক প্যাকেটের মধ্যে প্রত্যেক দম্পতি নিজেদের মধ্যে বিন্যস্ত হতে পারে 2! উপায়ে।
এখন প্যাকেটগুলোর একটি সাজানো অবস্থার জন্যে সব দম্পতি নিজেদের মধ্যে বিন্যস্ত হতে পারে (2! × 2! × 2! × 2! × ……. × 2! × 2!) উপায়ে ( n সংখ্যক 2! ) অর্থাৎ (2!)n উপায়ে।
তাহলে প্রত্যেক মহিলা তার স্বামী এর সাথে বসে এমন শর্তে 2n জন দম্পতিকে ( n জন স্বামী এবং n জন স্ত্রী ) একটি বৃত্তাকার টেবিলে বসানো যাবে (n – 1)! × (2!)n উপায়ে।
উদাহারণ-৩ঃ
কত উপায়ে 3 জন পুরুষ আর 3 জন মহিলা কে একটি বৃত্তাকার টেবিলে বসানো যাবে-
i) প্রত্যেক মহিলা দুইজন পুরুষের মাঝে থাকে?
ii) দুইজন নির্দিষ্ট মহিলা একত্রে থাকে?
iii) দুইজন নির্দিষ্ট মহিলা একত্রে না থাকে?
iv) সব মহিলা একত্রে থাকে?
v) দুইজন নির্দিষ্ট মহিলার মাঝে যাতে কেবল একজন লোকই থাকে?
সমাধান:
i) প্রথমে পুরুষদেরকে বৃত্তাকার টেবিলে বসিয়ে দেই তাদের বসানো যাবে (3-1)! বা 2! উপায়ে।এবার প্রত্যেক পুরুষের পাশে একটি করে মোট 3 টি ফাঁকা জায়গায় মহিলা 3 জনকে বসানো যায় 3! উপায়ে। তাহলে প্রত্যেক মহিলা দুইজন পুরুষের মাঝে থাকে এমনভাবে বৃত্তাকার টেবিলে বসানো যাবে 2! × 3! উপায়ে
ii) আগের মতই যারা একত্রে থাকবে তাদের একটি প্যাকেট বিবেচনা করলে উপাদান সংখ্যা হয় 4 টি + 1 টি প্যাকেট মানে 5 টি । এখন এই 5 জনকে বৃত্তাকার টেবিলে বসানো যায় 4! উপায়ে এবং ঐ দুই মহিলা নিজেদের মধ্যে বিন্যস্ত হতে পারে 2! উপায়ে। দুইজন নির্দিষ্ট মহিলা একত্রে থাকে এমন বিন্যাস সংখ্যা হবে 2! × 4!
iii) দুইজন নির্দিষ্ট মহিলা একত্রে না থাকে এমন বিন্যাস = মোট বিন্যাস – দুইজন নির্দিষ্ট মহিলা একত্রে থাকে এমন বিন্যাস
অর্থাৎ দুইজন নির্দিষ্ট মহিলা একত্রে না থাকে এমন বিন্যাস = 5! – 2! × 4!
iv) যারা একত্রে থাকবে তাদের একটি প্যাকেট বিবেচনা করলে উপাদান সংখ্যা হয় 3 টি + 1 টি প্যাকেট মানে 4 টি । এখন এই 4 জনকে বৃত্তাকার টেবিলে বসানো যায় 3! উপায়ে এবং ঐ তিন মহিলা নিজেদের মধ্যে বিন্যস্ত হতে পারে 3! উপায়ে। সব মহিলা একত্রে থাকে এমন বিন্যাস সংখ্যা হবে 3! × 3!
v) দুইজন নির্দিষ্ট মহিলার মাঝে যাতে কেবল একজন লোকই থাকে মানে যাতে ঐ দুইজন মহিলা পাশাপাশি না থাকে এবং মাঝে একজন দিয়ে আলাদা থাকে। তাহলে আগে বাকি 4 জনকে বসিয়ে দেই। তাদের বৃত্তাকার টেবিলে বসানো যাবে 3! উপায়ে।এবার প্রত্যেকের পাশে একটি করে মোট 4 টি ফাঁকা জায়গা আছে। এখন একজন মহিলাকে বসানো যায় 4 টি ফাঁকা জায়গার যেকোন একটিতে। একজন মহিলাকে বসালেই ২য় মহিলার আসন নির্দিষ্ট হয়ে যাবে কারণ তাকে ঐ মহিলার ঠিক একজন পাশেই বসতে হবে। আবার দুইজন মহিলা নিজেদের মধ্যে বিন্যস্ত হতে পারে 2! উপায়ে। দুইজন নির্দিষ্ট মহিলার মাঝে যাতে কেবল একজন লোকই থাকে এমন বিন্যাস সংখ্যা হবে 3! × 4 × 2!
আশা করি তোমরা ব্যাপারগুলো বুঝতে পেরেছো। আজ তাহলে এ পর্যন্তই। সবার শিক্ষার শুরুটা হোক মাতৃভাষাতেই -এই শুভকামনায় শেষ করছি। আর হ্যাঁ, কোনো কিছু না বুঝতে পারলে অবশ্যই জানাবে কিন্তু । আর সেই সাথে এই ( চক্র-বিন্যাস ও মালাবাহার ) লেখাটিও দেখতে পারো। 😀 😀

Thanks 🙂
Very much helpful