সরলরৈখিক বিন্যাসের ক্ষেত্রে আমরা দেখি, n সংখ্যক বস্তুকে সাজানো যায় (বিন্যস্ত করা) n! উপায়ে। কিন্তু চক্রাকার বিন্যাসের ক্ষেত্রে, একই n সংখ্যক বস্তু যখন চক্রাকারে অবস্থান নেয় তখন তাদের সাজানোর উপায় সংখ্যা (n-1)! এবং কিছু কিছু ক্ষেত্রে (যেমন: মুক্তোর মালা) সাজানোর উপায় সংখ্যা (n-1)!/2 । এরকম বৈষম্য কেন হয়? আসুন দেখা যাক, প্রথমে আমরা যৌক্তিকভাবে এবং পরে গাণিতিকভাবে বিশ্লেষণ করব,
ধরি একটি সুখী পরিবারের ৪ সদস্য একটা গোলটেবিলের চারপাশে চক্রাকারে বসেছে (চিত্রের মত)।

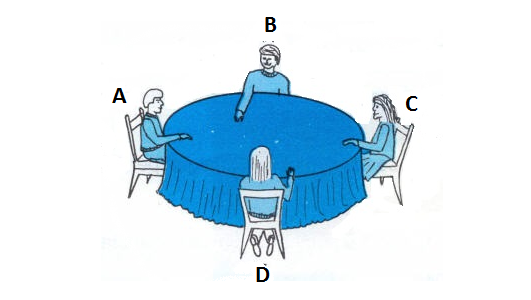
একটু পর সবাই নিজ নিজ চেয়ার ছেড়ে দিয়ে নিজের ঠিক বাঁপাশের চেয়ারে গিয়ে বসল (অর্থাৎ সবাই anti-clock-wise জায়গা বদলাল) , এবং একই কাজ আরও দুই বার করল ( মোট ৩ বার জায়গা পরিবর্তন করল)।

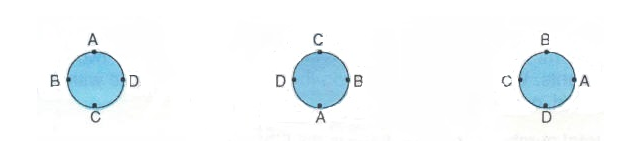
আচ্ছা বলুন তো তাদের এই ৪ টা ভিন্ন ভিন্ন বসার চিত্রকল্পের ক্ষেত্রে কি আমরা ৪ টা ভিন্ন ভিন্ন বিন্যাস পাচ্ছি? সরলরৈখিক বিন্যাসের ক্ষেত্রে কিন্তু পাওয়ার কথা, কিন্তু এখানে সে নিয়ম খাটবে না। এখানে এই ৪ টা আপাতদৃষ্টিতে দেখতে ভিন্ন ভিন্ন বিন্যাস আসলে একটাই বিন্যাস নির্দেশ করে। ভালমত খেয়াল করে দেখি, ৪ টা কেস এই প্রত্যেকের আপেক্ষিক অবস্থান একই আছে; অর্থাৎ সব ক্ষেত্রেই A এর ডান পাশে B, তার ডান পাশে C, তার ডান পাশে D বসেছে। বিন্যাস বলতে বুঝি ক্রম’র (sequence) তারতম্য , সেই ক্রম কিন্তু এখানে ৪ টা কেস এই একই আছে। তার মানে এই ৪ টা ভিন্ন ভিন্ন কেস কে আলাদা বিন্যাস গণ্য করা যাবে না; তারা একটি বিন্যাসেরই প্রতিচ্ছবি।
তাহলে সমস্যা তৈরি হচ্ছে ৪ জনের একই সাথে জায়গা পরিবর্তন (নিজের জায়গা ছেড়ে পাশের জায়গায়) এর কারণে, ফলে তাদের ক্রম আগের মত থাকার পরেও আমরা কিছুটা বিভ্রান্ত হচ্ছি। এই বিভ্রান্তি দূর করার জন্য আমরা এমন কিছু করব যাতে সবাই একসাথে জায়গা বদলাতে না পারে। এটা করা যায় যেকোন একজনকে তার নিজের জায়গায় চেপে ধরে , যাতে চেয়ার ছেড়ে উঠতে না পারে 😀 । এবং তাকে আটকিয়ে রেখেই আমরা দেখব বাকি সবাই কত ভাবে নিজেদের জায়গা বদলাতে পারে, এবং এক্ষেত্রে আমাদের বলির পাঁঠা হল A (চিত্র)। A স্থির থাকার কারণে বাকি ৩ জন নিজেদের মধ্যে বিন্যস্ত হতে পারে 3!=6 উপায়ে [(4-1)! =3!] (চিত্র)

অর্থাৎ n সংখ্যক এর ক্ষেত্রে আমরা একজনকে স্থির (বলির পাঁঠা) রেখে বাকি (n-1) জনকে (n-1)! উপায়ে বিন্যস্ত করতে পারি। এই হল যৌক্তিক প্রমাণ।
এবার দেখা যাক গাণিতিক প্রমাণ,
আবার ৪ জনের কেস। এবার একবার তাদের গোলটেবিলে আরেকবার তাদের সরলরৈখিক বেঞ্চে বসানো হল। রৈখিক ভাবে বসানো অবস্থায় তাদের এই ৪ টি ক্রম (ABCD,DABC,CDAB,BCDA) ৪ টি ভিন্ন বিন্যাস গঠন করে ( কারণ তাদের আপেক্ষিক অবস্থান আলাদা)। চিত্র,

কিন্তু ঐ একই ৪ জন যখন চক্রাকারে বসে আগের ৪ টি ক্রম (ABCD,DABC,CDAB,BCDA) গঠন করে তখন কিন্তু তা ১ টি বিন্যাস ই নির্দেশ করে।

কারণ, চক্রাকার ৪ টি কেস এ খেয়াল করলে দেখা যাবে তাদের আপেক্ষিক অবস্থান (কার কোন পাশে কে) একই আছে। এবং এই ঘটনা শুধু ৪ জনের জন্য না , n জনের জন্যও প্রযোজ্য হবে। তাহলে ঐকিক নিয়ম অনুসারে,
রৈখিক বিন্যাস n টি হলে চক্র বিন্যাস 1 টি
রৈখিক বিন্যাস 1 টি হলে চক্র বিন্যাস 1/n টি
রৈখিক বিন্যাস n! টি হলে চক্র বিন্যাস n!/n টি      [ n সংখ্যকের জন্য মোট রৈখিক বিন্যাস n!]
=(n-1)! টি।
এবার দেখি বিশেষ ক্ষেত্র, মুক্তোর মালার ক্ষেত্রে মোট বিন্যাস কেন ২ দিয়ে ভাগ করতে হয়।
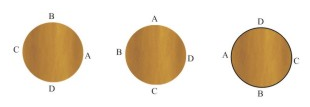
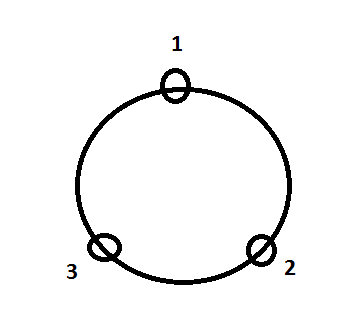
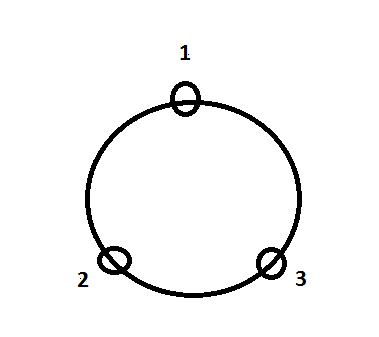
ধরি, একটা মুক্তোর মালা যাতে ৩টি মুক্তো আছে। তো প্রথমে আমরা 123 এই ক্রমে (clock-wise) মালা গাঁথলাম (চিত্র-১)।

এবার খুব ভাল করে খেয়াল করে দেখি, এরকম যে কোন একটি বিন্যাসে মালা গাঁথলে স্বয়ংক্রিয় ভাবে অন্য আরেকটি বিন্যাস তৈরি হয়ে যায়। কীভাবে? আমরা আমাদের গাঁথা মালা (123) এবার পুরোপুরি উল্টিয়ে ধরি অথবা প্রথমবার উপর থেকে দেখলে এবার নিচে থেকে দেখি, কী দেখতে পাব ? ঠিক চিত্র-২ এর মত না? এবং এটা আরেকটা নতুন বিন্যাস না (132 ক্রম এর)?

তার মানে আমরা শুধু 123 ক্রমে একবার মালা গাঁথলাম, কিন্তু পেয়ে গেলাম ২ টা বিন্যাস। তাহলে এবার কি আমাদের সম্ভাব্য সব বিন্যাস পেতে (n-1)! উপায়ে সাজাতে হবে মুক্তো? একদমই না, আমরা তো একভাবে সাজিয়ে ২ টা ভিন্ন বিন্যাস পাচ্ছি। তাহলে এক্ষেত্রে আমরা ঠিক অর্ধেক বার (n-1)!/2 সাজিয়েই সম্ভাব্য সকল বিন্যাস পেয়ে যাব; ঠিক এক ঢিলে দুই পাখি মারার মত।
তাহলে শেষ প্রশ্ন হল, কখন ১ ঢিলে ২ পাখি মরবে, আর কখন ১ ঢিলে ১টাই পাখি মরবে ( অর্থাৎ কখন (n-1)! হবে আর কখন (n-1)!/2 হবে)? আরে, এর উত্তরই তো এতক্ষন ব্যাখ্যা করলাম। তাও সহজে মনে রাখার জন্য,
যেসব ক্ষেত্রে আমরা সাজানোর মাঝখানে উল্টিয়ে পাল্টিয়ে দেখতে পারব কিংবা ঘটনাকে উপর থেকে এবং নিচ থেকে পৃথকভাবে দেখতে পারব (যেমন গহনা, মালা ইত্যাদি), সেসব ক্ষেত্রে উল্টানোর কারণে আমরা অর্ধেক বার সাজিয়েই সবগুলো বিন্যাস পেয়ে যাব; মানে এই সূত্র : (n-1)!/2 । আর যে সকল ক্ষেত্রে আমরা ইচ্ছেমত উল্টিয়ে-পাল্টিয়ে দেখতে পারব না কিংবা শুধু উপর থেকে কিংবা শুধু নিচ থেকে দেখা যাবে ( যেমন, গোল হয়ে বসা একদল মানুষ, এদেরকে আমরা উল্টিয়ে-পাল্টিয়ে দেখতে পারিনা, শুধু উপর থেকেই দেখতে পারি; নিচ থেকে দেখার জন্য মাটির নিচ থেকে দেখতে হবে, তা নিশ্চয়ই করব না 🙂 ) সে সব ক্ষেত্রে এই সূত্র : (n-1)! ।  আচ্ছা তাহলে বলুন তো, সবগুলো মুক্তো একইরকম হলে কোন সুত্র হবে?
বিন্যাস-সমাবেশের ক্ষেত্রে পুরো সমস্যাটা কল্পনা করতে পারলে সমাধান করা খুবই সহজ; তাই আমরা সব সমস্যা শুধু সূত্রে বসিয়ে না করে, একটু ডায়াগ্রাম এঁকে বুঝে বুঝে নতুন নতুন ভাবে করতে চেষ্টা করব। চেষ্টা করব সূত্র মুখস্ত না করে ভালমত বোঝার, সবচেয়ে ভাল হয় যদি আমরা সূত্র অনুভব (feel) করতে পারি। আজকে এই পর্যন্তই, সামনে আমরা বিন্যাস সমাবেশের আরও কিছু মৌলিক বিষয় নিয়ে আলোচনা হবে, থাকবে দ্বিপদী উপপাদ্যে সমাবেশ আসল কীভাবে? এবং আরও কিছু মজার সমস্যা নিয়ে…

কৃতজ্ঞতা:

• সালাউদ্দিন আহমেদ

• Bio
• Latest Posts

Asadullah Hill Galib

Dream big and dare to fail ...

Latest posts by Asadullah Hill Galib (see all)

• ইম্পোস্টার সিনড্রোম - June 11, 2017
• কেন্দ্রমুখী ও কেন্দ্রবিমুখী বল (মিসকনসেপশন) - June 5, 2017
• রিভার্স সাইকোলজি - May 26, 2017