আগের পর্ব : আধুনিক পদার্থবিদ্যা ৩ : কম্পটন ইফেক্ট
কথিত আছে, একদিন হাইজেনবার্গ রাস্তায় সেইইই স্পিডে গাড়ি চালাচ্ছিলেন। পথিমধ্যে এক পুলিশ তাকে থামাল এবং জিজ্ঞাসা করল, “কি হে বাপু? তোমার ধারণা আছে তুমি কত জোরে গাড়ি চালাচ্ছিলে?” হাইজেনবার্গ মাথা দুলিয়ে বললেন, “তা জানি না, কিন্তু এটা জানি আমি এখন কোথায় আছি” 😀
কোয়ান্টাম মেকানিক্স এর অন্যতম প্রবক্তা হাইজেনবার্গ ১৯২৭ সালে যখন তার অনিশ্চয়তা নীতি (Uncertainity principle) লোকসম্মুখে আনেন, তিনি নিজেও কি জানতেন বিশ্ববাসীর কাছে কি অদ্ভুতুড়ে এক ধাঁধা তিনি উপস্থাপন করতে যাচ্ছেন? নীতিটা সোজাসুজি তার ভাষায় এরকম “The more precisely the position is determined, the less precisely the momentum is known.” বাংলা করলে দাঁড়ায়, “যত নির্ভুলভাবে অবস্থান নির্ণয় করা যায়, ভরবেগ জানা হয়ে পড়ে ততটাই অনিশ্চিত”!!
কী হতে পারে বাক্যটার অর্থ?
তোমাদের কাছে এটা আর অজানা নেই – যা কিছু পরিমাপ করা যায় না পদার্থবিজ্ঞানের দৃষ্টিকোণ থেকে তা তাৎপর্যহীন। কোনো জিনিস বিজ্ঞানের আলোচ্য বিষয় হতে হলে প্রথম শর্তই হল তার পরিমাণযোগ্যতা থাকতে হবে। প্রেম ভালবাসার কথা তাই তো ফিজিক্স বইয়ে নয়, কাব্যেই খুঁজে নিতে হয় 😛 এবার একটা ফোটন কণিকার কথা ধর। কোনো বিশেষ মুহূর্তে ফোটন কণিকার অবস্থান ও ভরবেগ নির্ণয়ের উপরেই এর অস্তিত্বের ভৌত তাৎপর্য (physical significance) নির্ভর করে। আমরা জানি, কোনো বস্তুর অবস্থান ও ভরবেগ উভয়েই পরিমাণযোগ্য রাশি। সুতরাং ঐ পিচকি ফোটন আর কে? ওকে পাঠায় দেন আমাদের কাছে, আমরা বের করে দিই ও কই থাকে আর ওর ভরবেগই বা কি!
এই কথা আমরা বলতেই হাইজেনবার্গ দিলেন একখান ভিলেনমার্কা লুক। তিনি ব্যাখ্যা করে দেখালেন, এমন ধারণা ভ্রান্ত। পারমাণবিক পর্যায়ে (Atomic dimension) বা তারও ক্ষুদ্র লেভেলে কোনো বস্তুর অবস্থান ও ভরবেগ একইসাথে নির্ভুলভাবে পরিমাপ করা কোনোক্রমেই সম্ভব নয়। এদের যে কোনো একটি আদর যত্ন দিয়ে সুন্দর করে বের করতে গেলেই অপরটির মান অনিশ্চিত হয়ে পড়বে, পড়তেই হবে!
বললেই হল ইচ্ছামত একটা? এর পিছনে কারণ কী দেখাবেন হাইজেনবার্গ? কারণটা খুব সাদামাটা কথায় এমন – কোনো পরিমাপ বা পর্যবেক্ষণকালে পরীক্ষাধীন বস্তুর কিছু গুণগত পরিবর্তন আমরা ঘটিয়ে ফেলি, যার ফলে বস্তু সম্পর্কে কোনো একটা ধারণা পরিষ্কার হলেও ঐ মুহূর্তে অন্য আরেকটি পরিমাপ (যেটি পরীক্ষণকালে ডিস্টার্বড হয়েছে) সম্পর্কে স্পষ্ট করে জানা যায় না। ফলে চিরকালই আমরা থেকে যায় এক ধাঁধায়, ঘুরপাক খাই হেঁয়ালিতে।
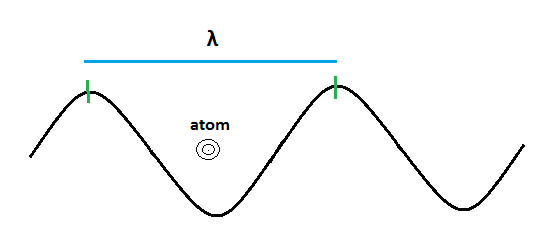
একটা সুন্দর ও কার্যকর উদাহরণ দেখানো যায় এ ব্যাপারে। আমরা জানি দৃশ্যমান আলোর গড়পড়তা তরঙ্গদৈর্ঘ্য 5×10−7 m। অন্যদিকে একটা পরমাণুর ব্যাস হল 10−10 m, একটা প্রোটনের ব্যাস আরো কম 10−15 m, আর ইলেকট্রন? তার ব্যাস হল 10−18 m ক্রমের। তাহলে মজার ব্যাপার কী হল? দৃশ্যমান আলোর তরঙ্গদৈর্ঘ্য ইলেকট্রন-প্রোটন তো বটেই, এমনকি একটা পরমাণুর আকারের চেয়েও হাজারগুণ বড়! অর্থাৎ, একটা পরমাণু নিয়ে তার উপর দৃশ্যমান আলো মারলে কোনো নিশ্চয়তা নেই যে তরঙ্গের সাথে পরমাণুটার মোলাকাত হবে। প্রবল সম্ভাবনা হল, তরঙ্গটা পরমাণুকে না দেখেই তার উপর দিয়ে চলে যাবে।
একটা আস্ত পরমাণুরই যদি এই অবস্থা হয়, তাহলে তুমিই বল – কখনো একটা ইলেকট্রনকে দৃশ্যমান আলোর তরঙ্গ দিয়ে হিট করতে পারবে? ঝামেলার হয়ে যায় না ব্যাপারটা? আচ্ছা? এমন কি কিছু আছে যা ইলেকট্রনের সাথে অব্যর্থভাবে ধাক্কা খেয়ে বলে দিতে পারবে “এই দেখ, এখানে আছে ইলেকট্রন!”
এমন জিনিস সত্যিই আছে এবং তা মোটেও অন্য দুনিয়া থেকে আসা কিছু নয়, 10−18 m তরঙ্গদৈর্ঘ্যের গামা রশ্মি ব্যবহার করেই এই অসাধ্য সাধন করে ফেলা যায় নিশ্চিন্তে 😀 তো ধর তোমার হাতে একটা হাইড্রোজেন পরমাণু আছে, তার বাইরের একমাত্র শেলে বিচরণ করে বেড়াচ্ছে কেবল একটাই ইলেকট্রন। তুমি ঐ ইলেকট্রন কোথায় আছে তা জানতে গামা রশ্মি তাক করলে পরমাণুর উপর এবং রশ্মি ছুঁড়ে মারলে। হ্যাঁ, এবার তুমি ঠিকই ধরতে পারবে কোথায় হিট করল গামা রশ্মি, বলেও দিতে পারবে ঐখানেই ছিল ইলেকট্রনটা। কিন্তু তোমাকে যদি প্রশ্ন করা হয়, ইলেকট্রনের ভরবেগের কী হল? তুমি তখন অপরাধবোধে মাথা নিচু করে ফেলবে 🙁 কারণ তুমি মাত্রই কম্পটন ক্রিয়া ঘটিয়ে ফেলেছ ইলেকট্রনটার সাথে!! সেই ইলেকট্রন এখন আর বসে নেই তার জায়গায়, গতিশক্তি অর্জন করে সে দিয়েছে এক ছুট। অবস্থান জানতে গিয়ে তুমি বেচারা একেবারে ক্লুলেস হয়ে গেলে ঐ সময়কার ভরবেগ সম্পর্কে।
হাইজেনবার্গের মুখে এখন বিজয়ীর হাসি 😀 প্রমাণিত হল – পারমাণবিক পর্যায়ে, কোয়ান্টাম রাজ্যে কোনো কণিকাকে কখনো তুমি ডিস্টার্ব করা ছাড়া কোনো এক্সপেরিমেন্ট করতে পারবে না। একটা এক্সপেরিমেন্ট করে যদি কোনো ফল (অবস্থান) পাও, জানবে না ঐ মুহূর্তে অন্যটি (ভরবেগ) কত। ঠিক এর বিপরীতটাও সত্য – ভরবেগ জানতে গেলে খোঁজ পাবে না কোথায় খেলা করে বেড়াচ্ছে ইলেকট্রন!
এই অবস্থান-ভরবেগ অনিশ্চয়তাকে সমীকরণে রূপ দেওয়া যায়, সেটা তোমরা জানো। সমীকরণটাও জানার কথা (যেটা আমাদের উচ্চ মাধ্যমিকের অনেক লেখকই ভুল উপস্থাপন করেছেন তাদের বইয়ে)। সেটা হল –
সমীকরণটা আমাদের বলছে, অবস্থানের অনিশ্চয়তা ও ভরবেগের অনিশ্চয়তার গুণফল h/4π ধ্রুবকটির সমান অথবা বড়। h হল এখানে প্ল্যাঙ্কের ধ্রুবক। এই সমীকরণে ব্যবহৃত পরিমাপগুলো আমাদের কাছে স্পষ্ট করে উপস্থাপন করা হয় না। সেটা বুঝার জন্য তাহলে একটু সময় ব্যয় করাই যায়!
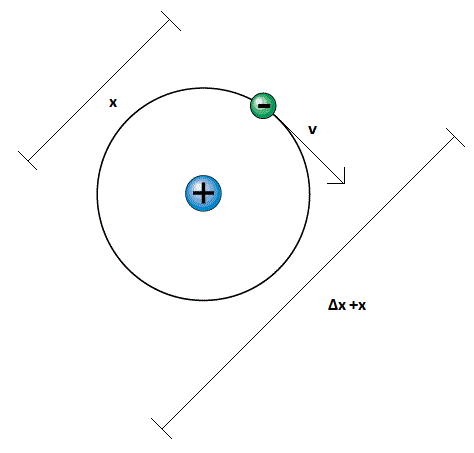
আমরা জানি, বস্তু মাত্রই একটা স্থান দখল করে থাকে। এখন সেই বস্তুটা একটা নির্দিষ্ট অবস্থানজুড়ে থাকলে তার এই নির্দিষ্ট জায়গাটুকুকে আমরা x ধরি। তাহলে Δx কী? Δx হল অবস্থানের অনিশ্চয়তার সূচক। x পরিমাণ ঐ জায়গার বাইরে আরো কতটুকু জায়গাজুড়ে বস্তুটি বিচরণে সক্ষম হতে পারে সেটাই Δx বলে দেয়। উদাহরণ দিই : ধর তুমি তিনটি চেয়ারের একটি লম্বা বেঞ্চে বসে আছ। চেয়ারগুলি প্রত্যেকটি 30cm চওড়া এবং তুমি একটা চেয়ারে আরাম করে বসতে পারো। ঐ বেঞ্চের একটি চেয়ারে গিয়ে বসলে তোমার জন্য x এর মান হবে তাহলে 30cm। কিন্তু ব্যাপারটা তো এমন নয় যে তুমি একটা নির্দিষ্ট চেয়ারেই বসে থাকবে, তুমি চাইলে অন্যদু’টি চেয়ারেও রাজত্ব করতে পারো। তাহলে তোমার নিজের একটি অবস্থান ছাড়াও নড়াচড়া করার ক্ষেত্র এখানে (30+30)cm = 60cm দাঁড়ায়। এই 60cm ই হল Δx এর মান 😀 Δx কে অনেক সময় x এর শতকরা হিসাবে প্রকাশ করা হয়। এই যেমন এখানে Δx হল x এর 200%। অনুরূপভাবে p হল নির্দিষ্ট একটিমাত্র ভরবেগের মান এবং Δp হল ঐ p এর মানের বাইরেও কতটুকু রেঞ্জে ভরবেগ এদিক ওদিক করতে পারে। যেমন 20kgm/s ভরবেগবিশিষ্ট কোনো বস্তুর বেগের বা ভরবেগের অনিশ্চয়তা 10% বললে বুঝতে হবে তা 2kgm/s পরিসরে এদিক ওদিক হতে পারে। মানে তার ভরবেগ সর্বাধিক 1kgm/s কমতে পারে বা 1kgm/s বাড়তে পারে। বাড়া ও কমার এই (1+1)kgm/s = 2kgm/s পরিসরই হল Δp বা ভরবেগের অনিশ্চয়তা।
বোঝাই যাচ্ছে, Δx এর মান বেশি হওয়া মানে কোনো কিছুর অবস্থান সম্পর্কে সঠিকভাবে জানার আশা কমে যাওয়া। কিন্তু যেহুতু Δx ও Δp এর গুণফল ধ্রুবক সুতরাং তাদের মধ্যে ব্যস্তানুপাতিক সম্পর্ক বিদ্যমান। Δx বাড়লে তাই Δp এর মান কমে যাবে, অর্থাৎ কোনো কণিকার অবস্থান নিয়ে যত অনিশ্চিত হয়ে পড়ব আমরা তার ভরবেগ তত সঠিকতার সাথে নিরূপণ করতে পারব। বিপরীতক্রমে বলা যাবে Δp বাড়লে অর্থাৎ ভরবেগ নিয়ে অনিশ্চিত হয়ে পড়লে অবস্থান নির্ণয় নিঁখুত হতে থাকে (যেমনটা ঐ গামা রশ্মির সাথে ধাক্কা খাওয়া ইলেকট্রনের ক্ষেত্রে হয়েছিল 😀 )
অবস্থানের অনিশ্চয়তা কমিয়ে ভরবেগের অনিশ্চয়তাকে বিশাল করে ফেলার উদাহরণ তো আমরা প্রথমেই দেখে ফেলেছি। এবার এসো, Δp এর মান কমালে Δx কীভাবে প্রতিক্রিয়া করে তা দেখে শেষ করি 😀 আবার ফিরে যাই হাইড্রোজেন পরমাণুর কাছে। তোমার এখন খুব ইচ্ছে হচ্ছে ইলেকট্রনের গতিবেগ মাপতে। তুমি নীলস বোরের কাছে গেলে সে তোমাকে বলল হাইড্রোজেনে থাকা ইলেকট্রনটির বেগ নাকি 2.2×106 m/s. তুমি তাকে জিজ্ঞেস করলে, এটা কি সম্পূর্ণ সঠিক হিসাব? বোর বলল, না এর সাথে 10% অনিশ্চয়তা সংশ্লিষ্ট. তাহলে এখানে,
p= mv = (9.11×10−31 ×2.2×106 )kgm/s = 2×10−24 kgm/s
Δp = (10% ×2×10−24 ) = 2×10−25 kgm/s
Δx.Δp = h/4π সমীকরণে Δp এর এই মান বসিয়ে সমাধান করলে Δx এর মান আসে 2.63×10−10 m…
এর অর্থ কী ভাই?
Δx এর অর্থ বোঝার আগে তো জানা লাগবে x কী বোঝায়। হাইড্রোজেন পরমাণুতে x বলতে বোঝায় ইলেকট্রন যে বৃত্তাকার অঞ্চলে ইলেকট্রন মেঘ সৃষ্টি করে থাকতে পারে তার ব্যাস। বোর পরমাণু মডেল আমাদের এই মান 1.06×10−10 m বলে গ্রহণ করতে বলে। অথচ দেখ, এখানে যদি দশ শতাংশ ভরবেগের অনিশ্চয়তা নিয়েও আমরা খুশি থাকি, তাহলে ইলেকট্রন এর অবস্থান সংক্রান্ত অনিশ্চয়তা আসছে 2.63×10−10 m ( অর্থাৎ, 1.06×10−10 m ব্যাসের ঐ বৃত্তাকার মেঘের বাইরেও আরো 2.63×10−10 m পরিমাণ জায়গায় ইলেক্ট্রন বিস্তার লাভ করবে) যা কি না বোরের সুপারিশকৃত ব্যাস 1.06×10−10 m এর দ্বিগুণেরও বেশি!!!
অনিশ্চয়তা কোনো পাঞ্জাবীওয়ালা না হলেও এভাবেই যুগে যুগে আমাদের বুকে জ্বালা ধরিয়ে যাচ্ছে 😛 প্রকৃতি কত যত্ন করেই না রহস্য সাজিয়ে রেখেছে তার পরতে পরতে। এই তো! এখানেই খতম 😀 অনিশ্চয়তা নীতি সংক্রান্ত আরো মজার একটা এক্সপেরিমেন্ট দেখতে ঘুরে আসতে পারো এখান থেকে
শেষ করছি তাহলে আধুনিক পদার্থবিদ্যার আলোচনা। এ যাত্রায় কৃতজ্ঞতার সাথে স্মরণ করছি গুগল, ইউটিউব এবং কোয়ান্টাম ফিজিক্স নিয়ে আলোচনা করা হয়েছে এমন সাইটসমূহকে যা থেকে আমি অবাধে সাহায্য নিতে পেরেছি সিরিজজুড়ে। তবে আমার মতে, আমি সবচেয়ে বড় হেল্প পেয়েছি বাংলা একাডেমি থেকে প্রকাশিত ড. মাসুদ, ড. হামিদ হোসেন ও মুহাম্মদ গোলাম রচিত “পদার্থবিদ্যা” নামের ধ্রুপদী বইটি থেকে। বাংলা ভাষায় পদার্থবিজ্ঞানকে বিকশিত করার নেপথ্যে থাকা এই মহান লেখকদের জানাই বিনম্র শ্রদ্ধা।

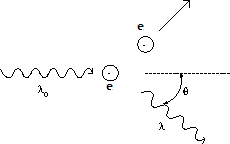
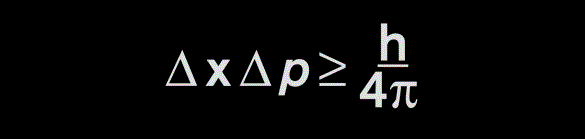
খুব বেশি অসাধারণ একটা লেখা 🙂
ধন্যবাদ 🙂
ড. মাসুদ, ড. হামিদ হোসেন ও মুহাম্মদ গোলাম রচিত “পদার্থবিদ্যা” বইটার পিডিএফ পাওয়া যাবে ?
এত পুরনো বইয়ের পিডিএফ পাওয়া যাবে না তা সম্পর্কে আমি সন্দিহান। আমার নিজের কাছেও হার্ড কপি আছে, আমি তা কিনতেই সাজেস্ট করব। খুব বেশি কিছু না, বাংলা একাডেমির বই বিক্রয় কেন্দ্রে গেলেই এই বইটা পাওয়া যাবে।
খুবই সুন্দর। আমি ভারতীয়। আমি বাংলা একাডেমি থেকে প্রকাশিত ড. মাসুদ, ড. হামিদ হোসেন ও মুহাম্মদ গোলাম রচিত “পদার্থবিদ্যা” নামের বইটি ডাকযোগে কিনতে চাই। এ ব্যাপারে কিছু সাহায্য করতে পারেন কি?
বাংলা একাডেমীর পুস্তক বিক্রয় ও বিপণন শাখা বরাবর চিঠি লিখে বইটা পেতে পারো। এটার মোট তিনটা খন্ড আছে। তিনটি খন্ডের মোট দাম ৪০০ টাকার মত।
This books(3 parts) r sold out & they won’t republished those
কত শতাংশ অনিশ্চয়তা যুক্ত আছে সেটা হিসেব করার সময় ইলেকট্রনের নিশ্চল ভর দিয়ে ভরবেগ হিসেব না করে আপেক্ষিক ভর দিয়ে ভরবেগ হিসেব করার প্রয়োজন আছে কিনা ?
ইলেক্ট্রনের যে বেগ ধরে এখানে হিসাব-নিকাশ করা হয়েছে তা আলোর বেগের 136 গুন কম। আপেক্ষিকতার জন্য গুরুত্ববহ হতে এটা অনেকটাই কম বেগ বলে এখানে আপেক্ষিক ভর হিসাবের দরকার পড়ে নি।
আরেকটি অপ্রাসঙ্গিক প্রশ্ন করছি কৌতূহল থেকে , যেহেতু ভর এবং শক্তির রূপান্তর সম্ভব এবং শক্তির একক ফোটন তাহলে কি বিশ্বের সমস্ত ভর বা পদার্থ কি ফোটন দ্বারা তৈরী ? যদি তা না হয় অর্থাৎ ফোটন যদি শুধু শক্তির একক ই হয় তাহলে ভরের একক কি ?
কোয়ান্টাম ফিজিক্সের যত গভীরে যাওয়া যায়, ভর নামের রাশিটা ততই মূল্যহীন হতে থাকে। পরমাণুর পিছনে লাগা মানুষ তার অভ্যন্তরে সুন্দর করে সাজানো ইলেক্ট্রন – প্রোটন দেখে না, টর্নেডোর মত বিস্তৃত শক্তি তরঙ্গই (Energy wave) দেখে। আধুনিক পদার্থবিজ্ঞান আমাদের এটাই শেখায় যে আমরা প্রকৃপক্ষ বস্তু না, শক্তি দিয়েই তৈরি। ভরের ধারণাকে প্রাধান্য দিয়ে গড়ে উঠেছিল সনাতনী বা নিউটনীয় পদার্থবিদ্যা, তাই সেভাবে এসেছিল ভরের এককও। আমরা সনাতনী পদার্থবিদ্যা ফেলে দিই নি কারণ দৈনন্দিন জীবনে আমরা কাজে লাগাই এটাকেই। তাই ভর থাকছে, থাকবে। যদিও ভর আসলে শক্তির একপ্রকার রূপ ছাড়া অন্য কিছুই নয় – যা মডার্ন ফিজিক্স আমাদের জানায় (আবার প্রথম কথাতেই ফিরে গেলাম)।
ভাইয়া তুমি কোন universityte poro???