১৯২৩ সালে এক্স রে এর বিক্ষেপণ (X-ray scattering) পর্যবেক্ষণকালে বিজ্ঞানী কম্পটন লক্ষ্য করেন এক্স রে যদি কোনো মুক্ত ইলেকট্রনের সাথে সংঘর্ষে লিপ্ত হয় তবে এক্স রশ্মি তার দিক পরিবর্তন করে এবং ফলশ্রুতিতে তার কম্পাংক হ্রাস পায়! এক্স রশ্মি ব্যবহার করে প্রাপ্ত এই ঘটনাকে বিজ্ঞানীর নামানুসারে আমরা কম্পটন প্রভাব (Compton effect) বলেই জানি। উচ্চ মাধ্যমিক সিলেবাসের নবতর সংযোজনের একটি হল এই কম্পটন ইফেক্ট; এই সম্পর্কে প্রত্যেকের পরিষ্কার ধারণা রাখা এখন তাই সময়ের দাবীই বটে 😛
কম্পটন প্রভাবে আসলে কী ঘটে কেন ঘটে তা বোঝার জন্য চল আমরা একে একটু ক্লোজ ভিউ থেকে দেখি। ধর তোমার কাছে একটা এক্স রে টিউব আছে যা থেকে তুমি এক্স রশ্মি নির্গত করতে পারবে। এখন এই এক্স রশ্মিকে কী করব? তাকে ফেলব আমাদের একটা টার্গেটের উপর। টার্গেট যে সে হলে কিন্তু হবে না, হতে হবে এমন কিছু যাতে মুক্ত (বন্ধনে অংশ নেয় নি এমন) ইলেকট্রন আছে। গ্রাফাইট এক্ষেত্রে তাই বেশ ভালই মানিয়ে যায় আমাদের টার্গেট হিসেবে। এই টার্গেটে এক্স রশ্মি ফেললে দেখা যাবে এক্স রশ্মি বিক্ষিপ্ত হচ্ছে নানা দিকে।
বিক্ষেপণ তো ঘটছে, এখন কী করব? কিছুই না! তরঙ্গদৈর্ঘ্য মাপার একটা যন্ত্র স্পেক্ট্রোগ্রাফ তোমার হাতে নাও ও টার্গেটের চারপাশে তাকে ঘুরিয়ে ঘুরিয়ে বিভিন্ন কৌণিক অবস্থানে এক্স রশ্মির তরঙ্গদৈর্ঘ্য মাপতে দাও। যেমন এই ছবিটাতে দেখ, এক্স রশ্মি তার আগত দিক থেকে φ কোণে ঘুরে গেছে। এই বরবার এক্স রশ্মি তোমার ডিটেক্টরে এসে পড়লে সে রিডিং দেবে কত তরঙ্গদৈর্ঘ্যের এক্স রে সে সবচেয়ে পাচ্ছে। তবে মূল কথা হল, তুমি বিভিন্ন অবস্থানে যে বিভিন্ন তরঙ্গদৈর্ঘ্য পাবে এই সকল মানই কিন্তু তুমি যে এক্স রশ্মি একেবারে প্রথমে ফেলেছিলে, তার তরঙ্গদৈর্ঘ্যের চাইতে কম হবে। এই আলাদা দু’টি তরঙ্গদৈর্ঘ্য উল্লেখ করার জন্যই দেখ ছবিতে আগত এক্স রে কে লাল ও বিক্ষিপ্ত এক্স রে কে নীল রঙে চিহ্নিত করা হয়েছে।
কম্পটন এরপর একটা বুদ্ধিমানের মত কাজ করলেন। তিনি করলেন কি, বিভিন্ন কৌণিক অবস্থানের জন্য যে তরঙ্গদৈর্ঘ্যে এক্স রশ্মি সবচেয়ে বেশি পাওয়া যাচ্ছে সেটা নিয়ে একটা গ্রাফ আঁকলেন। তিনি মোট চারটা কৌণিক অবস্থান নির্বাচন করলেন – 0°, 45°, 90° এবং 135°। এর মধ্যে 0° বলতে বোঝানো হচ্ছে – বিক্ষেপণ না করেই তিনি স্পেক্ট্রোগ্রাফ ব্যবহার করে এক্স রশ্মির তরঙ্গদৈর্ঘ্য মাপলেন। এই এক্স রশ্মির তরঙ্গদৈর্ঘ্য তো তাহলে আপতিত এক্স রে এর তরঙ্গদৈর্ঘ্যই নির্দেশ করে, তাই না? 😀
গ্রাফটা দেখ নিচের মত হয়, খুব সাবধানে খেয়াল করে কিন্তু!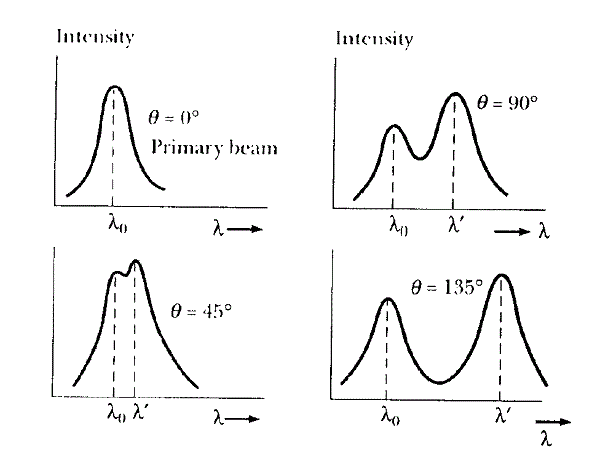 এখানে কী হচ্ছে আবার একটু ভেঙ্গে বলি। উপরের বামের ছবিটা দেখ। এই গ্রাফ পাওয়া যাচ্ছে আপতিত এক্স রশ্মির জন্য, আমরা এখানে x অক্ষে আপতিত এক্স রে এর তরঙ্গদৈর্ঘ্য নিচ্ছি এবং y অক্ষে বিবেচনা করছি ঐ তরঙ্গদৈর্ঘ্যের জন্য কতটুকু তীব্রতা পাওয়া যাচ্ছে। কোনো তরঙ্গদৈর্ঘ্যের জন্য তীব্রতা পাবার অর্থ হল, ঐ নির্দিষ্ট তরঙ্গদৈর্ঘ্য কত বেশি পরিমাণে আপতিত এক্স রে এর মধ্যে উপস্থিত আছে। অর্থাৎ এটা বুঝে গেছ, যেসব এক্স রশ্মি এসে পড়বে তাদের সবার তরঙ্গদৈর্ঘ্য এক হবে এমন কোনো কথা নেই। যে তরঙ্গদৈর্ঘ্যের রশ্মি তুলনামূলক বেশি থাকবে বা যার জন্য তীব্রতা বেশি হবে তাকেই আমরা আপতিত এক্স রে এর তরঙ্গদৈর্ঘ্য বলে জানব। এই তরঙ্গদৈর্ঘ্যকে প্রকাশ করা হচ্ছে দেখ λ0 প্রতীক দ্বারা। বিক্ষেপণ না হলে কেবল এই তরঙ্গদৈর্ঘ্যের এক্স রশ্মির জন্যই সর্বোচ্চ পরিমাণ তীব্রতা পাওয়া যাবে।
এখানে কী হচ্ছে আবার একটু ভেঙ্গে বলি। উপরের বামের ছবিটা দেখ। এই গ্রাফ পাওয়া যাচ্ছে আপতিত এক্স রশ্মির জন্য, আমরা এখানে x অক্ষে আপতিত এক্স রে এর তরঙ্গদৈর্ঘ্য নিচ্ছি এবং y অক্ষে বিবেচনা করছি ঐ তরঙ্গদৈর্ঘ্যের জন্য কতটুকু তীব্রতা পাওয়া যাচ্ছে। কোনো তরঙ্গদৈর্ঘ্যের জন্য তীব্রতা পাবার অর্থ হল, ঐ নির্দিষ্ট তরঙ্গদৈর্ঘ্য কত বেশি পরিমাণে আপতিত এক্স রে এর মধ্যে উপস্থিত আছে। অর্থাৎ এটা বুঝে গেছ, যেসব এক্স রশ্মি এসে পড়বে তাদের সবার তরঙ্গদৈর্ঘ্য এক হবে এমন কোনো কথা নেই। যে তরঙ্গদৈর্ঘ্যের রশ্মি তুলনামূলক বেশি থাকবে বা যার জন্য তীব্রতা বেশি হবে তাকেই আমরা আপতিত এক্স রে এর তরঙ্গদৈর্ঘ্য বলে জানব। এই তরঙ্গদৈর্ঘ্যকে প্রকাশ করা হচ্ছে দেখ λ0 প্রতীক দ্বারা। বিক্ষেপণ না হলে কেবল এই তরঙ্গদৈর্ঘ্যের এক্স রশ্মির জন্যই সর্বোচ্চ পরিমাণ তীব্রতা পাওয়া যাবে।
কিন্তু ঠিক তার নিচের চিত্রে কাহিনী ভিন্ন। এখানে আমরা 45° কোণে বিক্ষিপ্ত তরঙ্গদৈর্ঘ্যগুলো মাপতে গিয়ে দেখলাম এতে λ0 তরঙ্গদৈর্ঘ্যবিশিষ্ট এক্স রশ্মির পরিমাণ তুলনামূলক কম, বরং আরেকটা নতুন তরঙ্গদৈর্ঘ্যের জন্য বেশি তীব্রতা পাওয়া যাচ্ছে। এই নতুন তরঙ্গদৈর্ঘ্য দেখ λ0 এর চেয়ে বেশি (x অক্ষের ডানে সরে গেছে)। 90° এর জন্য এই পরিবর্তীত নতুন তরঙ্গদৈর্ঘ্যের জন্য তীব্রতা আরো বেশি পাওয়া যায় ও এই তরঙ্গদৈর্ঘ্য আরো বেড়ে যায়, 135° এর জন্য একই ঘটনা আরো চূড়ান্ত লেভেলে ঘটে। এতকিছু বিশ্লেষণ করে আমরা কী সিদ্ধান্ত নিতে পারি?
সিদ্ধান্ত নিতে পারি এটা যে λ’-λ0 এর পার্থক্য ততই বাড়ে বিক্ষেপণ কোণের মান যত বেশি হয় 😀 এটুকু ধরতে পারলেই অনেকটুকু বুঝে গেছি আমরা 😛
এখন কথা আসবে কার্যকারণ নিয়ে। সবচেয়ে বেসিক পার্ট এটাই, কী এমন হয় এক্স রে এর যে ইলেকট্রনের সাথে ধাক্কা খেয়ে তার তরঙ্গদৈর্ঘ্যও কমে যায়? যদি আপতিত এক্স রে কে আমরা তড়িৎচৌম্বক তরঙ্গ বলে কল্পনা করি তবে বিক্ষিপ্ত এক্স রশ্মিতে λ’ তরঙ্গের উপস্থিতি ব্যাখ্যা করা সম্ভব হয় না। কেন? কারণ তড়িৎচৌম্বক তরঙ্গ এর স্বীকার্য অনুযায়ী এক্স রশ্মি যদি λ0 তরঙ্গদৈর্ঘ্য নিয়ে আসে তবে তার বিক্ষেপ ঘটার পরেও একই তরঙ্গদৈর্ঘ্য বজায় থাকা উচিত। অথচ, আমরা দেখি বিক্ষেপের ফলে এই λ0 এর উল্লেখযোগ্য পরিবর্তন হয়! কি মুশকিল! 🙁 তাহলে কীভাবে ব্যাখ্যা করব এটাকে?
কম্পটন তখন আশ্রয় নিলেন কোয়ান্টাম তত্ত্বের। তিনি প্রস্তাব করলেন, এক্স রে তরঙ্গের আকারে নয় বরং ফোটনের আকারে ইলেকট্রনের সাথে সংঘর্ষে লিপ্ত হয় ও বিক্ষিপ্ত হয়। এই ফোটনের ধারণকৃত শক্তি যদি hƒ0 হয় তবে তার এই শক্তির একাংশ আঘাতপ্রাপ্ত ইলেকট্রনের গতিশক্তির যোগান দেয় এবং বাকী শক্তিটুকু নিয়ে ফোটনটি বিক্ষিপ্ত হয়। সুতরাং লেখা যায় hƒ0 = hf + 1/2 mv2. এই hf ই হল নতুন কম্পাংবিশিষ্ট ফোটনের শক্তি। যেহেতু শক্তি কমার কারণে এখানে কম্পাংক কমে যায় ফোটনের সুতরাং বিক্ষেপের পর তরঙ্গদৈর্ঘ্য না বেড়ে কি আর পারবে? 😀
কোয়ান্টাম তত্ত্ব দিয়েই যে আসলে এটার ব্যাখ্যা হয় তার ক্লু কিন্তু আগেই দেওয়া ছিল কোথাও 😛 বল তো কোথায়? (একটা ছবিতেই উত্তর পাবে)
উপরে যে সমীকরণটা লিখেছিলাম, এটা থেকে আরও দেড় দুই পৃষ্ঠা বিদঘুটে প্রতিপাদনের পর আমরা কম্পটন ইফেক্ট সংক্রান্ত সবচেয়ে কাজের সমীকরণটা পাই। সেটা হচ্ছে
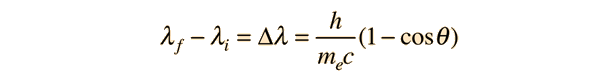
ওমা! এখানে আবার এসব কী কী এল? এখানে যেসব রাশি আছে তাদের সাথে পরিচয় করিয়ে দিচ্ছি, এখানে λ’-λ0 কেই Δλ বলা হচ্ছে। অর্থাৎ এটা হচ্ছে এক্স রে বিক্ষেপণের পর কতটুকু তরঙ্গদৈর্ঘ্য বাড়ল সেই হিসাবটা। ডানপক্ষে তাকিয়ে দেখ, সব্বাই ধ্রুবক কেবল একজন ছাড়া। এখানে h প্ল্যাঙ্কের ধ্রুবক, নিচের m হল ইলেকট্রনের ভর আর c হল আলোর বেগ। এখানে θ ই কেবলমাত্র চলক কেননা তার বিভিন্ন মানের জন্যই আমরা Δλ বিভিন্ন বিভিন্ন পাই।
h/mc চেহারার যে জিনিসটা দেখতে পাচ্ছ এটা কিন্তু খুব ভাল একটা কাজের জিনিস। এটাকে বিজ্ঞানীরা আদর করে ডাকেন কম্পটন ভ্রংশ (Compton shift) নামে। কম্পটন শিফটের মান যে নির্দিষ্ট কিছু হবে এটা তো বোঝাই যায়। ইলেকট্রনের সাথে সংঘর্ষের দরুণ জন্য আমরা যদি কম্পটন ভ্রংশ এর মান বের করি তবে তা আসবে 2.43×10−12 m। ইলেকট্রনের সাথে সংঘর্ষে এক্স রশ্মি দিক পরিবর্তন করে বলে এখানে জড়িত ইলেকট্রনকে প্রতিক্ষেপ (Recoil) ইলেকট্রন নামেও ডাকা হয়। এই প্রতিক্ষেপ ইলেকট্রন কিন্তু ফোটন থেকে গতিশক্তি লাভ করে যা আগেই উল্লেখ করেছি (একেবারে প্রথম ছবিতেও ইলেকট্রনের ছুটে যাওয়া দেখতে পাবে)। উইলসন, বোথে এবং বেকার নামের তিনজন বিজ্ঞানী সর্বপ্রথম কম্পটন প্রভাবের কারণে প্রতিক্ষেপ ইলেকট্রনের সন্ধান লাভ করেন।
শেষের কথা, কিন্তু সবচেয়ে মজার কথা। ইলেকট্রনের জন্য কম্পটন ইফেক্ট এতক্ষণে আলোচনা করলাম বলে কম্পটন ভ্রংশ নির্ণয় করতেও ইলেকট্রনের ভর ব্যবহার করেছি। যদি এক্স রশ্মি ইলেকট্রনের সাথে সংঘর্ষে না লিপ্ত হয়ে একটা প্রোটনের সাথে লিপ্ত হয় তখন?
তখন আর কী? সবকিছু ঠিক থাকবে, কেবল কম্পটন ভ্রংশ বের করতে m এর জায়গায় প্রোটনের ভর বসিয়ে দিলেই কেল্লা ফতে 😀 তাহলে বল তো, ইলেকট্রনের সাথে না ধাক্কা খেয়ে প্রোটনের সাথে সংঘর্ষ ঘটলে Δλ এর মানের কেমন পরিবর্তন ঘটবে?
ভাল কথা, কম্পটন কিন্তু তার কাজের জন্য বছর চারেক পর ১৯২৭ সালেই নোবেল পুরস্কার পেয়ে গিয়েছিলেন! 😀
আগের পর্ব : আধুনিক পদার্থবিদ্যা ২ : বিগবস ব্রগলি
পরবর্তী পর্ব : আধুনিক পদার্থবিদ্যা ৪ : হাইজেনবার্গের অনিশ্চয়তা নীতি

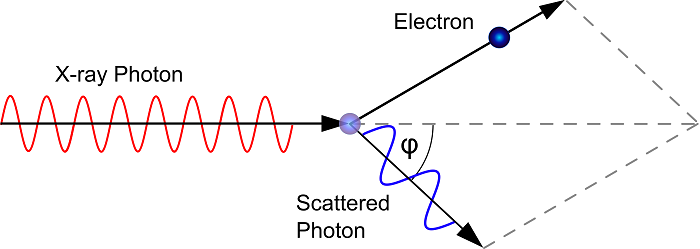
তারমানে কি শুধু সংঘর্ষের সময় এক্স রে কণার মত আচরণ করছে ? আর বাকি সময় তাড়িতচৌম্বক তরঙ্গ ?
সংঘর্ষের বিষয়টি ব্যাখ্যা করতে এখানে আলোর কোয়ান্টাম তত্ত্ব প্রয়োজন হচ্ছে, অন্যান্য অনেক আলোকীয় ঘটনা তড়িৎচৌম্বক তরঙ্গ দিয়ে ব্যাখ্যা সুবিধাজনক। বিজ্ঞানীদের যখন যেটা সুবিধা সেটা দিয়ে আলোকীয় ঘটনাগুলো ব্যাখ্যার চেষ্টা করেছেন। কারণ আলোকে বাঁধাধরাভাবে তরঙ্গ বা কণা হিসেবে আখ্যাদান সম্ভব নয়।
আলো তড়িৎ ক্রিয়া এবং কম্পটন ক্রিয়ার মধ্যে পার্থক্য কি