ফাংশন:
ফাংশন(Function) এবং অন্বয়(Relation)-শব্দ দু’টো এক সাথেই আমাদের শুনতে হয় বেশিরভাগ সময়ে! এবং মজার ব্যাপার হচ্ছে,আমরা সবচেয়ে বেশি কনফিউজড হয়ে যাই এই ব্যাপারটা নিয়েই!
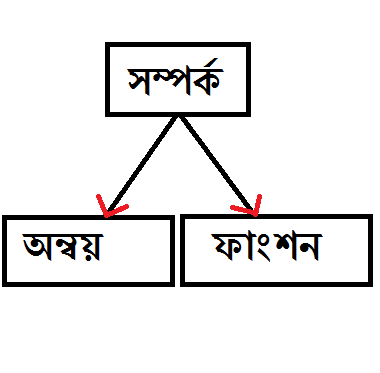
Set Theory পড়ার সময়ে অনেকেই ”অন্বয়” শব্দটার ব্যাপারে শুনে থাকে। মূলত: দু’টি সেটের সদস্যদের মধ্যে ”সম্পর্ক” নির্ণয়ের স্বার্থেই এই ”অন্বয়” এবং ”ফাংশন” ব্যাপারটি আসে। একটি ছক দেখে আসি।
আমরা দু’টো সেট নিয়ে নিই ঝটপট! আলোচনা কোনদিকে যাবে তোমরা নিজেরাই বুঝে যাবে।
ধরি,
A = { 2 , 3 , 4 }
B = { 5 , 6 , 7 }
এবার আমি এই দুই সেটের মধ্যে একটি সম্পর্ক লিখবো,এবং সেটাকে আমরা ”ফাংশন” বা ”অন্বয়” একটা নাম দিয়ে দিবো!
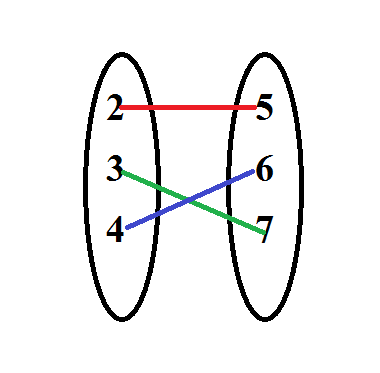
ধরা যাক,সেট দু’টির মাঝে প্রথম সম্পর্কটা এমনঃ
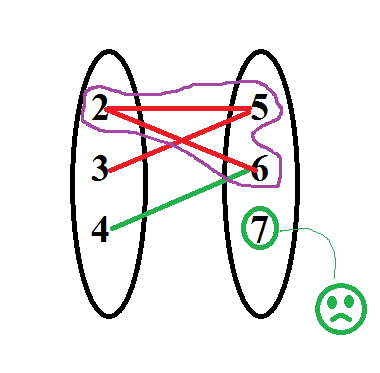
এইটা ফাংশন! কারণ কি? কারণ হচ্ছে আমরা ধরে নিয়েছি বাম পাশের সেটটি {২,৩,৪} ডানপাশের সাথে সম্পর্কযুক্ত। এখানে,বাম পাশের প্রতিটা উপাদানের জন্য ডানপাশের সেটটার একটামাত্র ( দুইটা হলেও হবেনা,একটাই হতে হবে! ) উপাদান যদি থাকে,তাহলে সেটা ফাংশন!! বিভিন্ন আউটপুটের পিছনে যদি সেইম টাইপের ইনপুট জড়িয়ে থাকে,তবে সেটা ফাংশন হবেনা,সেটা হবে ”অন্বয়”। অনেকটা এরকম, বানাতে চাচ্ছো আপেলের জুস,আপেল ও দিলা,কিন্তু একবার হলো কমলার জুস আবার আরেকবার হলো আপেল জুস! মানে মেশিনের মাথা নষ্ট হয়ে আছে ধরা যায়। এই ভদ্রলোক ফাংশন নয়। ব্যাপারটা এমনঃ
৭ দুঃখ পাচ্ছে কারণ তার সাথে কেউ সম্পর্কে যাচ্ছেনা। ও যা খুশি হউক! আচ্ছা,উপরের এই উদাহরণটাই হচ্ছে অন্বয়-এর,এটা কিন্তু ফাংশন না! কারণ কি? কারণ হচ্ছে ইনপুট যখন ২ , তখন আউটপুট ৫ ও হচ্ছে আবার ৬ ও হচ্ছে! এইটা ফাংশনের নিয়মের বাইরের কথা,তাই এটি ”অন্বয়”। সেট দুইটিকে আমরা অন্বয় এর সাহায্যে প্রকাশ করতে পারি এভাবেঃ
S : A —> B
কোন সম্পর্কটি ফাংশন আর কোনটি অন্বয়,তা আমরা Vertical Line Test এর মাধ্যমে গ্রাফ থেকে খুব সহজেই বলে দিতে পারি! আমরা কয়েকটি সম্পর্ক ধরে নিই,যাচাই করবো কে কে ফাংশন আর কে কে ফাংশন না।
ধরে নিলামঃ
এবার আমরা সম্পর্কগুলোর গ্রাফ এঁকে ফেলিঃ
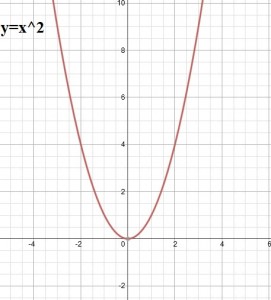
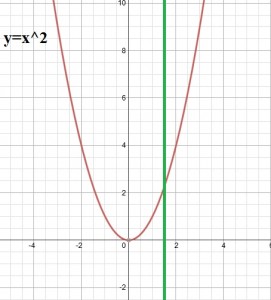
F(x) = x^2 এর জন্য গ্রাফটি হবেঃ
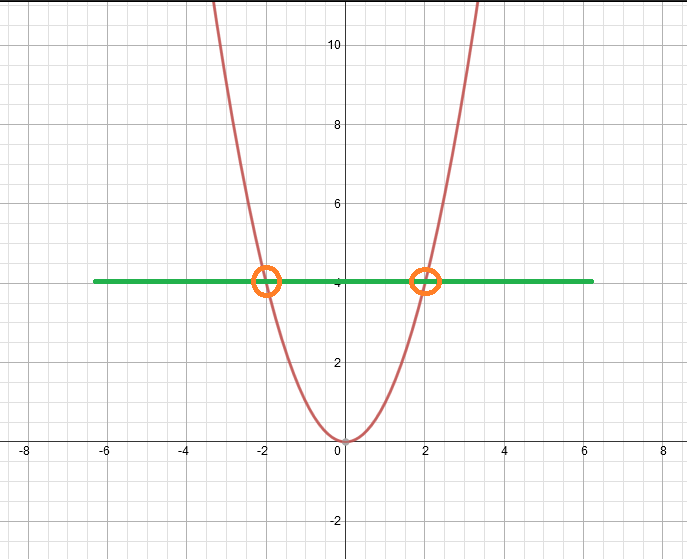
এটি ফাংশন কি ফাংশন না,তা আলোচনা করা যাক! খেয়াল করি,আমরা যদি y-অক্ষের সমান্তরালে ( মানে,x-অক্ষের উপর লম্বভাবে ) একটি সোজা দাগ টানি,তাহলে তা একটি বিন্দুর বেশি বিন্দুতে গ্রাফটিকে ছেদ করেনা। চিত্রে দেখিঃ
ঐ যে দেখো ১ দশমিক ৫ এর একটু পরের ভুজটিতে সবুজ রেখাটি ছেদ করেছে,আর কোথাও করেনি। তাই এটি একটি ফাংশন। যদি একের অধিক বিন্দুতে ছেদ করতো,তাহলে এটি আর ফাংশন হতোনা! দ্বিতীয় উদাহরণটি দেখা যাকঃ
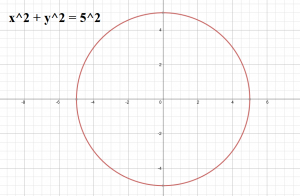
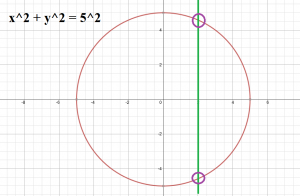
এবার আগের মতো আবার Vertical Line টেনে ফেলিঃ
খেয়াল করে দেখলে!! সবুজ লাইনটি কিন্তু দু’টো পয়েন্টে ছেদ করে ফেলেছে! তাই এটি আর ফাংশন হবেনা,বৃত্তের সমীকরণটি তাহলে ফাংশন নয়!! এটি কেবল একটি অন্বয়,যাকে আমরা সমীকরণের মাধ্যমে প্রকাশ করি। আসলে,ইন্টারে যারা পড়ছো,তারা কনিক্স পড়েছো নিশ্চয়ই!! কনিক্স এর কেউই ফাংশন নয়,সবাই অন্বয়,এবং সবাই স্রেফ x এবং y এর মধ্যে একটি সম্পর্ককে ইকুয়েশনের মাধ্যমে তুলে ধরে,আর কিছু না। নিজেরা ছবিগুলো এঁকে দেখবে কনিক্সের। আর Vertical Line টেস্টটাও করবে!
( এই Vertical Line Test কেন কাজ করে,তা নিয়ে একটু ভেবে দেখো,খুবই সহজ একটি ঘটনা। তোমাদের চিন্তার খোড়াক হিসেবে দিয়ে দিলাম। কেউ পারলে কমেন্ট বক্সে সেটা জানাতে ভুল করো না! )
‘’ফাংশন’’ নামক গণিতের এই গুরুত্বপূর্ণ একটি শাখার মূলতঃ উদ্ভব হয় সপ্তবিংশ শতাব্দীর দিকে, বিশ্লেষণধর্মী জ্যামিতি এবং ক্যালকুলাস ( আবিষ্কারক : লিবনিজ/পীথাগোরাস ) শাখাগুলোর উন্নতিকরণের মধ্য দিয়েই। যদিও এই শাখাটির ধারণা গণিতবিদেরা প্রাচীনকালেই লাভ করে! তবে আমরা শুরুর দিকে Dieudonné এবং Ponte – এর ধারণা দিয়েই শুরু করলাম। 😀
আমি আমার প্রথম লিখাতেই বলছিলাম,ফাংশন ধারণাটা আসলে একটি মেশিন বৈকি কিছু না। এটি কিছু সংখ্যা,কিছু অপারেটর,কিছু গাণিতিক হিসাবের উপাদানকে গ্রহণ করে,তারপর তাকে নিজের কর্মচরিত্র অনুযায়ী মোডিফাই করে আউটপুট দিয়ে দেয়। ফাংশন অনেক রকম আছে! সবগুলোর প্রকারভেদ সম্পর্কে এখানে লিখতে গেলে এমন হতে পারে ওয়েবসাইটের হোস্টিং শেষ হয়ে গিয়েছে,কিন্তু আমার লিখা শেষ হয়নি। তাই একটি লিংক দিচ্ছি,যাদের জানার প্রয়োজন সেখান থেকেই জেনে নিতে পারবেঃ
http://functions.wolfram.com/
ফাংশন কি?
” ইনপুট নিবে,আউটপুট দিবে- এই মর্মে বিশ্বাসী এক মেশিন! ”
উদাহরণ দিলে একটু ভালো হয় :
সহজ একটি ব্যাপার!! ধরা যাক, একটি ফাংশন ( মেশিন ) এর কাজ হচ্ছে সে যেই সংখ্যাটাকে পাবে,তাকে ধরেই চারগুণ করে দিবে! এই মেশিনটার নাম আমরা দিতে পারি:
f(x) = 4x
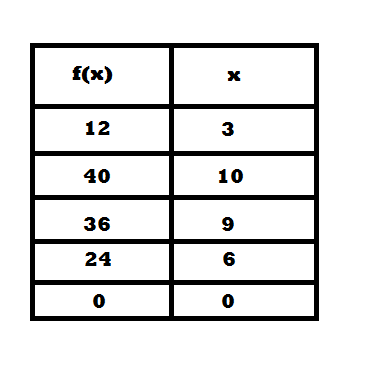
এখন এখানে কিছু নাম্বার ইনপুট দিয়ে দিই!
দেখতেই পাচ্ছো,ইনপুট হিসেবে x কে নিয়ে তাকে চারগুণ করে y=f(x) ফাংশনটি আউটপুট দিয়ে দিচ্ছে। শুণ্য কে চারগুণ করলে শুণ্য ই হয়,তাই তার আউটপুটে পরিবর্তন আসে নি।
তো মোটামুটি ফাংশনের নামকরণের ধারণা এতটুকুই যথেষ্ট। মানে,কেন এর নাম ফাংশন,কি কাজ এটার,এগুলো। এখন ধীরে ধীরে এর কিছু বৈশিষ্ট্য সম্পর্কে জানতে জানতে ভিতরে আগানোর চেষ্টা করবো। J
এক–এক ফাংশনঃ
এটি কি? এটি একধরণের ফাংশন।
কেমন হয় এটি দেখতে? আমরা উপরের আলোচনায় y=x^2 কে ফাংশন বলে এসেছি,মনে আছে? সেই ফাংশনটি কিন্তু এক-এক নয়!
কেন নয়? সেটি বললেই তোমাদের কাছে এক-এক ফাংশনের ব্যাপারটি একেবারে পরিষ্কার হয়ে যাবে।
দেখো,y=x^2 ফাংশনটিতে আমরা যখন ইনপুট হিসেবে -2 দিচ্ছি,আমরা আউটপুট পাচ্ছি 4(চার)। ঠিক তেমনিভাবে আমরা যখন ইনপুট দিয়ে দিচ্ছি +2,তখনো আমরা সেইম আউটপুটটাই পাচ্ছি,4 ( চার) !! এটা ফাংশনের রীতিকে ভেঙ্গে ফেলছেনা সত্য,কিন্তু এটি একটি বিশেষ মর্যাদা নষ্ট করে ফেলছে। তাই এটিকে আমরা এক-এক ফাংশন বলতে পারবো না।
তাহলে এক-এক ফাংশন কারা? যেসব ফাংশনে প্রতিটি স্বতন্ত্র ইনপুটের জন্য একটি স্বতন্ত্র আউটপুট থাকবে। যেমন ধরো, y = x^3 । তুমি ইনপুট হিসেবে যা-ই দাও না কেন,আউটপুট সবসময় ব্যতিক্রমধর্মীই পাবে! বই খাতায় আমরা এটা যেভাবে করতামঃ
ধরি,
f(x) = x^2
ধরা যাক, x1,x2 are element of F
তাহলে,
F(x1) = F(x2)
- x1^2 = x2^2
- x1 = (+/-) x2
দেখাই যাচ্ছে,এখানে ভিন্নভিন্ন টাইপের ইনপুট ( x1 আর x2 সেইম হলেও , x1 আর –x2 কিন্তু সেইম নয়,তাদের চিহ্নে পরিবর্তন রয়েছে ) থাকা সত্ত্বেও আউটপুট একই আসছে। মানে,F(x1) এবং F(x2) , এই দু’টো আউটপুটই আসছে,রাইট? প্রথম লাইন দেখো,এরা সমান। তাই F(x) = x^2 ফাংশনটি এক-এক নয়।
একইভাবে, y=x^3 ফাংশনটি ”কেন” এক-এক তাও প্রমাণ করে ফেলো! 😀
( Note : একটি ফাংশন এক-এক কিনা , তা চেক করার জন্য Horizontal Line Test রয়েছে,যা হুবুহু Vertical Line Test এর মতোই! শুধু দাগটা টানতে হয় ”x-অক্ষের সমান্তরালে”। যদি রেখাটি গ্রাফটিকে একের অধিক বিন্দুতে ছেদ করে,তাহলে সেটি এক-এক ফাংশন নয়। নিজেরা চেষ্টা করো তো!! আলসেমী লাগে? -_- আচ্ছা আমিই করে দিচ্ছি! তাও শিখে রাখো! )
পরিস্কার?
সার্বিক ফাংশনঃ
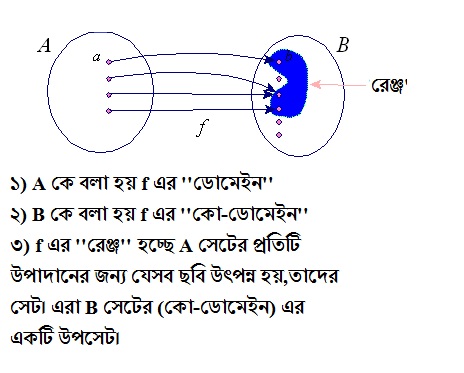
যখন একটি ফাংশনের কোডোমেন এবং রেঞ্জ সেট দু’টি একই হয়,তখন আমরা সেই ফাংশনকে সার্বিক ( অনটু ) ফাংশন বলে থাকি। ডোমেইন হচ্ছে ইনপুটের সেট,আর কোডোমেইন হচ্ছে ”সম্ভাব্য” আউটপুটের সেট। রেঞ্জ সবসময়ই কো-ডোমেনের অন্তর্গত একটি সেট হয়ে থাকে। আমরা ধরে নিই,সবগুলো ইনপুটের জন্য যেসকল আউটপুট হতে পারে,তারা একটি সেটের মধ্যে রয়েছে। এবার আমাদের ধরে নেয়াটি যদি একেবারেই ১০০% সঠিক হয়,মানে বলতে চাচ্ছি যতগুলো উপাদানকে ধরে নিয়েছি সম্ভাব্য আউটপুট হিসেবে,তাদের সবাইই যদি আউটপুট হিসেবে মনোনীত হয়,তাহলে সেই ক্ষেত্রেই আমরা বলতে পারি যেঃ
কো-ডোমেইন ( সম্ভাব্য আউটপুট ) = রেঞ্জ ( আউটপুট )
এবং তখনি ফাংশনটি সার্বিক হয়।
আমরা ফাংশনের নোটেশন হিসেবে একটি পদ্ধতি ব্যবহার করি,যেটি অনেকটাই এরকমঃ
f :A —> B
এখানে A হচ্ছে ডোমেইন,আর B হচ্ছে কো-ডোমেইন ( রেঞ্জ নয় কিন্তু ) । যখনই এই B সেটটি রেঞ্জের সেটটির সাথে মিলে যাবে একেবারেই,তখন আমরা ফাংশনটিকে সার্বিক বলবো! 😀
দু’টি টিকাঃ
১) এক-এক এবং সার্বিক না হলে কোনো ফাংশন কে বিপরীত ফাংশনে রুপান্তর করা যায়না। কারণ, বিপরীতে রুপান্তর করা হয়ে গেলে তা আর ফাংশনই থাকেনা! গ্রাফ এঁকে ব্যাপারটি বুঝার চেষ্টা করো! না পারলে কমেন্ট করবে,তাহলে আমি পরের পর্বে এ ব্যাপারটি আলোচনা করে দিবো।
২) ”সকল ফাংশনই অন্বয়,তবে সকল অন্বয়ই ফাংশন নয়। ”
আজ এই পর্যন্তই!



ho vala hoise.. dst..:)
চমৎকার হয়েছে ভাইয়া
অনটু ফাংশন এবং বিপরীত ফাংশন নিয়ে আলোচনা করলে ভাল হতো।
দু’টো নিয়েই লিখা হয়েছে এখানে।
অসম্ভব ভালো।
খুব ভালো হয়েছে, আমি অনেক কিছু বুজতাম না এখন বুজেছি। thanks for the post
Super Cool 😀 আমি এখন এই সাইটের নিয়মিত পাঠক । <3
অনেক ধন্যবাদ ।।
অসাধারন।
ধন্যবাদ আপনাকে,,,
অসাধারণ