হ্যালো।
আজকে আমরা কম্বিনেশনের একটি প্রব্লেম নিয়ে আলোচনা করব।
প্রব্লেমঃ ধর, তোমাকে একটি শব্দ বানাতে হবে। এটার জন্য তুমি কোন letter EXACTLY কতবার ব্যবহার করতে পারবে তা বলা আছে। এখন তোমাকে বলতে হবে কতভাবে তুমি এই letter গুলা ব্যবহার করে word বানাতে পারবে। তবে একটা রেস্ট্রিকশন আছে (মুহাহাহাহা!!), অবশ্যই একটি letter এর শেষেরটা ব্যবহার করার আগে alphabetically তার আগের সবগুলা letter শেষ করে আসতে হবে। অর্থাৎ, শেষের B বসানোর আগে অবশ্যই সবগুলা A বসানো থাকতে হবে, শেষের C বসানোর আগে অবশ্যই সবগুলা A আর B বসানো থাকতে হবে এমন। ধরি, ২টা A, ৩টা B এবং ২টা C আছে। তো, AABBBCC, ABBABCC, ABBACBC, BABABCC এগুলা valid কিন্তু ABBBACC, BBBAACC, BBACCBA এগুলা valid হবে না।
একটি উদাহরণ দেখতে দেখতে আমরা প্রব্লেমটি সল্ভ করব।
ধরি, ৩টি A, ৩টি B আর ৩টি C দেয়া আছে।
শুরু করার আগে একটা general knowledge বলে নেই। এক লাইনে যদি n টা বস্তু থাকে, তাহলে ঐ লাইনে পরবর্তী বস্তু রাখার জন্য n+1 টা জায়গা থাকবে। nটা বস্তুর প্রতি দুটির মাঝখানের একটি জায়গা অর্থাৎ n-1টা জায়গা আর লাইনের শুরুতে এবং শেষে আরো দুটি জায়গা। মোট n+1টা জায়গা।
শুরুতে আমাদের কাছে বসানোর মত একটি জায়গা আছে। এখানে আমরা শেষের A টি বসিয়ে ফেলি। বসানো যাবে 1 ভাবে। এখন আমাদের কাছে জায়গা আছে ১টি (নিচের ছবিতে দেখ)।
এখানে আরেকটি A বসানো যাবে 1 ভাবে। 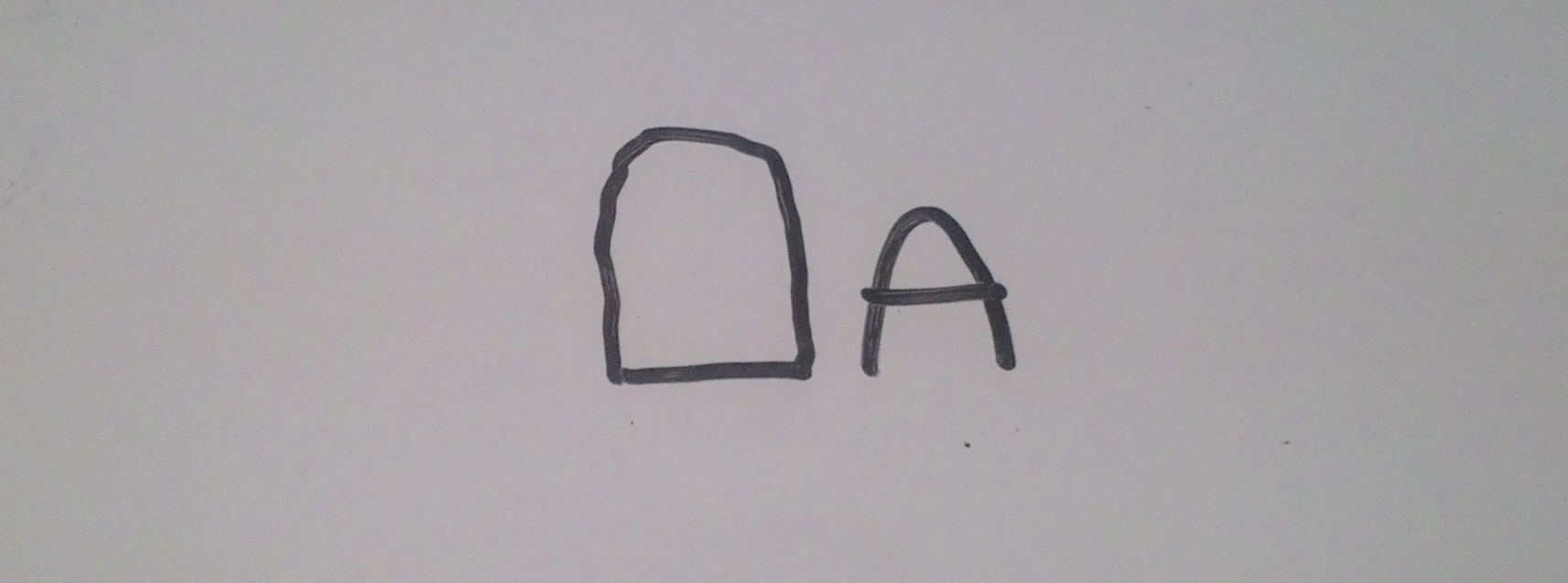 (অনেকের মতে হতে পারে যে A এর পরেও তো আরেকটি জায়গা তৈরি হওয়ার কথা। সেটি আমরা কেন নিচ্ছি না? fix করা A এর পরেওতো একটি জায়গা আছে! ওইখানে আবারো A বসালে তো আর আগেরটি “শেষের” A থাকছে না তাই সেটি বাদ। চিত্র দেখে ক্লিয়ার হতে পার। )
(অনেকের মতে হতে পারে যে A এর পরেও তো আরেকটি জায়গা তৈরি হওয়ার কথা। সেটি আমরা কেন নিচ্ছি না? fix করা A এর পরেওতো একটি জায়গা আছে! ওইখানে আবারো A বসালে তো আর আগেরটি “শেষের” A থাকছে না তাই সেটি বাদ। চিত্র দেখে ক্লিয়ার হতে পার। )
এখন জায়গা তৈরি হবে দুইটি (নিচের চিত্রের মত)।
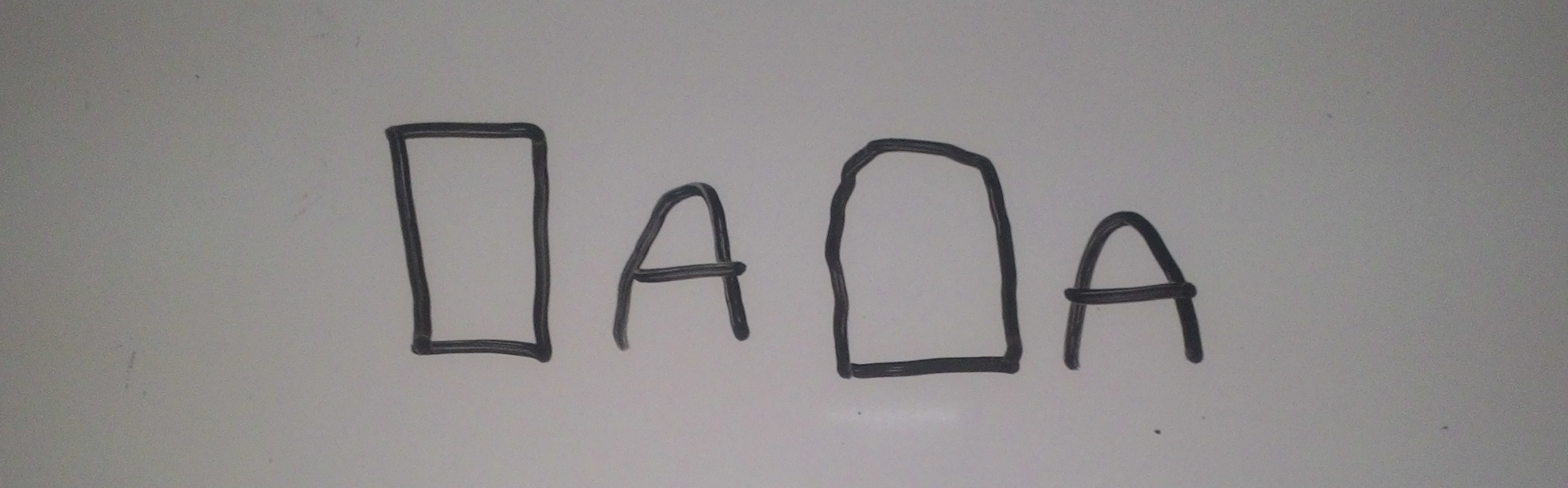
সুতরাং, আরেকটি A বসাতে পারব 2 ভাবে।
সুতরাং,গণণার গুণন বিধি অনুযায়ী, এইদুটি A বসানো যাবে 1*2 উপায়ে।
কিন্তু প্রথমে যে A টি fix করেছি (শেষের A হিসাবে) সেটি বাদে বাকি দুইটি A কে আসলে দুইটি আলাদা জিনিষ চিন্তা করে যত ভাবে সাজানো যায় সেই মান বের করেছি। কিন্তু A দুটি আসলে identical। তাই এই সংখ্যাকে 2! দিয়ে ভাগ করতে হবে। সুতরাং, সাজানোর সংখ্যা (1*2) / 2!.
(এখন পর্যন্ত এই হিসাবটাকে আজাইরা বলে মনে হতে পারে কিন্তু পরের letter এ যাওয়ার সময় বুঝব যে এই ভাবেই আগাতে হবে)
তো, A নেয়া শেষ।
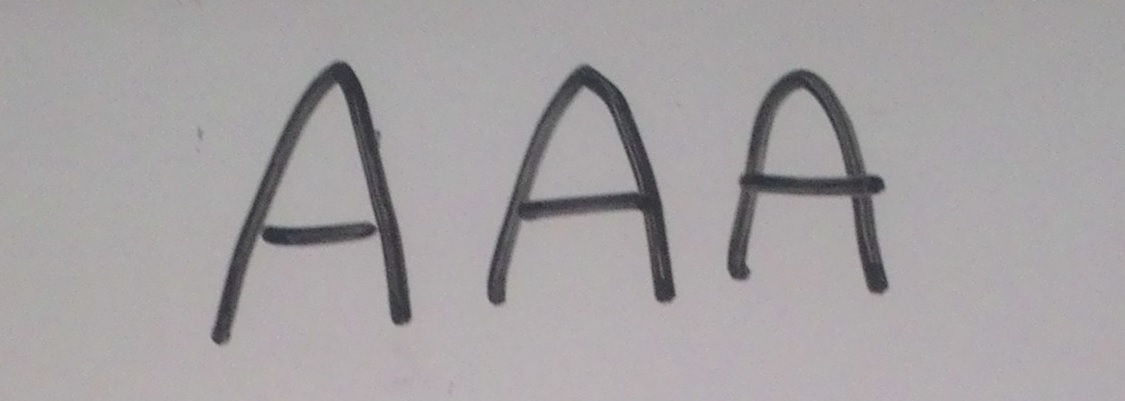
এখন আমরা যাই নেই না কেন, বাকি সবগুলা শেষ করার আগে অর্থাৎ C শেষ করার আগে B শেষ করতে হবে। তাই সবার শেষে, শেষের B টি নিয়ে নেই।
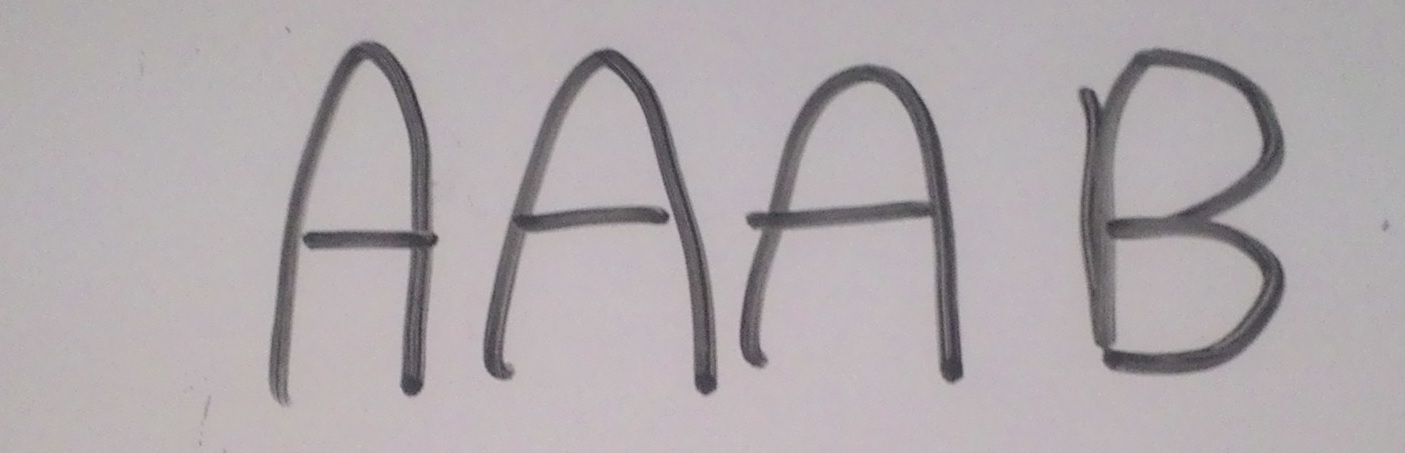
এখন একটু চিন্তা করে বলি তো, শেষের B টির আগের B টি বসানো যাবে কয়টি জায়গায়?
৪টি জায়গায়। যেহেতু শুধুমাত্র শেষের A এর উপরে restriction ছিল যে সেটি B এর আগে শেষ হতে হবে, সুতরাং, এখন আমরা বাকি B গুলাকে A গুলার মাঝখানেও বসাতে পারব। আগের ৩টি A এবং শেষের fix করা B এর খোপে খোপে আমরা ৪টি জায়গা পাই যেখানে B বসানো যাবে। (যারা ভাবছ যে fix করা B এর পরেও তো একটি জায়গা আছে! ওইখানে আবারো B বসালে তো আর আগেরটি “শেষের” B থাকছে না তাই সেটি বাদ। চিত্র দেখে ক্লিয়ার হতে পার।)

এখন একটু স্লো যাই। একটু ভেবে দেখি যে, আগের B টি আগের ৪টি ঘরের যে ঘরেই বসাই না কেন, এখনকার B বসানোর জন্য আমাদের কাছে ঠিক ৫টি জায়গা তৈরি হবে। চিত্র দেখে নাও ঠিক মত বুঝার জন্য। উপরের B টি বসানোর জন্য যে ৪টি জায়গা ছিল, তাদের প্রত্যেক জায়গায় বসালে বিন্যাস আর ভেতরের ফাকা জায়গা কেমন হবে তা বুঝার জন্য নিচের ৪টি চিত্র দেখ এবং আগের চিত্রের সাথে মিলিয়ে নাও।
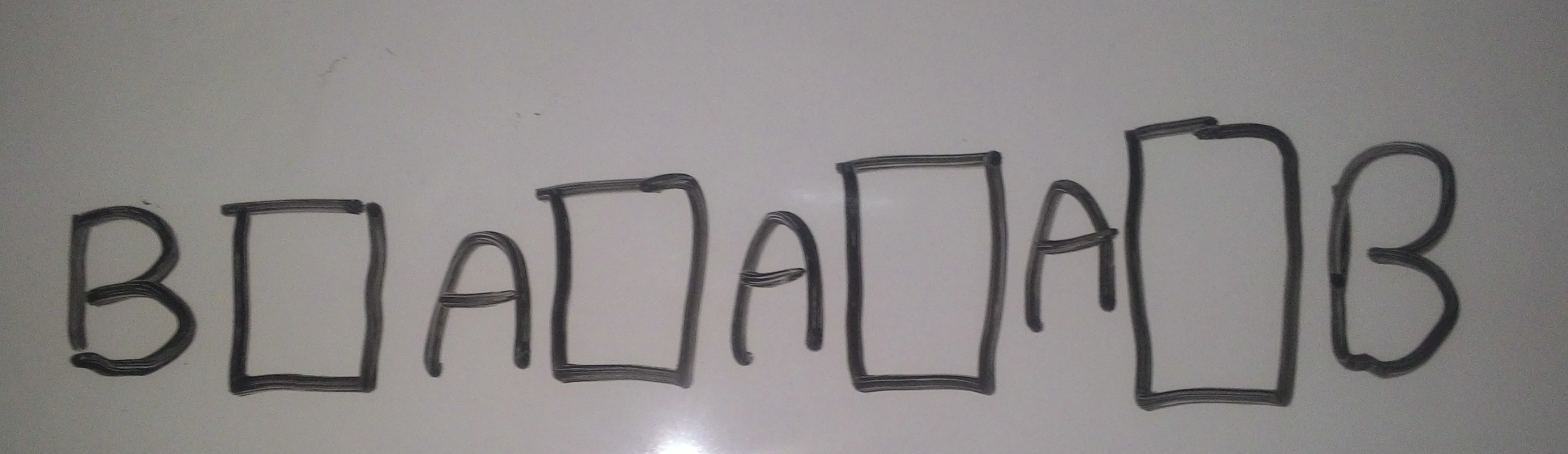

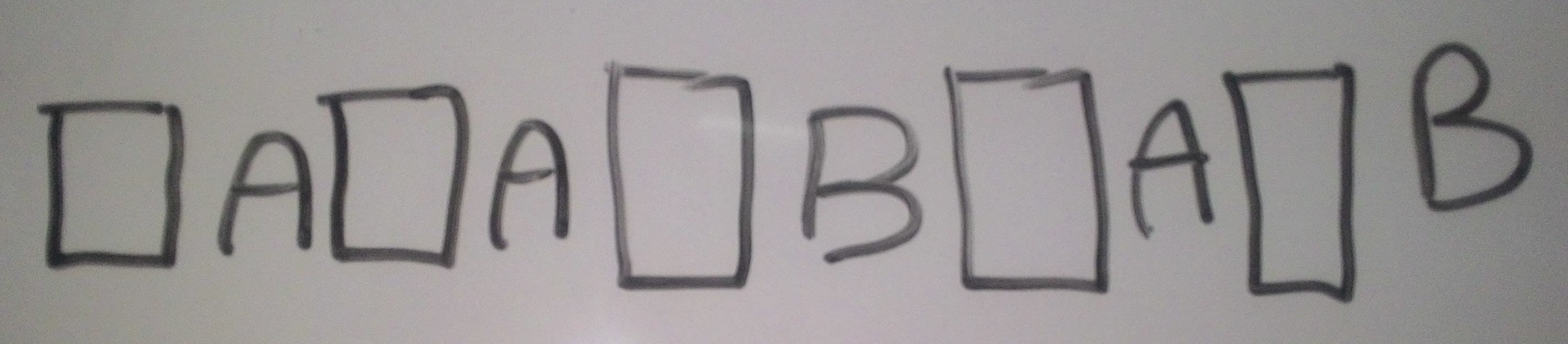

এইটুক যদি বুঝে থাকো, তাহলে বাকিটুকু হয়ত নিজে চিন্তা করেই বের করতে পারবে। এখন আমরা আগের মতই আগাব।
এখন আরেকবার B বসানোর জন্য আছে ৫টি জায়গা। সুতরাং, আপাতত B বসানোর সংখ্যা বের হল, (4 x 5)। কিন্তু B গুলা তো identical, এর মধ্যে শুধু শেষের টা fixed। তাই উক্ত সংখ্যাকে (3-1)! অর্থাৎ 2! দিয়ে ভাগ করা লাগবে। অর্থাৎ, B সাজানোর সংখ্যা দাঁড়ায় (4 x 5) / 2!.
এখানে ছোট্ট একটি পার্টের আন্সার তো অল্রেডি বের হয়ে গেল। গণণার গুণন বিধি অনুযায়ী, ৩টি A আর ৩টি B নিয়ে মোট word হয় [(1 x 2) / 2!] x [(4 x 5) / 2! ]
আচ্ছা এখন নিচের ধাপ দেখার আগে, তুমিই একবার চিন্তা করে হাতে কলমে হিসাব করে চেষ্টা করে দেখ, আশা করি নিজেই পেরে যাবে।
এক বার চেষ্টা = এক ইউনিট রেস্পেক্ট
এখন, আগের বারের মতই শেষে একটি C fix করে ফেলি।
পরবর্তি C বসানোর জন্য জায়গা থাকে ৭টি।
আগের C টি যেখানেই বসাই না কেন, এখন আবার C বসানোর জন্য জায়গা দাঁড়ায় ৮টি।
সবকিছু আগের বারের মত করেই C সাজানোর সংখ্যা দাঁড়ায় (7 x 8) / 2!.
সুতরাং সকল কেরামতি শেষ করার পর ৩টি A, ৩টি B এবং ৩টি C নিয়ে রেস্ট্রিকশন মেনে মোট word বানানো যায়, [ (1 x 2) / 2! ] * [ (4 x 5) / 2! ] x [ (7 x 8) / 2! ] টি।
!!!!!!শ্যাষষষষষষষষষষষ!!!!!!
এখন দেখি, একটা কম্পিউটার প্রোগ্রাম তৈরি করার জন্য অথবা পুরো ব্যাপারটিকে কিভাবে generalize করতে পারি।
উপরের উত্তর টি আবার লিখিঃ ( 1 x 2 x 4 x 5 x 7 x 8) / (2! x 2!).
লক্ষ্য করি যে লবে ৩, ৬ আর ৯ গুণ থাকলেই তা 9! হয়ে যেত। বিষয়টি একটু analysis করি।
Permutation এর সূত্র তো গণনার গুণন বিধি থেকেই আসছে। আর আমরা সবসময় সবগুলো থেকে সবগুলো letter ই নিয়ে আসছি। তাহলে কেন মাঝখান থেকে ৩, ৬ আর ৯ missing!!
Sounds like a job for ব্যোমকেশ again!!
ব্যাপারটা হল যে, আমরা প্রথমেই একটি A, একটি B, একটি C বসিয়ে নিয়েছি। সাধারণ বিন্যাস চিন্তা করলে সেগুলো বসানো যেত যথাক্রমে ৩টি, ৬টি ও ৯টি ঘরে যা আমরা বাদ দিয়েছি।
এক কাজ করি তাহলে! হরে আর লবে এই ৩, ৬, ৯ গুণ দিয়ে দেই। তাহলে আমাদের এখনকার রেজাল্ট আসবেঃ 9! / (3 x 6 x 9) / (2! x 2!)
এখন আবার আরেক ভেজাল! এই ৩,৬,৯ আসলে কি না বুঝলে তো অন্য input এর জন্য সল্ভ করতে পারব না।
আমরা এখন আগে শেষের letter না বসিয়ে শুরু থেকে চিন্তা করব।
প্রথম ২টি A বসানোর পর শেষের টি বসানোর জায়গা হয় ৩টি। কিন্তু আমরা এটিকে ফিক্স করে নিয়েছি তাই এখান থেকে ৩ বাদ গিয়েছিল। দেখি এই তিন কিভাবে আসছে।
এটা একটা general knowledge এর বিষয় যে এক লাইনে nটা বস্তু রাখলে, তাদের মাঝে এবং আগে পিছে মোট n+1 টা জায়গা তৈরি হবে। কাম শ্যাষ!!!
তাহলে শেষের A টি বসানোর জায়গা = ( (A এর সংখ্যা – 1) + 1 ) টি অর্থাৎ A এর সংখ্যা।
ঠিক একই ভাবে, শেষের B টি বসানোর জায়গা ( (A,B এর সংখ্যা – ১) + ১) অর্থাৎ A,B এর মোট সংখ্যা।
And So on…
তাহলে আমাদের generalized solution হলঃ
(মোট letter এর সংখ্যা) / [( A এর সংখ্যা * (A+B) এর সংখ্যা * (A+B+C) সংখ্যা * … … … ) * ( (A এর সংখ্যা – 1)! * (B এর সংখ্যা – 1)! * (C এর সংখ্যা – 1)! * … … … )]
আইডিয়া টি বুঝতে পারলে এই প্রব্লেমটি সল্ভ করে ফেলঃ
http://www.lightoj.com/volume_showproblem.php?problem=1226
আর কিছু বুঝতে অসুবিধা হলে, জিজ্ঞেস করতে পার।
ধন্যবাদ।
মোঃ শাহরিয়ার হোসেন সজীব

Thanks for making it easier to understand 🙂