নেগেটিভ সাইকেল খুজে বের করা – বেলম্যান ফোর্ড

আগের পর্বে আমরা দেখেছি কীভাবে ডায়াক্সট্রার এলগরিদম ব্যবহার করে গ্রিনগটসের সব ভল্টে যাওয়ার সর্বনিম্ন দুরত্ব বের করা যায়। আমাদের এত সহজে তাদের সব রহস্য জেনে যাওয়া গবলিনদের পছন্দ হলো না। কারণ কোনো গবলিনই স্বীকার করতে চায় না যে তারা মানুষের সাহায্য নিয়েছে! তারা নতুন এক সমস্যা সৃষ্টি করলো। যদিও বলা বাহুল্য, তারা এ কাজ সাহায্য নিয়েছে মানুষেরই তৈরী আরেক এলগরিদমের, যার নাম বেলম্যান ফোর্ড। 

তো তারা করলো কী, এবার তাদের গ্রাফে এমন কিছু ট্র্যাক (রাস্তা) যোগ করলো যেগুলো দিয়ে গেলে কিনা সময় পিছিয়ে যায়! যার মানে হল, আপনি যদি -৩ মানের একটি এজ দিয়ে যান, তাহলে আপনি তিন মিনিট আগের সময়ে ফিরে যাবেন! এবার তারা জানতে চাইলো আপনি বলতে পারবেন কি না ০ নাম্বার নোড থেকে সব নোডে যাওয়ার সর্বনিম্ন সময় কত?

প্রথমে, আমরা সমস্যাটিকে গ্রাফে রূপান্তর করে নিই। বলা বাহুল্য সমস্যাটা ঠিক আগেরটার মতই। আমাদের কাছে কিছু নোড আছে, আর কিছু কস্ট আছে। আমাদের বলতে হবে ০ থেকে বাকি সব নোডে যেতে মিনিমাম কস্ট কত। এখন শুধু একটাই পরিবর্তন, তা হল, এখন কিছু এজে নেগেটিভ কস্ট আছে। এখানে দুই ধরণের Case হতে পারে। আমাদের গ্রাফ হতে পারে নিচের মতঃ

 

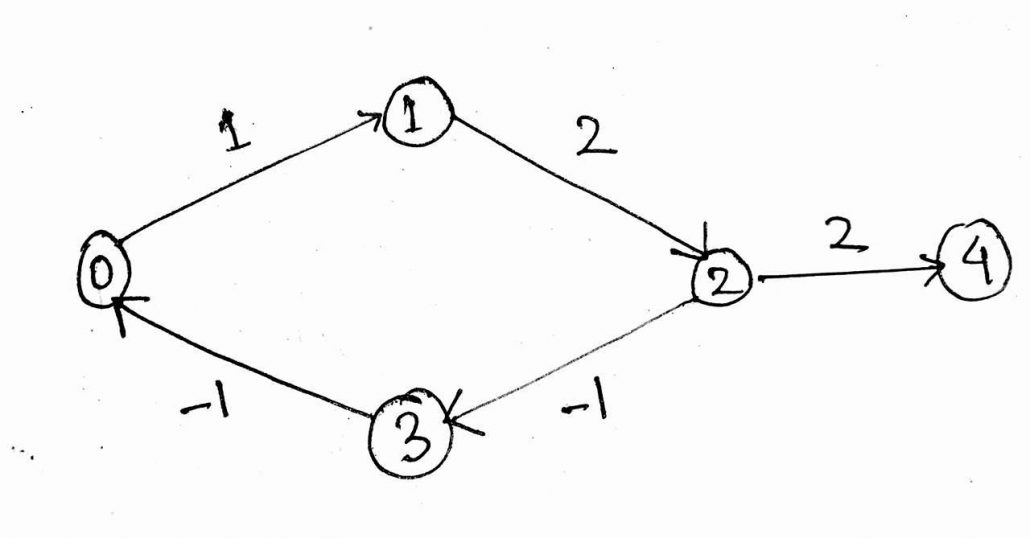
কিংবা আমাদের গ্রাফ হতে পারে নিচের মতঃ

 

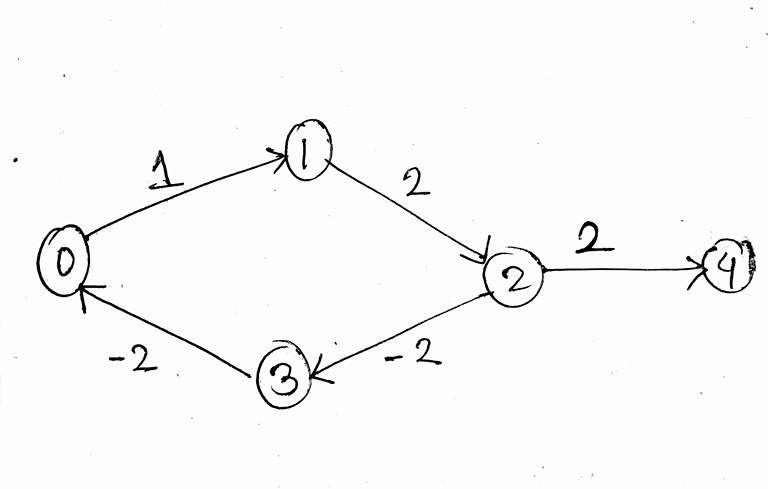
পার্থক্য কী? পার্থক্য হল আগের গ্রাফে কোনো নেগেটিভ সাইকেল নেই। কিন্তু এই গ্রাফে একটি নেগেটিভ সাইকেল আছে (0->1->2->3->0)। ধরো, 0 কে রুট ধরে 4-এ যেতে চাই। আমরা এই নেগেটিভ সাইকেল যতবার ব্যবহার করবো, তত আমাদের সময় কমতেই থাকবে! নেগেটিভ সাইকেলটির টোটাল কস্ট হল -1। তাহলে একবার ব্যবহার করলে সময় কমবে -1, দুইবার করলে কমবে -2। তাহলে তো আমি সারা জীবন এই সাইকেলেই ঘুরতে থাকবো, আর সময়ও কমতে থাকবে। কী মজা!

একারণে এখন আসলে 0 নাম্বার নোড থেকে বাকি সব নোডে যাওয়ার সময়ই নেগেটিভ ইনফিনিটি!

ডায়াক্সট্রার এলগরিদম প্রথম গ্রাফে ঠিক মতই কাজ করবে। সমস্যা হবে দ্বিতীয় গ্রাফে এসে। এই গ্রাফে ডায়াক্সট্রা বার বার আপডেট করতেই থাকবে নেগেটিভ সাইকেলের নোডগুলার জন্য, আর সেটা Infinite Loop হয়ে যাবে। তাই আমাদের এখানে সাহায্য নিতে হবে বেলম্যান ফোর্ডের। বেলম্যান ফোর্ড এলগরিদম যা করে তা হলঃ

• যদি নেগেটিভ সাইকেল থাকে, তাহলে বলে দেয় যে, নেগেটিভ সাইকেল আছে। নেগেটিভ সাইকেল বলতে বুঝাচ্ছি এমন একটি সাইকেল যার টোটাল কস্ট নেগেটিভ।
• যদি নেগেটিভ সাইকেল না থাকে, তাহলে রুট থেকে সব নোডের সর্বনিম্ন দুরত্ব বের করে দেয়।

আমরা সরাসরি বেলম্যান ফোর্ড না শিখে আগে Intuitively কিছু করার চেষ্টা করি। আমাদের গ্রাফে যদি n-টা নোড থাকে, তাহলে আমরা কখন নিশ্চিতভাবে বলতে পারবো যে, u থেকে v-তে যেতে আমরা কোনো একটি নোড দিয়ে একবারের চেয়ে বেশীবার গিয়েছি? যখন আমরা u থেকে v-তে যেতে (n-1)-এর চেয়ে বেশী সংখ্যক এজ ব্যবহার করি।

তাহলে আমরা সমস্যাটাকে এভাবে সমাধানের চেষ্টা করতে পারি। নেগেটিভ সাইকেল বের করার জন্য আমাদের জানতে হবে আমরা n-সংখ্যক এজ ব্যবহার করে আগের চেয়ে কম কস্টে রুট থেকে অন্য কোনো নোডে যেতে পারি কি না। এটা আমরা কীভাবে করতে পারি?

ধরা যাক, আমরা নিচের ইনফর্মেশন সেভ করবো।

int distance[MaxNodes][MaxNodes];

এখানে প্রতিটি distance[i][j] এন্ট্রির অর্থ হল, রুট থেকে i তম নোডে j সংখ্যক এজ ব্যবহার করে যাওয়ার সর্বনিম্ন কস্ট কত। আমরা এই ইনফর্মেশন ব্যবহার করে কী পাথ রিলাক্সেশনের আইডিয়া ব্যবহার করতে পারি? k-সংখ্যক এজ ব্যবহার করে কোনো নোডে যাওয়ার জন্য আমরা যা করবো তা হল, প্রতিটি u->v এজ-এর জন্য দেখবো distance[u][k-1] + cost[u][v] < distance[v][k] কি না।  এর অর্থ হল, k সংখ্যক এজ ব্যবহার করে v-তম নোডে বর্তমানে যে কস্টে আসা যায়, u->v এজটি ব্যবহার করলে তার চেয়ে কম কস্টে আসা যাবে কি না? আর এটি জানার জন্য আমাদের আগে u-তম নোডে k-1 সংখ্যক এজে আসার সর্বনিম্ন কস্ট কত তা জানতে হবে। কন্ডিশনটার মধ্যে আমরা তাই করেছি! তাহলে আমরা এখন সমাধানের আরেকটু কাছে যেতে পারি।

আমরা রুট থেকে প্রতিটা নোডের জন্য 1 থেকে শুরু করে n টা নোড ব্যবহার করে যাওয়ার কস্ট বের করে রাখবো। এরপর দেখবো n নোড ব্যবহার করলেই কস্ট সবচেয়ে কম কি না। যদি তাই হয়, তাহলে অবশ্যই নেগেটিভ সাইকেল আছে। আর যদি তা না হয়, তাহলে প্রতি সারির সর্বনিম্ন মানটাই হল রুট থেকে ওই নোডে যাওয়ার সর্বনিম্ন কস্ট!

এবার তাহলে কোড লেখার চেষ্টা করি। আমরা এজন্য বটম আপ (ইটারেটিভ) এপ্রোচ ব্যবহার করবো।

int distance[1001][1001];
int ans[1001];
struct edges {
    int u, v, cost;
};
vector <edges> edge;
#define INF 1000000000
void detectNegCycle (int root, int n, int E) {
    // root = root
    // n = number of nodes
    // E = number of edges
    // initialize with infinite value
    for (int i=1; i<=n; i++)
        for (int j=1; j<=n; j++)
            distance[i][j] = INF;
    for (int i=1; i<=n; i++) {
        for (int j = 0; j<E; j++) {
            if (distance[edge[j].u][i-1] + edge[j].cost < distance[edge[j].v][i]) {
                distance[edge[j].v][i] = distance[edge[j].u][i-1] + edge[j].cost;
            }
        }
    }
    bool negativeCycle = 0;
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=n; j++) {
            if (distance[i][j] < mn) {
                mn = distance[i][j];
                if (j==n) {
                    negativeCycle = true;
                    break;
                }
            }
        }
        ans[i] = mn;
    }
    if (negativeCycle) printf("Negative Cycle Detected!\n");
    else {
        for (int i=1; i<=n; i++) {
            if (ans[i] == INF) printf("Not reachable. :(\n");
            else printf("From %d to %d with %d\n", root, i, ans[i]);
        }
    }
}

এবার কোডটা বোঝার চেষ্টা করি।

• dis[I][J] দিয়ে বোঝাবে root থেকে I-তে J সংখ্যক নোড ব্যবহার করে যাওয়ার সর্বনিম্ন কস্ট কত। এটা শুরুতে INF দিয়ে ইনিশিয়ালাইজ করে নিতে হবে।
• ans[I] বোঝাবে root থেকে I-তে যেতে সর্বনিম্ন কস্ট কত।
• আমরা এখানে edges নামের একটা স্ট্রাকচার ব্যবহার করেছি। এটা দিয়ে সব u->v এজ তাদের কস্ট সহ স্টোর করে রাখবো।

• for (int i=1; i<=n; i++) {
       for (int j = 0; j<E; j++) {
          if (distance[edge[j].u][i-1] + edge[j].cost < distance[edge[j].v][i]) {
              distance[edge[j].v][i] = distance[edge[j].u][i-1] + edge[j].cost;
          }
      }
  }

  এখানে i দিয়ে ১ থেকে n পর্যন্ত ইটারেট করছি i সংখ্যক এজ ব্যবহার করে যাওয়ার জন্য। আর ভেতরের j লুপ দিয়ে প্রতিটা এজ দিয়ে পাথ রিলাক্সেশন করার চেষ্টা করছি।

• for (int i=1; i<=n; i++) {
     for (int j=1; j<=n; j++) {
         if (distance[i][j] < mn) {
              mn = distance[i][j];
              if (j==n) {
                  negativeCycle = true;
                  break;
              }
          }
      }
      ans[i] = mn;
  }

  এখানে প্রতিটা নোডে যাওয়ার সর্বনিম্ন কস্ট খুজে বের করছি। আর সেই সর্বনিম্ন কস্ট যদি n এজ ব্যবহার করে পাওয়া যায়, তাহলে বলছি যে নেগেটিভ সাইকেল আছে।

• আর শেষে প্রিন্ট করেছি। এটা নিয়ে আর বলার কিছু নাই।

অতঃপর বেলম্যান ফোর্ড

আমরা এখানে প্রায় বেলম্যান ফোর্ড এলগরিদমের মতই কাজ করেছি। শুধু একটা কাজ বেশী করে রেখেছি, যা না করলেও হত।

for (int i=1; i<=n; i++) {
     for (int j = 0; j<E; j++) {
        if (distance[edge[j].u][i-1] + edge[j].cost < distance[edge[j].v][i]) {
            distance[edge[j].v][i] = distance[edge[j].u][i-1] + edge[j].cost;
        }
    }
}

খেয়াল কর, আমরা এখানে বটম আপ এপ্রোচ ব্যবহার করেছি, তাই i-লুপে প্রতিবার i-সংখ্যক এজ ব্যবহার করে কোথাও যাওয়ার জন্য আমরা (i-1) সংখ্যক এজ ব্যবহার করে যেসব মান পাওয়া যায় সেগুলো ব্যবহার করছি।

আমরা এবার distance[node][i]-এর ডেফিনিশন একটু বদলে দিই। distance[node][i] এখন বূঝাবে রুট থেকে node-এ যেতে সর্বোচ্চ i সংখ্যক এজ ব্যবহার করলে কস্ট কত হবে? খেয়াল কর, আমরা এখানে সর্বোচ্চ i-সংখ্যক এজ ব্যবহার করতে চাচ্ছি। তাহলে বলা বাহুল্য, আমাদের j-লুপের ভেতরে আরেকটি 0 থেকে i-1  পর্যন্ত লুপ চালাতে হবে।

for (int i=1; i<=n; i++) {
     for (int j = 0; j<E; j++) {
        for (int k=0; k<= i-1; k++) {
            if (distance[edge[j].u][k] + edge[j].cost < distance[edge[j].v][i]) {
                distance[edge[j].v][i] = distance[edge[j].u][k] + edge[j].cost;
            }
        }
    }
}

এখন আমরা সর্বোচ্চ i-সংখ্যক এজ ব্যবহার করলে সর্বনিম্ন কস্ট কত হবে, তা বের করলাম। কিন্তু আমরা তো কাজ কমাতে চাইছিলাম! তা করতে গিয়ে কি না কাজ আরও বাড়লো। আসলে কাজ না কমলেও এখন একটা অবজার্ভেশন আমাদের সহায়তা করবে। খেয়াল করে দেখো, আমরা যেহেতু বটম আপ এপ্রোচ ব্যবহার করেছি, তাহলে আমরা সবসময় এন্সার পাচ্ছি i-থেকে কম সংখ্যক এজ ব্যবহার করা ভ্যালুগুলো থেকে। আর এসবের মধ্যে সব ভ্যালু আমাদের দরকারও নেই। আমরা যদি এখন পর্যন্ত সবচেয়ে কম কস্ট কী আছে তা জানি, তাহলেই কিন্তু হয়ে যায়।

তাহলে আমরা যা করতে পারি তা হল distance-এর ডেফিনিশন আবার বদলে দিই। এখন distance[node]-এর মানে হল রুট থেকে node-এ যেতে সর্বনিম্ন কত খরচ হয়। কতটা এজ ব্যবহার করবো, সেটা আমরা আর সেভ করে রাখবো না। তাহলে এখন আমাদের ans অ্যারেটাও আর দরকার নেই! এবার তাহলে কোডটা লিখে ফেলা যাক।

int distance[1001];
struct edges {
    int u, v, cost;
};
vector <edges> edge;
#define INF 1000000000
void bellman_ford (int root, int n, int E) {
    // root = root
    // n = number of nodes
    // E = number of edges
    // initialize with infinite value
    for (int i=1; i<=n; i++)
        for (int j=1; j<=n; j++)
            distance[i] = INF;
    // ei loop cholbe n-1 porjonto
    for (int i=1; i<n; i++) {
        for (int j = 0; j<E; j++) {
            if (distance[edge[j].u] + edge[j].cost < distance[edge[j].v]) {
                distance[edge[j].v] = distance[edge[j].u] + edge[j].cost;
            }
        }
    }
    // niche ber korbo negative cycle. ei loop cholteche n edge use korar jonno
    bool negativeCycle = 0;
    for (int j = 0; j<E; j++) {
        if (distance[edge[j].u] + edge[j].cost < distance[edge[j].v]) {
            distance[edge[j].v] = distance[edge[j].u] + edge[j].cost;
            negativeCycle = true;
            break;
        }
    }
    if (negativeCycle) printf("Negative Cycle Detected!\n");
    else {
        for (int i=1; i<=n; i++) {
            if (ans[i] == INF) printf("Not reachable. :(\n");
            else printf("From %d to %d with %d\n", root, i, ans[i]);
        }
    }
}

এখানে কমেন্টে মোটামুটি বলা আছে কী করেছি, তাও সংক্ষেপে বলে রাখি।

• for (int i=1; i<n; i++) {
          for (int j = 0; j<E; j++) {
              if (distance[edge[j].u] + edge[j].cost < distance[edge[j].v]) {
                  distance[edge[j].v] = distance[edge[j].u] + edge[j].cost;
              }
          }
      }

  এই লুপে আমরা পাথ রিলাক্সেশন করতেছি আগের মতই। কিন্তু এবার লুপ চলছে n-1 পর্যন্ত।

• for (int j = 0; j<E; j++) {
      if (distance[edge[j].u] + edge[j].cost < distance[edge[j].v]) {
          distance[edge[j].v] = distance[edge[j].u] + edge[j].cost;
          negativeCycle = true;
          break;
      }
  }

  যেহেতু distance অ্যারেতে আমাদের এখন পর্যন্ত সর্বোচ্চ n-1 এজ ব্যবহার করা পথগুলোর ভ্যালু আছে।  তাহলে এবার যদি কোনো পাথ রিলাক্সেশন হয়, তাহলেই আমরা নিশ্চিতভাবে বলতে পারি যে, এখানে নেগেটিভ সাইকেল আছে।

তো এই ছিল বেলম্যান ফোর্ড। এর কমপ্লেক্সিটি এনালাইসিস বেশ সোজা। V-লুপের মধ্যে একটি E-লুপ। তাহলে কমপ্লেক্সিটি হল O(VE)।

V = নোডের সংখ্যা

E = এজের সংখ্যা

বেলম্যান ফোর্ড এলগরিদমের ভিজুয়ালাইজেশন

 

বেলম্যান ফোর্ড দিয়ে করা যায় এমন কিছু সমস্যা

LightOJ 1074 – Extended Traffic

 

গবলিনরা এখন কেমন বোধ করছে? জানতে চোখ রাখুন স্বশিক্ষার ওয়েবসাইটে। 😉