সবাইকে সালাম। আমাদের আজকের পর্বটা প্রোগ্রামিং এবং জ্যামিতি নিয়ে তৈরী করা হয়েছে,তবে যে কেউ চাইলে কিংবা আগ্রহ থাকলে এটা পড়তে পারো। LightOJ অনলাইন জাজের কথা মনে হয় অনেকেই শুনে এসেছো। না শুনে থাকলেও সমস্যা হবেনা।
আজকের আলোচ্য সমস্যাটা হচ্ছেঃ
” তোমাকে একটা ধাতব রড দেয়া থাকবে। এটাতে তাপ প্রয়োগ করলে এটা দৈর্ঘ্যে বাড়তে থাকে। এর আদি দৈর্ঘ্য যদি L হয় , তাপমাত্রা সহগ যদি C হয় আর তাপমাত্রা যদি n ডিগ্রী সেলসিয়াস বাড়ানো হয়,তাহলে নতুন দৈর্ঘ্য হবে:
সমস্যাটাতে তোমাকে n,C,L এর মানও দেয়া থাকবে। তোমাকে যেই জিনিসটা বের করতে হবে,তা নিচের ছবি দেখলেই বুঝতে পারবেঃ
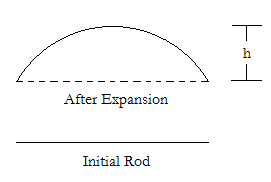
Initial Rod এর দৈর্ঘ্য ছিলো L
After Expansion , রডটার দৈর্ঘ্য হলো L’
রডটাকে আমি একটা দেয়ালের মাঝে যদি রেখে দিই,দেয়ালটার প্রস্থ যদি রডটার আদি দৈর্ঘ্যের সমান হয়,তাহলে এটা আর প্রসারিত না হয়ে বাঁকা হয়ে উপরের দিকে উঠে যাবে। বাঁকা হয়ে উপরের দিকে উঠলে,ছবিতে h এর মান কত হবে সেটাই আমাদের বের করতে হবে।
সমাধানঃ
প্রথমেই আমরা একটি সাবপ্রব্লেম সল্ভ করে ফেলবো। Expansion টা সুষম হওয়ায় রডটা এমনভাবেই বাঁকাবে যেন এটা একটা বৃত্তের অংশ হয় এবং একটা Valid বৃত্তচাপ গঠন করে। তাহলে এক কাজ করি, পুরো ব্যাপারটাকে বৃত্তে নিয়ে গিয়ে কল্পনা করে ফেলি। তারপর মূল সমস্যায় ফেরত আসা যাবে।
ছবিঃ
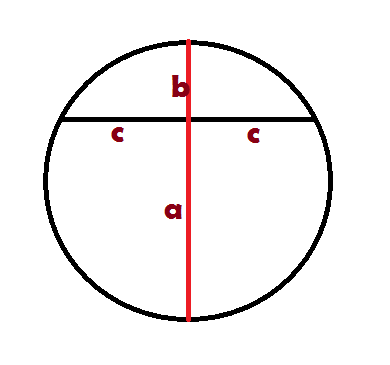
এই ছবিটায় 2c হচ্ছে আমাদের রডটা ( তাপ প্রয়োগ করার আগে) । এই 2c অংশটার ঠিক উপরে যতটুক বৃত্তচাপ আছে,সেটা হচ্ছে তাপ প্রয়োগের পরের অবস্থা। আর b হচ্ছে h ।
a+b = বৃত্তের ব্যাস,এইটুক জানলেই হবে।
বৃত্তের আপাতত এতটুক অবস্থা থেকে আমাদের বৃত্তটার ব্যাসার্ধ (r) কোনোভাবে বের করা যায় কিনা,সেটা দেখতে হবে।
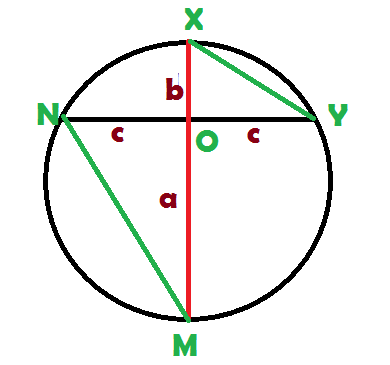
ত্রিভুজ NOM এবং ত্রিভুজ OXY পরস্পর সদৃশকোণী ত্রিভুজ। ( কেন ? কারণ NOM=XOY=90 Degree , ON=OY তাই OMN=XYO )
তাহলে আমরা বলতে পারিঃ
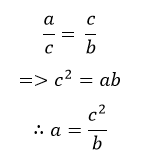
আচ্ছা, a আর b যদি যোগ করে দিই,আমরা ব্যাস পেয়ে যাচ্ছি,তাই না? তাহলে লিখতে পারিঃ
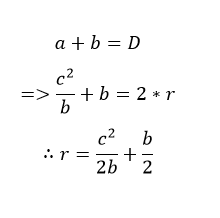
আমরা তাহলে বৃত্তটার ব্যাসার্ধ পেয়ে গেলাম। আমাদের কাজ হচ্ছে এবার এই বৃত্তটার চাপ NXY কেন্দ্রে যে কোণ উৎপন্ন করে,সেটা বের করা। সেটা বের করা আরো সহজ,ছবিটা এঁকে দিলে নিজেরাই বের করে ফেলতে পারবেঃ
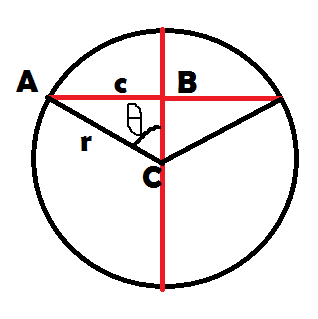
এখানে হাতে আঁকা বিশ্রী থিটার ভ্যালুটা বের করা লাগবে। হালকা পাতলা ত্রিকোণমিতি মেরে দিয়ে এটা বের করে ফেলা যায়।
থিটার মান হবেঃ
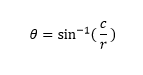
তাহলে , বৃত্তচাপ কেন্দ্রে যে কোণ উৎপন্ন করে,তা হবে এর দ্বিগুণঃ
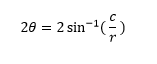
এবার , বৃত্তচাপের দৈর্ঘ্য যদি হয় S , তাহলে আমরা লিখতে পারিঃ
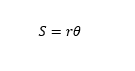
এ পর্যন্ত যা যা পেলাম তা বসিয়ে দিয়ে পাইঃ
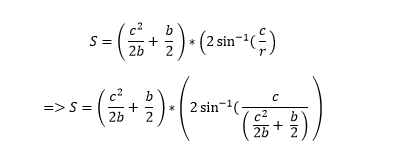
এখন লক্ষণীয় এইযে, S এর মান আমরা শুরুতেই বের করে ফেলতে পারি। সেটা হচ্ছে,S=L’
তাহলে আমরা আবার S এর মান এত কষ্ট করে বের করছি কেন? আমরা আসলে উপরের সমীকরণটা থেকে S এর মান বের করছি না,বের করার চেষ্টা করছি b এর কোন মানের জন্য আমাদের S এর মান L’ এর সমান হয়!
আমরা আবারো আমাদের S বের করার সমীকরণটিতে চোখ বুলিয়ে আসি। খুব ভালোভাবে এই সমীকরণের Variable এবং Constant ভ্যালুগুলোকে আইডেন্টিফাই করে ফেলো!
খেয়াল করে দেখো,আমাদের উপরের সমীকরণটায়ঃ
c = W/2 , যেটা আমরা শুরুতেই জানি!
b = ভ্যারিয়েবল। এটাই আমাদের আসল উত্তর,মানে উচ্চতা H. এটার একটা একটা করে মান বসিয়ে বসিয়ে চেক করতে থাকবো S কত আসে। এই S যদি L’ এর সাথে মিলে যায়,b ( বা H ) এর সেই মানটাই আমাদের উত্তর!
এখন, একটা একটা করে b এর মান বসানোর কোনো মানে হয়না! মানে যদি থাকতো,তাহলে আমরা সমস্যাটাকে এভাবে সমাধানই করতাম না! আমরা এখানে যেই কাজটা করবো,এই ফাংশনটার একটা প্রপার্টি চেক দিবো। এবং এই প্রপারটিটা হচ্ছে বাইনারী প্রপার্টি!
ফাংশনটাকে একটু পরিবর্তন করে ফেলিঃ
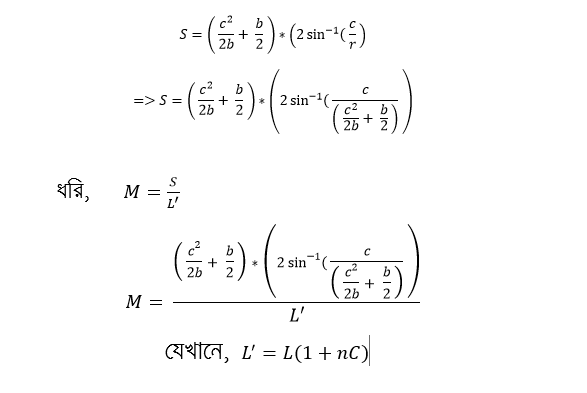
এবার, এই ফাংশনটাকে গ্রাফে বসালে ( n,C,L এদের কিছু ট্রায়াল ভ্যালু ব্যবহার করে আমরা ফাংশনটার চেহারা দেখে আসবো )
যা পাইঃ
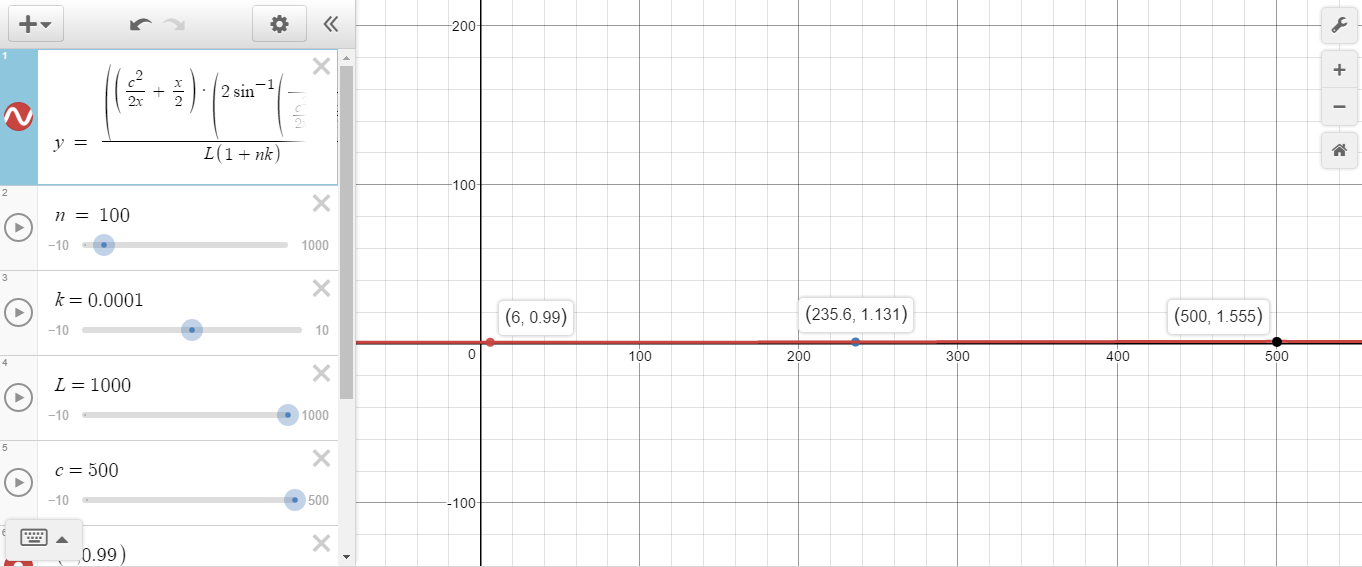
গ্রাফটা অনেকখানি Zoom Out করে নেয়া হয়েছে। না হয় তিনটি বিন্দু দেখানো সম্ভব হচ্ছিলো না।
চমৎকার একটা ব্যাপার হচ্ছে, একটা নির্দিষ্ট রেঞ্জ এর মধ্যে গ্রাফটার Increasing প্রপার্টি আছে! x এর যে মানের জন্যে M এর মান 1 হবে,x এর সেই মানটাই আমাদের উত্তর! কেননা , M = 1 হওয়ার অর্থই হচ্ছে S এবং L’ এক হয়ে যাওয়া। ( ফাংশনটার টার্নারী প্রপার্টিও রয়েছে,খুঁজে বের করা তোমাদের দায়িত্ব!)
তো এবার আর কি! x=0 থেকে x=L এই রেঞ্জের মধ্যে বাইনারী সার্চ চালিয়ে দিলেই আমরা পেয়ে যাবো আমাদের কাঙ্ক্ষিত উত্তর! 😀
কোডঃ
আগে নিজে ১ ঘণ্টা চেষ্টা করো। না পারলে কোডটা দেখোঃ
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <bits/stdc++.h> using namespace std; double W,n,C,L,S; double func(double H) { double r,a; double b=H; double c=L*0.5; r = b/2 + (c*c/(2*b)); a = 2*asin(c/r); return r*a; } int main() { int t; scanf("%d",&t); for(int x=1; x<=t; x++) { scanf("%lf%lf%lf",&L,&n,&C); S=(1.0+(n*C))*L; double st=0.0,en=L,mid; for(int i=0; i<60; i++) { mid=(st+en)/2; if(func(mid)>S) en=mid; else st=mid; } printf("Case %d: %lf\n",x,mid); } return 0; } |
সবাইকে ধন্যবাদ। প্রশ্ন থাকলে জানাতে ভুলো না।
Sadman Sakib
Latest posts by Sadman Sakib (see all)
- Randomized Algorithm – Competitive Programming – Part 2 - February 10, 2020
- Randomized Algorithm – Competitive Programming – Part 1 - December 24, 2019
- গ.সা.গু. এবং ল.সা.গু. – Mind Blown - December 28, 2017
cool ?
বেশ সেক্সি টিউটোরিয়াল
Awesome one. <3
its a fucking problem……but thank you so much Sadman Sakib…You briefed it in such an excellent way. It was awesome to read your article.
clearly its not a 1 minute read, atleast 10 minute. good post (y) thanks a lot ^^
এবার , বৃত্তচাপের দৈর্ঘ্য যদি হয় S , তাহলে আমরা লিখতে পারিঃ S = r (theta) .ভাইয়া এইটা কীভাবে ?
অসাধারণ ভাইয়া
একটি ব্যাপার বুঝলাম না। কেন ২য় লুপ ৬০ বার এক্সিকিউট করতে হবে কেন??
কারণ , বাইসেকশন মেথড এর টাইম কমপ্লেক্সিটি O(logN) , এটাকে অন্যভাবে এভাবে বলা যায়, প্রতি iteration এ এর সল্যুশন ডোমেন ৫০% বা 1/2 হয়ে যায়। তার মানে, আমি যদি ৬০ বার একে ছোট করতে থাকি, সল্যুশন সেট ছোট হতে হতে 1/2^60 এর রেঞ্জে চলে আসবে, যেটা বেশ precise!
তাই আমরা ৬০ বার লুপ চালিয়ে ভালো একটা precision নিশ্চিত করেছি।
” ON=OY তাই OMN=XYO” – where you find this? Can you provide me any proof?
But, both NOM & XOY triangles can be proved similar triangle using inscribed angle theorem.
“Two inscribed angle sharing same arc is equal”.
এই জিনিস টা আমিও বুজি নাই কারন ON = OY হলেও অনেক রকম triangle পসিবল। So we can’t just say “Since ON = OY then OMN = XYO”, After reading your comment Now I feel this a bit.
I am new in this page,but awesome technic.thanks.
Thanks.
You have noted very interesting details! ps decent web site.
এখানে হাইটের আপার বাউন্ড L দেয়া হলো কেন? আর প্রশ্নে L'<=L+L/2 একটা শর্ত ছিল, ম্যাক্সিমাম হাইট L হলে তো তার ব্যাঘাত ঘটে!
side effects of using dapoxetine https://dapoxetine.confrancisyalgomas.com/
off label uses for sildenafil http://cavalrymenforromney.com/
doxycycline 600 mg http://doxycycline.zolftgenwell.org/
hydroxychloroquine withdrawal side effects https://hhydroxychloroquine.com/
cialis 5 mg daily effectiveness https://cialzi.com/
Hi my loved one! I wish to say that this article is amazing, nice written and come with almost
all significant infos. I would like to look extra posts like this
.
thank you so much!! very well explained <3
You really make it seem so easy with your presentation but I
find this topic to be actually something which
I think I would never understand. It seems too complicated and extremely broad for me.
I’m looking forward for your next post, I’ll try to get the hang of it!
Hello! This post couldn’t be written any better! Reading this post reminds
me of my old room mate! He always kept chatting about
this. I will forward this page to him. Pretty sure he will have a good
read. Thank you for sharing!
Definitely believe that which you said. Your favorite reason appeared to be on the web the
simplest thing to be aware of. I say to you, I certainly get annoyed
while people consider worries that they plainly don’t know about.
You managed to hit the nail upon the top and also defined out the whole thing
without having side-effects , people could take a signal. Will likely be back to get more.
Thanks asmr 0mniartist
Hello to all, how is everything, I think every one is getting more from
this web page, and your views are nice in support of new people.
scoliosis
Does your website have a contact page? I’m having a tough time
locating it but, I’d like to shoot you an e-mail. I’ve got some
creative ideas for your blog you might be interested in hearing.
Either way, great site and I look forward to seeing it develop
over time. scoliosis
free dating sites
I like the helpful info you provide in your articles.
I will bookmark your blog and check again here regularly.
I am quite sure I’ll learn plenty of new stuff right
here! Good luck for the next! dating sites
What’s up mates, its wonderful paragraph about cultureand fully defined,
keep it up all the time.
Link exchange is nothing else however it is simply placing the other person’s
website link on your page at proper place and other person will
also do similar in support of you.
In fact no matter if someone doesn’t know then its up to other
viewers that they will assist, so here it occurs.
I am genuinely glad to read this webpage posts which includes tons of helpful data, thanks for providing these statistics.
Hey there would you mind stating which blog platform you’re using?
I’m going to start my own blog soon but I’m having a
tough time making a decision between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your design and style seems different then most blogs and I’m looking for
something unique. P.S Sorry for being off-topic but I had
to ask!
Hello there, I discovered your blog by the use of Google whilst
searching for a comparable topic, your site got here up, it looks good.
I have bookmarked it in my google bookmarks.
Hi there, just become aware of your blog through Google, and found that it is
truly informative. I am gonna be careful for brussels. I will appreciate if you happen to proceed this in future.
A lot of folks might be benefited from your writing.
Cheers!
Hello to every single one, it’s in fact a fastidious for
me to pay a visit this website, it contains useful Information.
Can I simply just say what a comfort to find a person that really
knows what they’re discussing online. You definitely realize
how to bring an issue to light and make it important.
More people really need to check this out and understand this side of the story.
I was surprised that you aren’t more popular because you
certainly have the gift.
이용이유가생기는곳 먹튀검증 안전노리터 go