আশা করি তোমরা সবাই পর্যায় শব্দটি শুনেছো। ত্রিকোণমিতিতে তোমরা ত্রিকোণমিতিক ফাংশনগুলোর পর্যায় পড়েছো বা পদার্থবিজ্ঞানে পর্যায়কাল পড়েছো। কোন “কিছু” যদি নির্দিষ্ট “ব্যবধান” পরপর বারবার আসতে থাকে বা ঘটতে থাকে অর্থাৎ পুনরাবৃত্তি হতে থাকে তখন “কিছু”কে বলে “পর্যায়বৃত্তিক” , “ব্যবধান” টা কে বলে “পর্যায়” আর পুনরাবৃত্তি হওয়ার বৈশিষ্ট্যকে বলে “পর্যায়বৃত্ততা”। 😀
আচ্ছা তাহলে বলো তো, পর্যায়বৃত্তিক ফাংশন কি?
কোন ফাংশনের মানগুলো যদি নির্দিষ্ট ব্যবধান (পর্যায়) পরপর বারবার আসতে থাকে তাহলে সে ফাংশনই পর্যায়বৃত্তিক ফাংশন। যেমনঃ ত্রিকোণমিতিক ফাংশনগুলো (sin, cos, tan ইত্যাদি)।
গাণিতিকভাবে, ডোমেনের অন্তর্ভুক্ত সকল x-এর জন্য যদি
f (x + P) = f (x) হয়,যেখানে P একটিঅশূন্যধ্রুবক, তাহলে f একটি পর্যায়বৃত্তিক ফাংশন।
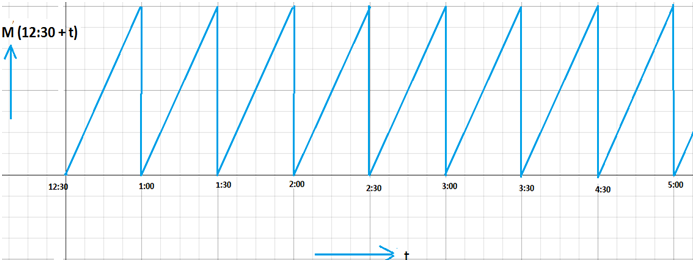
কি কঠিন হল? আচ্ছা, একটা উদাহরণ দেখিঃ ধর, তোমার স্কুলে ক্লাস ১২ টা ৩০ মিনিট এ শুরু হয় এবং প্রতিটি বিষয়ের ক্লাস ৩০ মিনিট করে হয় (আচ্ছা, বল তো প্রতিটি বিষয় ক্লাসকে আমরা কি বলি? :D)। ক্লাসের শুরুর দিকে আমাদের মনের অবস্থা কি রকম থাকে, খুব খারাপ তাই না? 😀 আস্তে আস্তে যখন সময় বাড়তে থাকে তখন ধীরে ধীরে আমাদের আনন্দও বাড়তে থাকে, শেষমেশ যখন ঘণ্টা দেয় তখন আমদের আনন্দ দেখে কে! প্রতিটি বিষয়ের ক্লাসেই কি আমাদের এরকম হয় না? 😀 “সময় যত গভীর হয়, ঘণ্টার শব্দ তত নিকটে আসে।” 😀 আরও একটা ব্যাপার, প্রতি ক্লাসে তোমার মনের অবস্থা একইভাবে পরিবর্তিত হয় ধরে নেই।
এখন ধরি, আমাদের মনের অবস্থা প্রকাশক ফাংশনটা হল M,যা সময়ের সাথে সাথে পরিবর্তিত হয়। সুতরাং, আমাদের ফাংশনটির চলক সময়, t ( মিনিট )। এখন বল তো, এই t এর মান কত থেকে কত পর্যন্ত হতে পারে? অবশ্যই ০ থেকে ৩০ পর্যন্ত (এটাই এর ডোমেন)। আর একটা কথা, আমরা যেহেতু স্কুলে যাওয়ার পর থেকে গণনা করব তাই অবশ্যই ১২ টা ৩০মিনিট থেকে গণনা শুরু করব।
তাহলে আমাদের ফাংশনটা দাঁড়ায়,
M (12:30 + t )এটা হল আমাদের প্রথম বিষয়ের ক্লাসের অবস্থা। এখন বল তো, প্রথম ক্লাসের কোনো এক সময় তোমার মনের অবস্থা যা, ২য় ক্লাসের ওই সময় কি তাই হবে না? তাহলে, ঠিক ৩০ মিনিট পরের ওই সময়ে তোমার মনের অবস্থা আগের মতই হবে। আমরা তাহলে লিখতে পারি,
M ( 12:30 + t + 00:30 ) = M ( 12:30 + t )
ঠিক একইভাবে আরও ৩০ মিনিট পর,
M (12:30 + t + 00:30 + 00:30) = M (12:30 + t + 00:30) = M (12:30 + t)
বা,M (12:30 + t + 2x 00:30) = M (12:30 + t + 00:30) = M (12:30 + t)
সুতরাং , লিখা যায়,
M (12:30 + t) = M (12:30 + t + 00:30) = M (12:30 + t + 2 x 00: 30) = ……….
এখন তুমি যদি বল ২ x ৩০ মিনিট বা ১ ঘণ্টা পর ঘটনাটার পুনরাবৃত্তি হচ্ছে, তাহলে কি হবে না? অবশ্যই হবে। একইভাবে, ১ ঘন্টা ৩০ মিনিট, ২ ঘণ্টা, ……… এই সময়গুলো পরও ঘটনাটার পুনরাবৃত্তি হচ্ছে। তাহলে, এইগুলোও পর্যায়। ব্যাপারটাকে একটু graphically দেখি,
অর্থাৎ,
f (x) = f (x + P) = f (x + 2P) =…………
একটা পর্যায়বৃত্তিক ফাংশনের অনেকগুলো পর্যায় থাকতে পারে (P ,2P,3P,………. এইগুলো সবগুলোই ফাংশনটির পর্যায়)।তাহলে বলা যায়,পর্যায়বৃত্তিক ফাংশন f এর ডোমেনের সকল x এর জন্য,f (x + nP) = f (x), যেখানেP হল ফাংশনটির পর্যায় এবং n হলযেকোন পূর্ণসংখ্যা।
এখন কেউ যদি একটা পর্যায়বৃত্তিক ফাংশন দেখিয়ে আমদের প্রশ্ন করে, বলতো এর পর্যায় কত? তাহলে কি উত্তর দিব? অনেক উত্তর হতে পারে আর সবগুলোই সঠিক। 🙁
চিন্তা নেই, একারণে আমরা যেই পদটি ব্যাবহার করি তা হল “মৌলিক পর্যায়”। এটা আবার কি?
আচ্ছা, আমাদের পর্যায়গুলোর মধ্যে সবচেয়ে ছোট ধনাত্মক একটা পর্যায় আছে না, ওইটাই আসলে “মৌলিক পর্যায়”। পরপর দুইটা পর্যায়ের ব্যাবধানটাই “মৌলিক পর্যায়”। 😀 আমরা এখান থেকে লেখার শেষ পর্যন্ত পর্যায় বলতে মৌলিক পর্যায়কেই বুঝাব।
এবার তাহলে চলো, আমরা আমাদের সবচেয়ে পরিচিত পর্যায়বৃত্তিক ফাংশন ত্রিকোণমিতিক ফাংশনগুলোর পর্যায় বের করার চেষ্টা করি।
আমরা সবাই জানি, ৬টা ত্রিকোণমিতিক ফাংশনের মধ্যে sin, cos, sec, cosec এর পর্যায় 2π বাকি tan, cot এর পর্যায় π. একটু প্রমাণ করে দেখা যাক। আমরা আসলে জানি 2π বা π ব্যাবধি পরে এদের মানগুলো আবার পুনরায় আসতে থাকে। আমরা আসলে প্রমাণ করি যে, এর থেকে ছোট ব্যাবধান পর মানগুলোর পুনরাবৃত্তি হয় না।
f (x) = sec (x)
f (x + P) = sec (x + P) ; where 0 < P < 2π
f (x + P)= f (x)
sec (x + P)= sec (x)
=> 1 / cos (x + P) = 1 / cos (x)
=> 1 / (cos(x)cos(P) – sin(x)sin(P)) = 1 / cos (x)
উভয়পক্ষকেসমানহতেহলে, cos (P) = 1 , sin (P) = 0 হতে হবে।
কিন্তু, ]0, 2π [ ব্যাবধিতে P এর কোন মানের জন্য একইসাথে cos (P) = 1 এবং sin (P) = 0 হতে পারেনা।
সুতরাং , P = 2π
সুতরাং, sec ফাংশন-এর পর্যায় 2π
একইভাবে, বাকিগুলোর পর্যায়গুলোর সত্যতা যাচাই করা যায়।
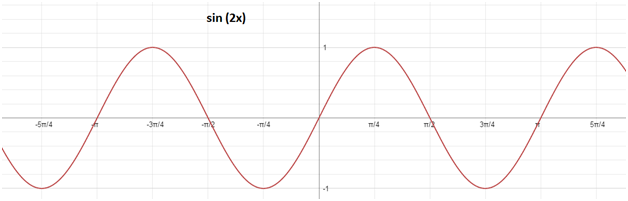
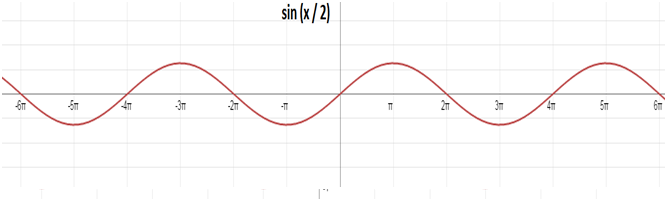
এখন তাহলে বলো তো, 2sin (x)আর sin (2x) আরsin (x/2) এরপর্যায় কত?
2sin (x) এর পর্যায়ও 2π(এর কারণ আমি বলব না, তোমরা চিন্তা করে বের কর :D)
sin (2x) এর পর্যায়π
sin (x / 2) এর পর্যায় 4π
কিভাবে পেলাম? চলো graph থেকে ঘুরে আসা যাক।
এর sin(x) পর্যায় হল 2π। এখন আমরা যখন sin (2x) নিয়ে হিসেব করছি, আগে x এর যেই মানের জন্য 1(ধরি) পেতাম এখন তার অর্ধেক মানের জন্য পাচ্ছি। আবার sin (x / 2) এর বেলায় তার দ্বিগুন মানের জন্য 1 পাচ্ছি। sin (2x) আমাদের sin (x) এর চেয়ে দ্রুত মান দিচ্ছে আর sin (x/2) দিচ্ছে ধীরে। আর যে দ্রুত মান দিবে সে অবশ্যই দ্রুত পুনরাবৃত্ত হবে তার মানে তার পর্যায় হবে কম আর যে ধীরে মান দিবে সে পুনরাবৃত্ত হবে ধীরে তার মানে তার পর্যায় হবে বেশি।
এবার একটা ছোট মজার ব্যাপার দেখি।
পর্যায়বৃত্তিক ফাংশনের সংজ্ঞানুসারে,
sin ( m(x) ) = sin ( m(x + P))
আবার, আমরা জানি,
sin ( m(x) ) = sin ( m(x) + 2π )
অর্থাৎ
sin (mx + mP) = sin (mx + 2π)
সুতরাং, mP = 2π
বা, P = 2π/mএখানে m যেকোনো বাস্তব সংখ্যা।
অতএব, sin (mx) এর পর্যায় হবে 2π/m।
তাহলে এবার বলো তো sin (x √2)আর 3sin (3x)এর পর্যায় কত?:D
এবার একটু জটিল (আসলে সহজ :D) ব্যাপার দেখি।
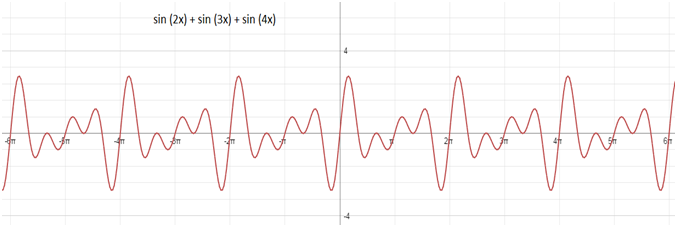
sin(2x) + sin(3x) + sin(4x) এর পর্যায় কত?
অনেকেই হয়ত এতক্ষণে সংজ্ঞা ব্যাবহার করে করা শুরু করে দিয়েছ।করে দেখ। কখনো মাঝপথে থেমে যেও না, তাহলে গণিতের সৌন্দর্য দেখতে পাবে না। 🙂
আচ্ছা, আমরা এবার একটু ৫ম শ্রেণিতে ফিরে যাব। ওখানে আমরা ল.সা.গুআর গ.সা.গু বের করতে শিখেছি তাই না? অনেকের হয়ত প্রশ্ন জাগতে পারে এখানে আবার ল.সা.গু,গ.সা.গু এল কোত্থেকে? আর কথা না বাড়িয়ে চলো দেখি।
আচ্ছা, sin(2x), sin(3x), sin(4x) এর পর্যায়গুলো হল যথাক্রমেπ, 2π/3, π/2তাই না? তার মানে sin(2x) এর মান π ব্যাবধান পরপর ,sin(3x)এর মান 2π/3 ব্যাবধান পরপর , sin(4x) এর মান π/2 ব্যাবধান পরপর পুনরাবৃত্ত হয়।(৩ টা ফাংশনকে যোগ করা হয়েছে।) তার মানে আমরা যদি প্রশ্ন করি প্রশ্নটা হবে এরকম, “তারা একত্রে ন্যুনতম কত ব্যাবধান (পর্যায়) পর পুনরাবৃত্ত হবে?”
আবার ৫ম শ্রেণির একটা গণিতে ফিরে যাই। মনে পরে একটা প্রশ্ন ছিল এরকম,“একটা ঘণ্টা ২ মিনিট পরপর বাজে অপর একটা ঘণ্টা ৩ মিনিট পরপর বাজে, ঘণ্টা দুইটি ন্যুনতম কত সময় পর একত্রে বাজবে?” উত্তরটাও মনে আছে নিশ্চয়ই আমরা বলতাম, “ঘণ্টা দুইটি একত্রে বাজার ন্যুনতম সময় হচ্ছে ২ এবং ৩ এর ল.সা.গু অর্থাৎ ৬।” একটু দেখি,
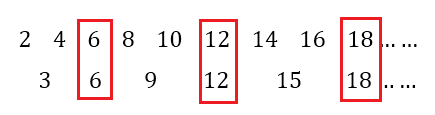 তার মানে ৬ মিনিট পর তারা প্রথম একত্রে বাজবে অর্থাৎ তাদের একত্রে বাজার পর্যায় হবে ৬।
তার মানে ৬ মিনিট পর তারা প্রথম একত্রে বাজবে অর্থাৎ তাদের একত্রে বাজার পর্যায় হবে ৬।
তাহলে এবার আমরা প্রশ্নে ফিরে যাই, বলো তো আমাদের প্রশ্নের উত্তর কি হবে?
হ্যাঁ, ধরতে পেরেছো ,তাদের একত্রে পুনরাবৃত্ত হওয়ার ন্যুনতমব্যাবধান (পর্যায়) হবে π, 2π/3, π/2এর ল.সা.গু অর্থাৎ 2π।কত সহজ তাই না? 😀
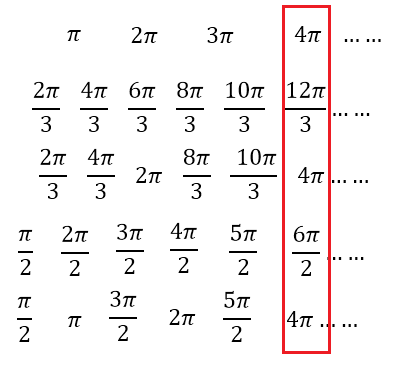
graph টা দেখি চলো।
এবার তাহলে নিচের ফাংশনগুলোর পর্যায় বের কর। 😀
i) cos(x/2) + cos(x) + cos(2x)
ii) tan(x) + tan(2x) + tan(3x)
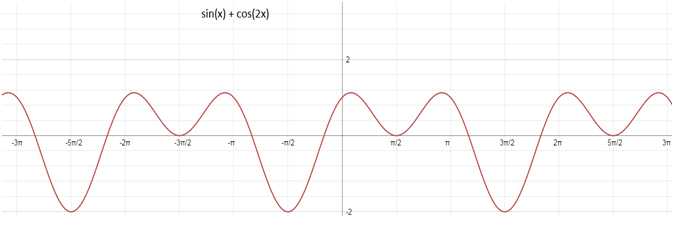
এখন, sin (x) + cos (2x) এর পর্যায় কত?
উত্তরঃ 2π, π এর ল.সা.গু 2π।
graph:
sin(2x) + cos (3x) + tan (x) এর পর্যায় কত?
উত্তরঃ π, 2π/3, πএর ল.সা.গু. 2π।
graph:
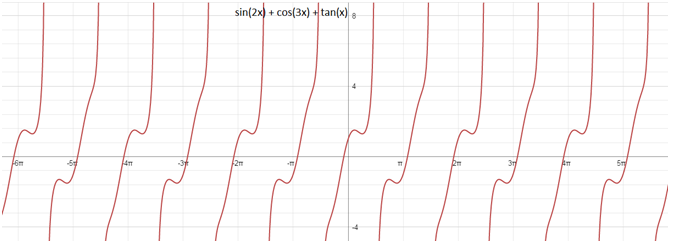
এবার তাহলে নিচের ফাংশনগুলোর পর্যায় বের কর। 😀
i) sin (x/2) – cos(2x) + sin(x)
ii) sin(x) – cos(x/2) – tan(2x)
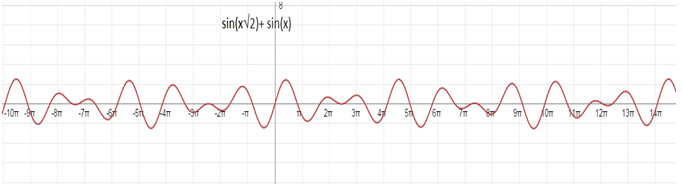
বলো তো sin(x √2) + sin (x) এর পর্যায় কত?অনেকেই হয়ত ভাবছো এ আর এমন কিই বা ব্যাপার। π√2, 2πএর ল.সা.গু.। দাঁড়াও , দাঁড়াও। একটু ভাবো তো।
কিছু খুঁজে পাচ্ছো । graphটা দেখো ।
আসলে এর কোনো পর্যায় নেই। কারণ এমন কোনো সংখ্যা নেই যা একইসাথে 2 এবং√2 দ্বারা নিঃশেষে বিভাজ্য।অর্থাৎ এমন কোনো সংখ্যা নেই যাকে 2 এবং √2দ্বারা ভাগ করলে ভাগফল একটি পূর্ণসংখ্যা হয়। 😀
আজ তাহলে এ পর্যন্তই। আশা করি সবাই বুঝতে পেরেছো। যারা সরল ছন্দিত স্পন্দন পড়েছো তারাও ব্যাপারগুলো লক্ষ্য করে দেখতে পারো। 😀


Osthiiiir
ধন্যবাদ। 🙂
খুব ভাল এবং কার্যকরী একটা পোস্ট …..
আচ্ছা…power function of T.function যেমন , (sinx)^3…or (cosx)^1/2 এগুলোর পর্যায় বের করার পদ্ধতি টাও তো এড করতে পারতি…যাই হোক…
এত সুন্দর একটা লিখার জন্য আবারো ধন্যবাদ…#1141002
oigula next part e add korbo. 😀 Galib, amar roll 1141003 rolltao vuila gesos. -_-
i am a student and i find this interesting… :3
লেখকের সাথে কথা বলতে চাই।
জ্বী, বলুন।
হেই এমেসডব্লু,,,,অসাধারণ লিখেছ।
ভাল লাগল।কনসেপ্ট অনেকটাই ক্লিয়ার হল।