সে অনেক অনেক আগের কথা। খ্রিষ্টপূর্ব ১০০ বছর আগে মিশরে জন্মগ্রহণ করেন ক্লডিয়াস টলেমী। পেশায় তিনি ছিলেন লেখক। আর নেশায় ছিলো জ্যোতির্বিজ্ঞান,গণিত। তিনি পৃথিবীকে কেন্দ্রে রেখে একটি সোলার সিস্টেমের নকশাও এঁকেছিলেন। ভুল হওয়া সত্ত্বেও,তার এই প্রস্তাবনা ভবিষ্যৎ গবেষণায় দারুণ সাহায্য করে!
নবম-দশম শ্রেণীর উচ্চতর গণিত বইতে আমরা টলেমীর উপপাদ্য দেখে এসেছি বা অনেকে “দেখছি”। আজ আমরা টলেমীর সেই বিখ্যাত উপপাদ্যটি নিয়ে কিছু কথা বলবো,একটু ঘেঁটেও দেখবো!
উপপাদ্যটি ছিলোঃ
” বৃত্তস্থ কোনো চতুর্ভুজের বিপরীত বাহুগুলোর অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের যোগফল , চতুর্ভুজটির কর্ণদ্বয়ের অন্তর্গত আয়তক্ষেত্রের ক্ষেত্রফলের সমান। “
বুঝতে অসুবিধা হয়ে থাকলে,নিচের ছবিটা দেখোঃ
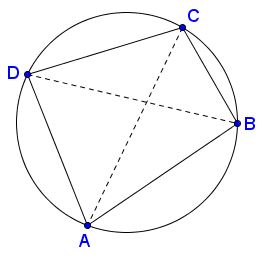
টলেমীর উপপাদ্য বলে কি,আমরা যদি AD * BC আর CD * AB কে যোগ করে দিই,তাহলে তা AC * BD এর সমান হবে। শর্ত একটাই , এইযে চতুর্ভুজটা দেখতে পাচ্ছো,এটাকে একটা বৃত্তের ভিতরে অবস্থিত হতে হবে এমনভাবে,যেন এর চার চারটা শীর্ষ বৃত্তটাকে স্পর্শ করে থাকে। মুখে বললেই তো হবে না,ব্যাপারটা প্রমাণ করে দেখতে হবে। চলো,এই উপপাদ্যর সবচেয়ে সুন্দর অংশটি থেকে ঘুরে আসি। ( আসলে, যেকোনো উপপাদ্যের সবচেয়ে সুন্দর এবং দামী অংশ হচ্ছে তার প্রমাণ। প্রমাণ কখনো বোরিং হয় না,বোরিং করে প্রমাণ করা হয়। :p )
প্রমাণঃ
সর্বপ্রথম যেই কাজটি করবো সেটি হচ্ছে, কোণ ACB এর সমান করে কোণ DCE এঁকে নিবো। ছবিটা দেখো,লাল দাগটি দিয়ে এই কাজটূকুন সেরে ফেলা হয়েছে।
ছবিঃ
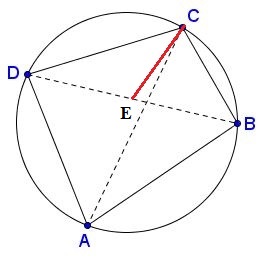
আবার খেয়াল করো,BC এর উপর দণ্ডায়মান বৃত্তস্থ কোণগুলো কে কে? হ্যাঁ ঠিক ধরেছো, কোণ BAC এবং কোণ BDC । অতএব,এরাও সমান।
এবার, ত্রিভুজ ABC এবং ত্রিভুজ CDE এর মাঝে,
কোণ ACB = কোণ DCE
কোণ BAC = কোণ BDC
অতএব, উক্ত ত্রিভুজ দুইটা সদৃশকোণী।
তাহলে এখান থেকে আমরা বলতেই পারি,
CD/CA = ED/BA => CD*BA=AC*ED ———(1)
অনুরূপভাবে,
ত্রিভুজ BCE এবং ত্রিভুজ ACD সদৃশকোণী ত্রিভুজ প্রমাণ করা যায়,চেষ্টা করে দেখো। একই জিনিস,শুধু সিমেট্রিক ব্যাপার!
এখান থেকে বলা যায়,
BC/AC = BE/AD => BC*AD = AC*BE ———(2)
(1) এবং (2) যোগ করে পাই,
BC*AD+CD*AB = AC*(BE+ED) = AC*BD
প্রমাণ করা শেষ। 😀
এবার আসো , আসল কিছু জিনিস দেখি যেগুলো স্কুল কলেজে সুন্দরমতো এভয়েড করে চলে যায়। তোমরা জানো কিনা জানিনা, এই টলেমীর উপপাদ্য দিয়ে চমৎকার ভাবে পীথাগোরাসের উপপাদ্যটা প্রমাণ করে ফেলা যায়। দেখে আসি সময় অপচয় না করেঃ
ধরে নাও, চতুর্ভুজটি একটি আয়তক্ষেত্র। এবার ছবিটি কল্পনা করো,যদি তোমার কল্পনার ছবিটি নিচের মত হয়,তাহলে আমি সার্থক।
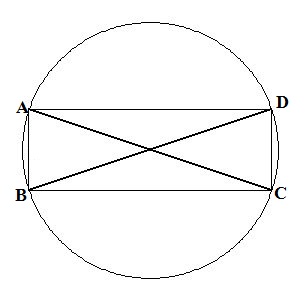
টলেমীর উপপাদ্য কী বলে এই চিত্রে?
টলেমী বলেঃ
AB*DC + AD*BC = AC*BD
যেহেতু এটা একটা আয়তক্ষেত্র,তাই তার বিপরীত বাহুগুলো পরস্পর সমান! তাই বলা চলে, AB=DC এবং AD=BC এমনকি কর্ণদ্বয়ও পরস্পর সমান! তাই,AC=BD.
এই মানগুলোকে উপরের সমীকরণে বসিয়ে দাও,
AB^2 + BC^2 = AC^2
😀
আরেকটি মজার ব্যাপার দেখে আসি। তোমরা কি জানো,বৃত্তস্থ পঞ্চভুজের কর্ণ/বাহু = গোল্ডেন রেশিও?
একটি বৃত্তস্থ পঞ্চভুজ দেখে আসিঃ
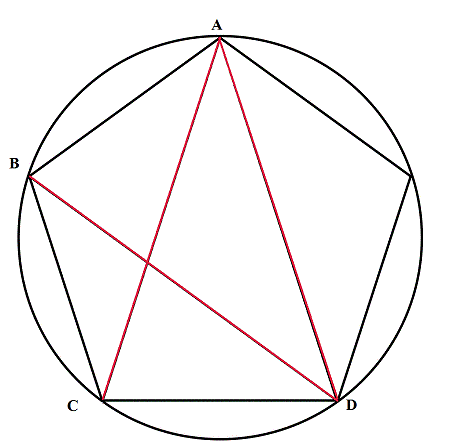
এই পঞ্চভুজটা একটা রেগুলার পেন্টাগন,যার পাঁচটা বাহুই সমান। একটা রেগুলার পেন্টাগনের কর্ণগুলোও সমান হয়,যেমনটা একটা বর্গের ক্ষেত্রে হয়,ঠিক তেমন।তাই AD,AC,BD ( লাল রঙে রঙিন) এরা সবাই সমান।
চতুর্ভুজ ABCD বৃত্তে অন্তর্লিখিত,তাই টলেমীর উপপাদ্য অনুসারে বলা যায়ঃ
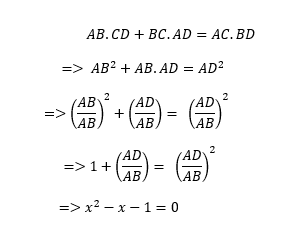
দ্বিতীয় লাইনে বাহু এবং কর্ণগুলো যে সমান,সেই শর্তটা ব্যবহার করেছি। আর এর পরের লাইনে AB^2 দিয়ে ভাগ করে দিয়েছি। আর শেষে এসে AD/AB কে x ধরে নিয়েছি।
তোমরা কি এই সমীকরণটিকে আগে কোথাও দেখেছো? এই সমীকরণের একটি সমাধান হচ্ছে (1+sqrt(5))/2 যাকে আমরা গোল্ডেন রেশিও বলে থাকি (গোল্ডেন রেশিও নিয়ে লিখা আছে আমাদের স্বশিক্ষার এই লিংকে )।
তার মানে,একটি রেগুলার পেন্টাগণের একটা কর্ণ আর একটা বাহুর অনুপাত গোল্ডেন রেশিও! প্রমাণ করলাম টলেমী দিয়ে। স্কুল কলেজের সেই বোরিং (!) টলেমীর উপপাদ্য দিয়ে। 😀
অফটপিকঃ চতুর্ভুজটি বৃত্তে অন্তর্লিখিত না হলে, অর্থাৎ যদি বৃত্তের কিছুটা বাহিরে চলে যায়,তখন টলেমীর অসমতা প্রয়োগ করে বাহু এবং কর্ণের মধ্যে সম্পর্ক নির্ণয় করা হয়। ব্যাপারটা এমনঃ

![]()
আজ এই পর্যন্তই! যেকোনো পরামর্শ / প্রশ্ন নির্দ্বিধায় জানানো যাবে।

