শিরোনাম দেখলেই বুঝে যাওয়ার কথা আমরা আজকে কোন জিনিসটা নিয়ে কথা বলবো। তবে আগে থেকেই বলে রাখি এখানে আমরা রসায়ন বইয়ের মতো গৎবাঁধা বুলি আওড়ে যাবো না। আমরা আজকে জিনিসটা আরেকটু ভালোভাবে বুঝার চেষ্টা করবো আর ফ্যারাডের সূত্র থেকে আসা সমীকরণকে একটু নেড়েচেড়ে দেখবো যা থেকে এক অসাধারণ সমীকরণ বেরিয়ে আসবে যেটা দিয়ে আমরা এ সম্পর্কিত যেকোনো গাণিতিক সমস্যাবলি খুব সহজেই সমাধান করতে পারবো।
আর দুই পর্বের এ লেখায় আজ আমরা কথা বলবো সে সূত্রের বেসিক নিয়ে। আর তারপরে আমরা এগুবো গাণিতিক কিছু সমস্যা নিয়ে। তো, শুরু করি!
ফ্যারাডের প্রথম সূত্রের বিবৃতিঃ তড়িৎ বিশ্লেষণের সময় যেকোনো তড়িৎদ্বারে সংগঠিত রাসায়নিক পরিবর্তনের পরিমাণ(ক্যাথোডে জমাকৃত ভর কিংবা অ্যানোডে ক্ষয়কৃত ভরের পরিমাণ) প্রবাহিত তড়িতের সমানুপাতিক।
কাজেই আমরা লিখতে পারি,
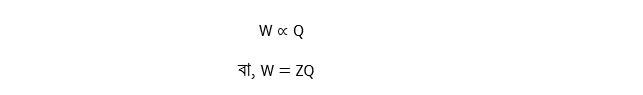
এতোদূর আসার পর আমরা Z কে সংজ্ঞায়িত করার কাজে লেগে পড়ি। এবার আমরা সংজ্ঞা দিই 1 Coulomb চার্জ অর্থাৎ 1 second সময়ে 1 amp বিদ্যুৎ প্রবাহিত হলে যতোটুকু পদার্থ জমা হয় তাকে বলা হয় Z.(ক্যানো আমরা নিজেরা এমন সংজ্ঞা দিই, ক্যানো-ই বা আমরা এভাবে সমীকরণের রাশিগুলোকে 1 দিয়ে সংজ্ঞায়িত করি সেসব আশা করি বোঝো। কাজেই আমি আর সেসব বোঝানোর দিকে না গেলাম!)। এখন খেয়াল করে দেখো, তুমি যখন কোনো তড়িৎবিশ্লেষ্য নিয়ে কাজ করবে তখন তার Z বের করা না থাকলে কিন্তু তুমি ঐ তড়িৎবিশ্লেষ্যের জমাকৃত ভর বের করতে পারো না। এখন ঝামেলা হলো, তুমি Z এর সংজ্ঞাই দিয়েছো 1 amp বিদ্যুৎ 1 second এ পরিবাহিত হলে যতোটুকু ভর জমা হয়। এখন যেকোনো তড়িৎবিশ্লেষ্যে জমাকৃত ভর বের করতে গিয়ে কিন্তু তোমাকে এক এর হিসাব করে আসতে হবে নতুবা তুমি Z এর মান সমীকরণে বসাতে পারো না।
কিন্তু সেটা কি কোনো ভালো কোনো বুদ্ধি হলো? সামান্য এক জমাকৃত ভর বের করতেই যদি এমন কষ্ট হয় তাহলে আর জীবনে কি থাকলো? 😛 কাজেই বিজ্ঞানীরা এক বুদ্ধি বের করলেন! বুদ্ধিটা অদ্ভূত রকমের সুন্দর। অ্যাভোগ্যাড্রোর সংখ্যা আর Mole Number নিয়ে তোমরা এ পর্যন্ত অনেক কথা শুনে এসেছো। এখানে এসে তুমি এর সৌন্দর্য উপলব্ধি করবে। ধরো, একটা সমীকরণঃ
![]()
এখন তুমি উপরের সমীকরণকে দুইভাবে Interpret করতে পারো।
১.তুমি বলতে পারো, একটা সিলভার আয়ন একটা ইলেক্ট্রন নিয়ে সিলভার ধাতুতে পরিণত হয়েছে
২. দুই নম্বরটা একটু মনোযোগ দিয়ে এবং ধৈর্যের সাথে দেখবে

এক নম্বর সূত্র থেকে আমরা পাই,

ঠিক উপরের সমীকরণ থেকে যেকোনো ধাতুর জন্যই আমরা Z এর মান জেনে ফেলতে পারি। আর পরে গাণিতিক সমস্যাবলিতে প্রবেশ করতে পারি। কিন্তু এতোটুকু আমরা সবাই জানি। কিন্তু যা জানি না সেটা হলো এ সমীকরণকে একটু নেড়ে-চেড়ে আমরা আরো অসাধারণ একটা সমীকরণ বের করে নিয়ে আসতে পারি। চলো সেটা বের করে ফেলিঃ
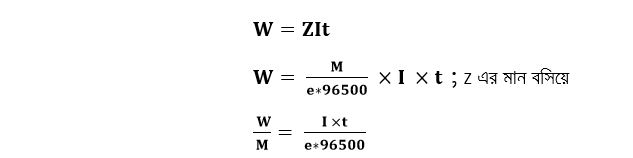
এতোটুকুতে এসে আমরা বামপক্ষের দিকে একটু মনোযোগ দিয়ে তাকাই। কি দেখা গেলো? W/M! অর্থাৎ এটা
মোল সংখ্যা বের করার সূত্র না?
কাজেই আমরা আরেকটু এগিয়ে লিখতে পারি নাঃ
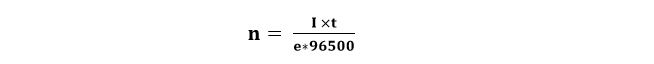
নিশ্চয়ই পারি। এখনই কিন্তু ঘটনা যা ঘটার ঘটে গেছে! আমরা Mole Number মোল সংখ্যা বের করার
একটা Chain Formula জানি কিনা! তারপরও আমি নিচেই লিখে দিচ্ছিঃ
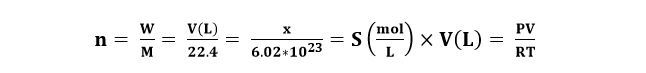
উপরের সমীকরণটা যারা জানো না তাদের জন্য বলছি, এই জগতে যতোভাবে Mole Number বের করা যায় তার সবটা একই সাথে দেয়া আছে উপরের Chain Formula তে। যেমন ধরো, তোমাকে দেয়া আছে একটা বস্তুতে কয়টা অণু আছে। এখন তোমাকে বললো , বস্তুটার কতো মোল তোমার কাছে আছে তাহলে কিন্তু তুমি Chain Formulaর x/6.02×10^23 সূত্রে বসিয়ে মান বের করে নিয়ে আসতে পারো। কিংবা তোমাকে বললো একটা দ্রবণের ঘনমাত্রা .05 mole/L. দ্রবণের আয়তন 2L. তাহলে ওই দ্রবণে কয়টি অণু আছে?।
তা কিন্তু তুমি Chain Formulaর একটা টুকরা কেটে নিয়ে x/6.02 x10^23 =S(mol/L)×V(L) এই সূত্র দিয়েই মানটা বের করে নিয়ে আসতে পারো। কাজেই বুঝতেই পারছো এই ফর্মুলাটা কতোটা জরুরি এবং কাজের জিনিস! কাজেই আমরা আমাদের কাঙ্ক্ষিত সূত্রটা পেয়ে গেলাম।
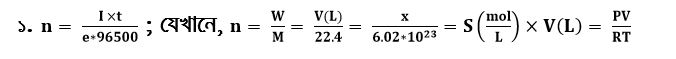
এখন থেকে আমরা এই সূত্র দিয়ে তড়িৎবিশ্লেষণের সব টাইপের গাণিতিক সমস্যা সমাধান করতে পারবো। আগামী পর্বে দেখা হচ্ছে, সেরকমই কিছু গাণিতিক সমস্যা নিয়ে। সে পর্যন্ত এতোটুকুই থাক!
পরিশিষ্ট১: অশেষ কৃতজ্ঞতা আমার গুরু মাহফুজুল হক ভাইয়ার কাছে। তার পিএইচডি গবেষণার মূল্যবান সময়ের কিছু এ লেখার জন্য দিয়েছেন এবং সর্বাত্মক উৎসাহ জুগিয়েছেন! এমনকি এই
সমীকরণটিও তার কাছ থেকেই শেখা!
পরিশিষ্ট২: তড়িৎ বিশ্লেষণের খুব বেসিক কিছু কথা-বার্তা আলোচনা করা হয়েছে স্বশিক্ষারই একটা লেখায়। জানতে চাইলে ক্লিক করো এখানে!

প্রথমবারের মত চ্যাপটারটি যারা ধরবে, তাদের জন্য উপকারী পোস্ট
ধন্যবাদ 🙂