টারনারি সার্চ

টার্নারী সার্চ মূলত একটি সার্চিং টেকনিক । আমরা আগে বাইনারী সার্চ দেখেছি । যেটা মূলত আমাদের পুরো সার্চিং স্পেশ করে অর্ধেক অর্ধেক করে আমাদের প্রবলেম এর সমাধান করে ।

বাইনারী সার্চ যেমন আমাদের পুরো স্পেস কে ২ ভাগ করে । টার্নারী সার্চ প্রতি স্টেপ এ আমাদের সার্চিং স্পেস ( যেই স্পেসে আমাদের সমাধান আছে) কে তিন ভাগ করে ফেলে । তারপর সেই তিন ভাগ থেকে আমাদের সলিউশন বের করবে । এখন প্রশ্ন, বাইনারী সার্চ আর টার্নারী সার্চ কোনটা বেটার বা কোনটার কি কাজ ?

আগে বলি, বাইনারী সার্চ কেন আর কোথায় কাজ করে । বাইনারী সার্চ মূলত যেখানে ইনক্রিজিং আর ডিক্রিজিং সিকুয়েন্স আছে সেই ক্ষেত্রে কাজ করে । একটা উদাহরণ দেই । মনে করি আমি একটা ননলিনিয়ার ইকুয়েশন সলভ করছি । আমরা চাচ্ছি,

y = x^3 – x + 1  এই সমীকরণের এমন x এর মান বের করতে যাতে সেই x এর মানের জন্য y এর মান শূন্য হয়ে যায় । এখন এই সমীকরণে x এর তিনটি  মান আছে যার জন্য সমীকরণটা সিদ্ধ হবে । এই সমীকরণ এর সমাধান তিনটি কারন এখানে x এর পাওয়ার তিন । এখন আমরা একটা নির্দিষ্ট x এর মানের রেঞ্জ দিয়ে দিব আর বলব,এই রেঞ্জে x এর কোন মানের জন্য  সমীকরণ এর মান বা y এর মান শূন্য হয় ।

আমরা এখন গ্রাফটি দেখি ।

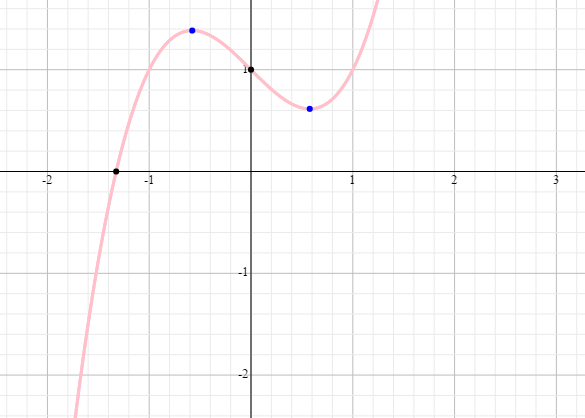
এখন, যদি বলি [-২,১] এই রেঞ্জ এর মধ্যে আমাকে এমন একটা x এর মান বের করে দিতে যার জন্য এই সমীকরণটির মান শূন্য হয় । তাহলে আমরা কীভাবে এই সমস্যাটার সমাধান করতে পারি বাইনারী সার্চ দিয়ে ।

আমরা কি করব, আমরা প্রথমে (-২+১)/২ = -০.৫ এই মানটির জন্য সমীকরণের মান দেখব, সেটা এখানে হবে ১.৩৭৫ । আচ্ছা । এখন আমরা একটা জিনিস একটু চিন্তা করি যেই পয়েন্ট এ বা যেই x এর মানের জন্য একটা সমীকরণের মান শুন্য হয় , আমরা বলতে পারি গ্রাফটা x অক্ষকে ঐ বিন্দুতে ছেদ করে । আর যেই বিন্দুতে এক্স অক্ষকে ছেদ করে সেই বিন্দুতে অবশ্যই y এর মান শুন্য আর এটাই তো মূলত সমীকরণের সমাধান, তাই না ? । তাহলে একটা জিনিস আমাদের দরকার, এমন সব পয়েন্ট গুলো নিয়ে (বা x নিয়ে)কাজ করা যার একটার জন্য y এর মান > ০ এবং আরেকটার জন্য y <0 । কেন করা ? কারণ যেহেতু এই দুই x এর জন্য একবার y>0 এবং আরেকবার y<0 অবশ্যই এর মধ্যে এমন একটা মান আছে বা x আছে  যার জন্য y = 0, এই দুইটা x এর ভ্যালুর জন্য y>0 এবং y<0 এর অর্থ হল গ্রাফটা এই দুইটা x এর মানের মধ্যে অবশ্যই x axis কে ক্রস করে , আর তা নাহলে কখনোই y>0 এবং y <0 পাওয়া যেত না ।

আমাদের বাইনারী সার্চ মূলত এই রিডিউস এর কাজ টাই করে । যেমন আমাদের উপরের মান x = -০.৫, এটাতে y এর মান ১.৩৭৫ । এখন দেখি আমরা যদি এর পরে x = -2 এবং x = -0.5 নিয়ে কাজ করি তাহলে আমরা  দেখব প্রথমটাতে y>0 এবং দ্বিতীয়টাতে y<0 ,এর মানে এই সিকুয়েন্সে একবার হলে আমদের সমীকরণ x এক্সিস কে ছেদ করে । তাহলে অবশ্যই আমরা আমাদের সার্চ স্পেস রিডিউস করতে পারি । কিন্তু x= -0.5 এবং x= 1 পেলে আমরা দুইটা সেম সাইন এর y এর মান পেতাম এর অর্থ হল এই স্পেসে আমাদের সমীকরণ এক্স এক্সিস কে ছেদ করে না । তাহলে অবশ্যই আমরা একে নিব না । এরপরে দেখব, আমার x = -2 এবং x = -0.5  থেকে প্রাপ্ত এর মিড x = -1.25 , এখন আমরা দেখব আমরা যদি x = -2 এবং x = -1.25 নিয়ে কাজ করি তাহলে বেটার কারণ তুলনামূলক ভাবে ছোট স্পেসে আমরা জানি সমীকরণ x এক্সিস কে ক্রস করে ।

তাহলে আমরা এভাবে করে আস্তে আস্তে সমাধানের কাছে আসতে থাকব আর একপর্যায়ে দেখতে থাকব, y এর মান শূন্যের কাছাকাছি চলে আসছে, মানে আমরা আমাদের সমাধান x এর কাছে পৌছাতে যাচ্ছি । এখন আমাদের সার্চিং এর উপর ডিপেন্ড করে আমাদের সমাধানের অ্যাকুরেসি ডিপেন্ড করবে । কারন যেহেতু এই সমীকরণের কোন সসীম সমাধান নেই । আমরা যত সার্চ করব তত বেশি আমাদের টার্গেট ভ্যালুর কাছে পৌছাতে থাকব ।

তো এইটাই হল বাইনারী সার্চের কাজ করার উপায় । এখন প্রশ্ন হল, এইটার মূল থিম কি । আমরা সবসময় কোন সিকুয়েন্স নিয়ে কাজ করছি ?

আমরা সবসময় এমন একটা রেঞ্জ নিয়ে কাজ করছি যেই রেঞ্জে আমাদের একটা ইনক্রিজিং আর ডিক্রিজিং সিকুয়েন্স আছে(অপোজিট ভাবে একটা পয়েন্ট এর জন্য ইনক্রিজিং আরেকটা পয়েন্ট এর জন্য ডিক্রিজিং) । যা থেকে আমরা বলতে পারি আমাদের টার্গেট সলিউশন এই রেঞ্জ এর মধ্যেই আছে, এর বাইরে আর কোন কিছু নিয়ে কাজ করা দরকার নেই । এভাবে আমরা আমাদের স্পেস রিডিউস করে সলিউশনের কাছে পৌছাই । যেখানে কোন ইঙ্ক্রিজিং বা ডিক্রিজিং সিকুয়েন্স নাই বা যেখানে আমরা এই ইনক্রিজিং ডিক্রিজিং সিকুয়েন্স থাকা সত্ত্বেও আমরা বলতে পারি না আমাদের সার্চিং স্পেস রিডিউস হয়েছে সেখানে আমাদের বাইনারী সার্চ কাজ করে না । এই সব ক্ষেত্রেই আমাদের লাগে টার্নারী সার্চ ।

মুলত, বাইনারী সার্চ যেখানে একটা মিড ভ্যালু/ আমাদের রেঞ্জের মধ্যে মাঝের কোন একটা ভ্যালু দিয়ে একটা ডিসিশন দিতে পারে । টার্নারী সার্চ সেখানে  মাঝের দুইটা ভ্যালু এর ওপর বেস করে ডিসিশন নিবে । মানের আমাদের এখানে মিড হবে দুইটি । যেমন ধর আমাকে বলা হল, উপরে যেই ফাংশনটা লিখেছি সেটার x এর  কোন মানের জন্য (একটা নির্দিষ্ট রেঞ্জে) একটা ম্যাক্সিমা বা মিনিমা বের করতে । বা কোন রেঞ্জ এ এই ফাংশটার সর্বোচ্চ অথবা সর্বনিম্ন মান বের করতে ।

আমরা খুব সহজে ক্যালকুলাসের সাহায্যে ডিফরেনশিয়েট করে এই ভ্যালুগুলো বার করতে পারি । কিন্তু প্রশ্ন হল এখানে বাইনারী সার্চ কাজ করবে কিনা । যদি করে থাকে তাহলে কেন করবে আর যদি না করে থাকে তাহলে কেন করবে না ।

এখন দেখি আমরা বাইনারী সার্চ এ সবসময় পুরো রেঞ্জ এর মাঝের কোন একটা ভ্যালু বার করি । এরপরে সেখান ইনক্রিজিং বা ডিক্রিজিং সিকুয়েন্স এর ওপর বেস করে কাজ  করি । এখন কি আমরা একটা ভ্যালু দিয়ে ডিটাইরমাইন করতে পারি ? উপরের উদাহরণ দেখি, এখানে আমরা বললাম [-১,১] এই রেঞ্জে ফাংশনের ম্যাক্সিমা বার করতে ।  এখন আমি এদের মিড বার করলাম ০, এতে y এর মান ১ আর x = -১ এ y = ১, এক্স = 1 এ y = 1 এখন এখান থেকে আমি কোনভাবে ডাইরেক্টলি বলতে পারি এদের মাঝে কোন পিক(Maximum Pick, Minimum pick) আছে কিনা ? বলতে পারি না, কারণ একটা পয়েন্ট থেকে আমি জাস্ট বলতে পারি আমাদের কার্ভটা কোনদিকে মুভ করে, কিন্তু কোন গ্রাফের কোন পিক বোঝা সম্ভব না । কারণ পিকের অংশগুলোতে আমরা যদি খেয়াল করি, পিক পয়েন্ট এর একপাশে গ্রাফ ওই পয়েন্ট এর দিকে আসছে আরেকটা পাশে গ্রাফ টা ঐটা থেকে দূরে সরে যাচ্ছে । তাই আমি বাইনারী সার্চ করলে যে কোন একটা পাশের ডিসিশন নিতে পারি যে সেটা আল্টিমেটলি নিচে মুভ করে অথবা উপরে মুভ করে(ইনক্রিজিং/ডিক্রিজিং) । কিন্তু আমি কোনদিন বলতে পারব না যে আলটিমেটলি পুরো গ্রাফটার এই রেঞ্জে আদৌ কোন পিক পয়েন্ট আছে কিনা , কারণ পিক পয়েন্ট এর একপাশে ইনক্রিজিং আর আরেকপাশে ডিক্রিজিং সিকুয়েন্স থাকে । তাই শুধু একটা কিছু দিয়ে আমরা ডিসিশনে পৌছাতে পারব না । তাই আমরা এখন ২ টা মিড বার করব ।

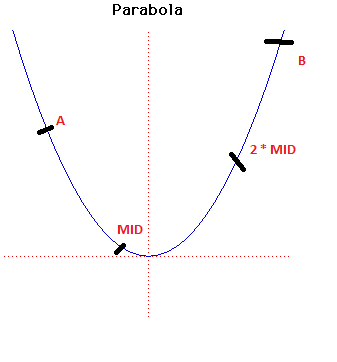
আচ্ছা, আমি যদি এখন একটা মিড না নিয়ে ২ টা মিড নেই, দ্বিতীয় মিড (২*মিড = mid2) তাহলে আমি ফাংশনের ২ টা ভ্যালু বার করলাম । এখন আমি দেখব ২ টা ভ্যালুর জন্য মান কেমন হয় । যদি দেখি f(mid1) < f(mid2) [ উপরের চিত্রের মত, উপরের চিত্রটা একটা আরবিটারি ফাংশনের গ্রাফ আমরা এখন,  x এর কোন মানের জন্য ফাংশনের মান মিনিমাম হয় সেটা বার করতে চাচ্ছি]  তাহলে আমরা কি বলতে পারি, আমরা বলতে পারি যেহেতু mid2 তে যেহেতু ফাংশনের ভ্যালু, mid1 এ ফাংশনের ভ্যালু থেকে বাড়ছে তাই আমি অবশ্যই বলতে পারি মিড২ থেকে ছোট কোন x এর ভ্যালুর জন্য  আমি অবশ্যই ফাংশনের মিনিমাম কোন ভ্যালু পেতে পারি , তাহলে আমার স্পেস রিডিউস করতে পারি আর নতুন সার্চিং রেঞ্জ করতে পারি [A,mid2]  , এভাবে করে আমি আমার পুরো সার্চিং স্পেস করে ৩ টা ভাগ করে দেখি মাঝের ২ টা পয়েন্ট নিয়ে দেখি একটা সাপেক্ষে আরেকটার চেঞ্জ কীরকম । যদি আমি যেকোন একটা পয়েন্ট কনসিডার করতাম তাহলে পিকের যে কোন এক পাশের মুভকে সিমুলেট করতে পারতাম, কিন্তু যেহেতু আমাদের পিক দরকার তাই আমি ২ টা সাইডের ভ্যালু বার করি আর তারপরে ডিসিশন দেই এই দুইটা  ভ্যালুর মাঝে পিক থাকা পসিবল কিনা, একপাশে ইনক্রিজিং আর আরেকপাশে ডিক্রিজিং সিকুয়েন্স আছে কিনা তা দেখে । এভাবে করেই আমাদের টার্নারী সার্চ কাজ করে ।

আশা করি ইমপ্লিমেন্টেশনে প্রবলেম হবে না ।

মূল থিম,  আমি মাঝের দুইটা পয়েন্ট এ ফাংশনের ভ্যালু বার করব । এরপরে আমি দেখব একটা সাপেক্ষে আরেকটার চেঞ্জ কীরকম । অবশ্যই একটা নিম্নমুখী আরেকটা ঊর্ধমুখী হবে (যদি সলিউশন থাকে) তাহলে আমি যদি চাই কম ভ্যালু নিয়ে কাজ করব তাহলে হাই কে রিডিউস করব আর তানা হলে লো কে রিডিউস  করব ।

কিছু সলভ করার জন্য প্রবলেমঃ

CLOSEST DISTANCE, Point Segment Distance (3D)

প্রবলেমগুলো ট্রাই করব । আর না পারলে আমি ২য় প্রবলেমটার সলিউশন দিচ্ছি, এটা দেখে নিতে পারো । এটা দেখলে হয়তো ইমপ্লিমেন্টেশন আইডিয়া ক্লিয়ার হবে ।

সলিউশনঃ https://ideone.com/k9L0TL

কৃতজ্ঞতা স্বীকারঃ

হাসনাইন হেইকেল ।

জাহিদুল হাসান ।