তোমরা সবাই হয়ত গাউস এর নাম শুনেছো। গাউস পৃথিবীর নামকরা গণিতবিদদের মধ্যে একজন কিন্তু গণিতবিদ হলেও তার পদার্থবিজ্ঞানেও বেশকিছু অবদান আছে। সেই অন্যতম একটি অবদান হল তার দেয়া স্থির তড়িৎ ও চুম্বকত্ব সম্পর্কিত Law.
আমরা আজ সেটি নিয়ে অল্পবিস্তর আলোচনা করে তা সম্পর্কিত গাণিতিক সমস্যা নিয়ে আলোচনা করব।
তাহলে আর দেরি না করে শুরু করে ফেলা যাক। 😀
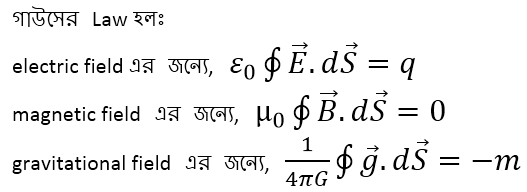
অনেকেই হয়ত চোখ বড় বড় করে তাকিয়ে আছো এ কি বিদঘুটে Law রে বাবা। :O চোখ বড় করার কিছুই নেই, বিষয়টাকে পরিষ্কার করার জন্যেই আমাদের এ আলোচনা। 😀
(আমরা প্রকৃতপক্ষে তড়িৎ ক্ষেত্র নিয়েই বেশিরভাগ আলোচনা করব, চৌম্বক ও মহাকর্ষীয় ক্ষেত্র নিয়ে সামান্য আলোচনা থাকবে।)
গাউসের Law তে বিস্তারিত প্রবেশের আগে আমাদের Law সম্পর্কিত বেশ কিছু কথা জেনে নেয়া দরকার।
(উপরের লিখা সমীকরণগুলো কেউ যদি দেখে থাক তাহলে আপাতত ভুলে যাও, আর কেউ যদি না দেখে থাকো তাহলে আর দেখার দরকার নেই এখন। :D)
গাউসের Law হল vector field আর source এর মধ্যে একটি সম্পর্ক। কি বুঝলে না? হয়ত ভাবছো vector field , source এগুলো কি জিনিস, এলই বা কোত্থেকে? :/
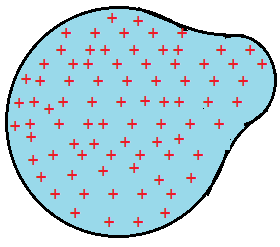
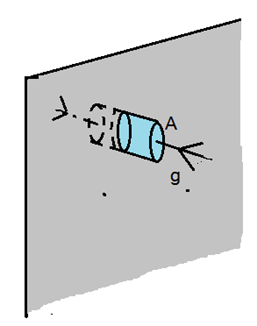
ধরো, তোমার কাছে একটা তীর নিক্ষেপকারী যন্ত্র আছে যেটাতে তীর ভরে দিলে তা মেশিনগানের মত নিয়মিত তীর ছুড়তে পারে আর চারদিকে তীর ছুড়তে পারে। তুমি যন্ত্রটিতে তীর ভরে দিয়ে সেটিকে একটি সরু ওয়াচ টাওয়ার এর নিচে রেখে দিয়ে দৌড়ে ওয়াচ টাওয়ার এর উপরে উঠে গেলে এবং তীর ছোড়া শুরু হওয়ার কিছুক্ষণ পর উপর থেকে একটা ছবি তুলে ফেললে। বলো তো, তুমি ঠিক নিচের ডানের ছবিটার মত দেখতে পাবে কিনা?
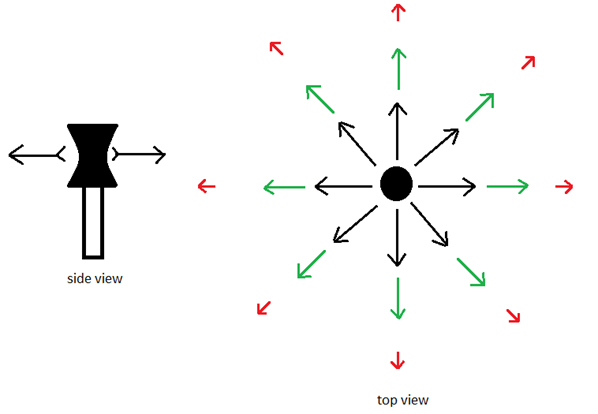
তাই তো দেখতে পাওয়ার কথা কারণ যেই তীরগুলো তোমার কাছে সেগুলো তুমি বড় দেখবে আর যেগুলো দূরে সেগুলো তুমি ছোট দেখবে বা অন্য কথায় বলা যায় যেগুলোর বেগ বেশি সেগুলো তুমি বড় দেখবে আর যেগুলোর বেগ কম সেগুলো তুমি ছোট দেখবে (কারণ কাছেরগুলোর বেগ বেশি দূরেরগুলোর বেগ কম)। তার মানে তোমার তোলা ছবিটিতে প্রতিটি তীর একটি করে বেগের মান ও দিক নির্দেশ করছে।
তাহলে আমরা বলতে পারি, যে জায়গাজুড়ে তীরগুলো ছড়িয়ে পড়েছে তা হল vector field আর তীর মারার যন্ত্রটি হল source । তার মানে সহজ কথায় আমরা যদি কোনো একটা জায়গার প্রতিটি বিন্দু একটি করে vector assign করতে পারি বা প্রতিটি বিন্দুতে একটি করে vector পাই তাহলে সে জায়গাটা হল vector field.
অন্য কথায় বলা যায়, গাউসের Law কোনো একটা field এর flux এর সাথে ঐ field এর source এর সম্পর্ক প্রকাশ করে।
এখন আমাদের প্রথমে যেই শব্দটির সাথে পরিচিত হওয়া দরকার তা হল flux. (আমরা বেশিরভাগ ক্ষেত্রে তড়িৎক্ষেত্র ব্যবহার করে বললেও ব্যপারটা সবগুলো field এর ক্ষেত্রেই সত্য।)
vector field আর তার source এর মধ্যে সম্পর্ক সহজভাবে বুঝানোর জন্যে আমরা flux রাশিটি ব্যবহার করি। কোনো একটা field এর flux পরিমাপ করা হয় যতগুলো কাল্পনিক রেখা কোনো hypothetical surface (যা closed বা open উভয় রকমই হতে পারে) কে ছেদ করে বা তার ভিতর দিয়ে অতিক্রম করে তাদের সংখ্যা দ্বারা।
এই কাল্পনিক রেখাগুলোকে বলা হয় flux lines.
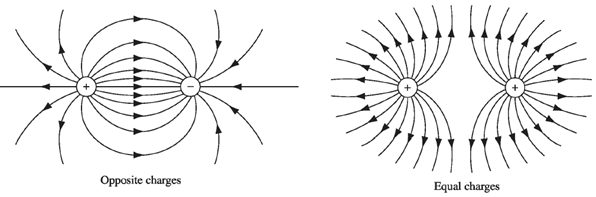
ধনাত্মক চার্জ থেকে flux lines বের হয় আর ঋণাত্মক চার্জে flux lines প্রবেশ করে। flux line গুলো পরস্পরকে বিকর্ষণ করে, তাই এরা কখনো পরস্পরকে ছেদ করে না।
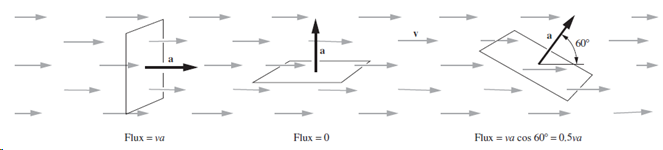
এখন একটি তল যদি ছবির মত খাড়াভাবে থাকে তাহলে তার মধ্যে দিয়ে সর্বাধিক flux পাওয়া যাবে। আর যদি নোয়ানো থাকে তাহলে তার মধ্যে দিয়ে সর্বনিম্ন flux পাওয়া যাবে। আর যদি তৃতীয় অবস্থার মত হেলানো থাকে তাহলে তার মধ্যে দিয়ে ঠিক ততটুকুই flux পাওয়া যাবে যতটুকু ঐ তলটির একটি অংশ যদি খাড়াভাবে থাকতো তাহলে যত পাওয়া যেত তত। এখন যদি তলের ক্ষেত্রফল a হয় তাহলে খাড়া অবস্থায় পুরো a এর মধ্যে দিয়েই তড়িৎক্ষেত্র প্রবাহিত হবে, যদি নোয়ানো থাকে তাহলে তলের মধ্যে দিয়ে কোনো তড়িৎক্ষেত্রই প্রবাহিত হবে না, হেলানো অবস্থায় পুরো তলের cosθ পরিমাণ অংশের মধ্যে দিয়ে তড়িৎক্ষেত্র প্রবাহিত হবে। এখন যদি প্রশ্ন করা হয় তলটির মধ্যে দিয়ে কি পরিমাণ field প্রবাহিত হচ্ছে? তাহলে উত্তর হবে: প্রবাহ × ক্ষেত্রফল আর এ পরিমাণটাই হল flux।
অর্থাৎ, flux = field . area বা ![]()
তার মানে flux এর অর্থ দাঁড়াচ্ছে কোনো একটি field এর মধ্যে যদি একটি তল ডুবানো থাকে তাহলে তার কোনো অংশ ঐ field এ লম্বভাবে ডুবানো থাকলে তার মধ্যে দিয়ে যে পরিমাণ field প্রবাহিত হত তাই অর্থাৎ কোনো একটি field এ লম্বভাবে ডুবানো তলের মধ্যে দিয়ে প্রবাহিত field এর পরিমাণই হল flux।
এরপর যে জিনিসটি সম্পর্কে জানবো তা হল ভেদনযোগ্যতা (permittivity)। সহজ কথায় ভেদনযোগ্যতা হল কোনো একটি মাধ্যমের মধ্যে দিয়ে একটি field তৈরি হতে যে পরিমাণ বাধার সম্মুখীন হতে হয় বা যে পরিমাণ বাধা পায় তাই।অর্থাৎ মাধ্যমের যে বৈশিষ্ট্যের জন্যে তার মধ্যে দিয়ে flux line গুলো ছড়িয়ে পড়তে বাধা পায় তাই হল ঐ মাধ্যমের ভেদনযোগ্যতা।
এবার তাহলে উপরের গাউসের Law গুলো দেখতে পারো।
গাউসের law থেকে কুলম্বের law প্রতিপাদন:
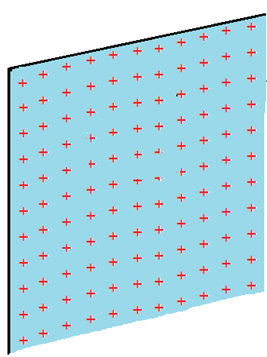
ছবি থেকে দেখা যাচ্ছে, E এবং ds উভয়েই ব্যাসার্ধ বরাবর বাইরের দিকে কাজ করছে। তাদের মধ্যকার অন্তর্ভুক্ত কোণ তাই 0o । আর এজন্যে
 যা কুলম্বের law নামে পরিচিত।
যা কুলম্বের law নামে পরিচিত।
গাউসের law এর ছোট্ট প্রমাণঃ
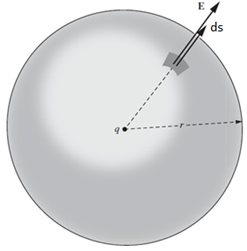
একটি q C এর বাইরে চারদিকে r ব্যাসার্ধের একটি আবদ্ধ গোলকের তল বা পৃষ্ঠ (surface) চিন্তা করি। তাহলে আমরা জানি, গোলকের পৃষ্ঠে তড়িৎক্ষেত্র, E এর মান হবে ![]() আর দিক হবে ব্যাসার্ধ বরাবর বাইরের দিকে। গোলকের পৃষ্ঠের ক্ষেত্রফল
আর দিক হবে ব্যাসার্ধ বরাবর বাইরের দিকে। গোলকের পৃষ্ঠের ক্ষেত্রফল ![]() তাহলে গোলকের পৃষ্ঠ দিয়ে নির্গত flux, Φ এর পরিমাণ হবে
তাহলে গোলকের পৃষ্ঠ দিয়ে নির্গত flux, Φ এর পরিমাণ হবে
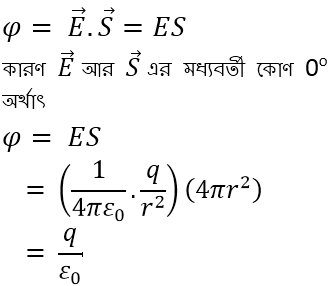
যেকোনো আকারের গোলকের জন্যেই এটা খাটে তার মানে flux এর মান গোলকের আকারের উপর নির্ভর করে না।
(কুলম্বের Law তে কেন 4π এই factor টা নেয়া হয়েছে তার একটা গুরুত্ব হয়ত এতক্ষণে বুঝতে পেরেছো। 😀 )
এখন আমরা কেবল দেখাবো যে শুধু গোলকীয় তলই নয় যেকোনো আকৃতির তলের জন্যেই এটা খাটে।
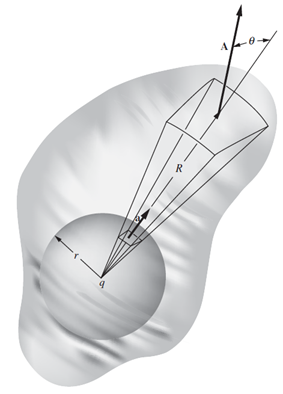
উপরের ছবিতে আমরা যেকোন আকৃতির (ধরলাম ওলকচু আকৃতির) একটা তল ধরে নিয়েছি যা গোলকীয় তলটিকে আবদ্ধ করে আছে। তার মানে আমরা শুধু এইটুকু দেখাতে চাইছি যে, গোলকের মধ্যে দিয়ে যে flux নির্গত হবে ওলকচু আকৃতির তলটির মধ্যে দিয়েও সেই একই পরিমাণ flux নির্গত হবে।
এবার ছবির কোণকটির দিকে দেখ তা q থেকে নির্গত হয়ে গোলকটি থেকে,

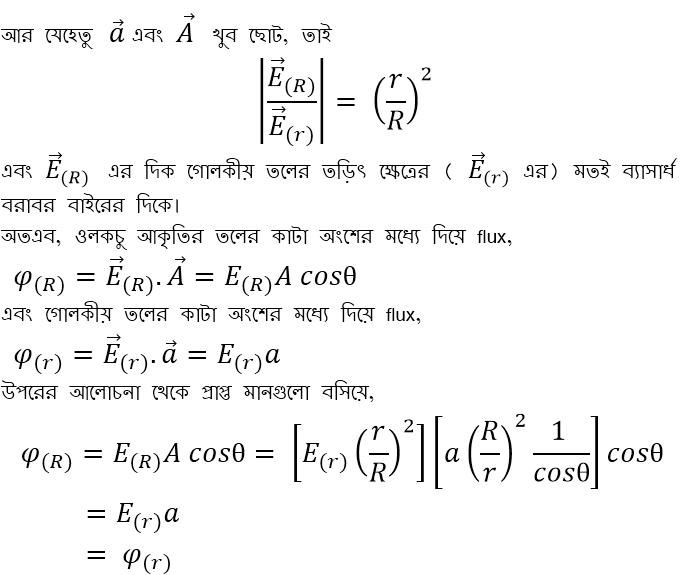
এখন ওলকচু আকৃতির তলটির সমগ্র পৃষ্ঠকে একইভাবে ছোট ছোট টুকরায় ভাগ করে গোলকীয় তলের সমগ্র পৃষ্ঠের ছোট ছোট টুকরার সাথে এক এক করে মিল করা যায়। তাই বলা যায়, দুই ধরণের তলের মধ্যে দিয়েই মোট flux এর পরিমাণ সমান হবে। তাহলে ওলকচু আকৃতির তলের মধ্যে দিয়ে flux, ![]() ।এখন যেহেতু ওলকচু আকৃতির তলটি আমরা ইচ্ছামত বেছে নিয়েছি, তাই আমরা বলতে পারি, যেকোনো আকার বা আকৃতির আবদ্ধ তলের মধ্যে দিয়ে flux এর পরিমাণ হবে
।এখন যেহেতু ওলকচু আকৃতির তলটি আমরা ইচ্ছামত বেছে নিয়েছি, তাই আমরা বলতে পারি, যেকোনো আকার বা আকৃতির আবদ্ধ তলের মধ্যে দিয়ে flux এর পরিমাণ হবে ![]() । অর্থাৎ প্রমাণ হয়ে গেলো গাউসের Law,
। অর্থাৎ প্রমাণ হয়ে গেলো গাউসের Law,
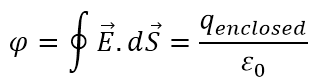
তার অর্থ কোনো আবদ্ধ তলের মধ্যে দিয়ে flux এর মান তলের আকার বা আকৃতির উপর নির্ভর করে না, তা কেবল চার্জের পরিমাণের উপর নির্ভর করে। চার্জ ধনাত্মক হলে flux এর মান ধনাত্মক অর্থাৎ flux line গুলো তল থেকে বের হয়ে যাবে, চার্জ ঋণাত্মক হলে flux এর মান ঋণাত্মক অর্থাৎ flux line গুলো তলের ভিতরে প্রবেশ করবে। আর চার্জ যদি আবদ্ধ তলের বাইরে থাকে তাহলে তলের মধ্যে দিয়ে flux এর মান হবে শূন্য (zero)।
এই ফলাফল আমাদের ধারণার সাথে সামঞ্জস্যপূর্ণ কারণ আমরা যদি আবার সেই প্রথমে দেখা তীর নিক্ষেপকারী আমাদের যন্ত্রটার দিকে দেখি তাহলেই বুঝতে পারব কোনো একটি তলের মধ্যে দিয়ে নির্গত তীরের সংখ্যা আসলে তলের আকার বা আকৃতির উপর নির্ভর করে না, নির্ভর করে কি হারে তীর ছোড়া হচ্ছে আর কি হারে তীর তলের মধ্যে দিয়ে যেতে পারছে (মানে ভেদনযোগ্যতা) তার উপর।

আমরা গাউসের Law সম্পর্কিত সমস্যা সমাধানের সময় প্রতিসমতা রক্ষা করে সুবিধাজনক কিছু Gaussian surface কল্পনা করে নিব। Gaussian surface হিসেবে তিন ধরণের প্রতিসমতা ব্যাবহার করবঃ
১) গোলকীয় প্রতিসমতাঃ একটি সমকেন্দ্রিক গোলক ভেবে নিয়ে।
২) সিলিন্ডার প্রতিসমতাঃ একটি সমকেন্দ্রিক সিলিন্ডার ভেবে নিয়ে।
৩) তল প্রতিসমতাঃ একটি Gaussian pillbox ভেবে নিয়ে।
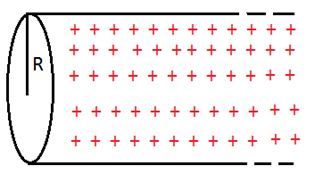
সমস্যা- ১: সুষম তড়িৎক্ষেত্রে hypothetical সিলিণ্ডার
একটি hypothetical সিলিণ্ডার এর ভূমির ব্যাসার্ধ r এবং এটি এর অক্ষের সমান্তরালে একটি E মানের সুষম তড়িৎক্ষেত্রের মধ্যে অবস্থিত। এর মধ্যে দিয়ে flux নির্ণয় কর।
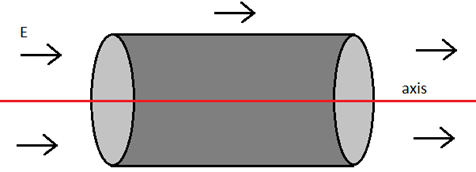
সমাধান:
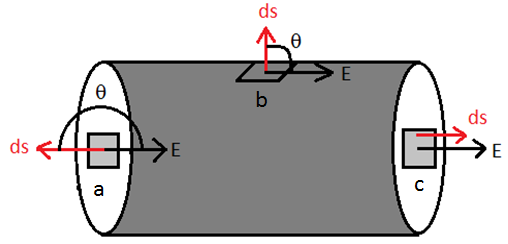
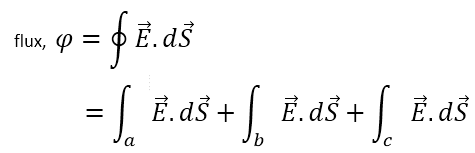
a এর জন্যে কোণ θ = 1800 , E এর মান সবজায়গায় ধ্রুবক। ds এর দিক E এর ঠিক বিপরীত।
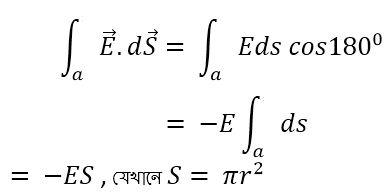
এটা সিলিণ্ডারের বৃত্তীয় তলের সব a এর জন্যে সত্য।
c এর জন্যে কোণ θ = 00 , E এর মান সবজায়গায় ধ্রুবক। ds এর দিক E এর দিকে।
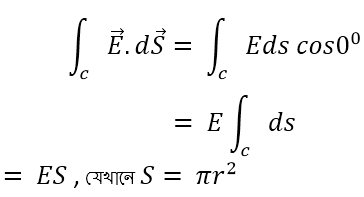
এটা সিলিণ্ডারের বৃত্তীয় তলের সব c এর জন্যে সত্য।
b এর জন্যে কোণ θ = 900 , E এর মান সবজায়গায় ধ্রুবক। ds এর দিক E এর দিকের সাথে লম্ব।
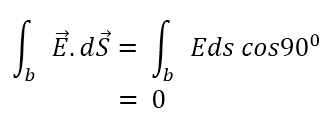
এটা সিলিণ্ডারের বক্র তলের সব b এর জন্যে সত্য।
অর্থাৎ
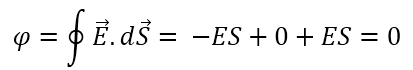
একটি hypothetical সিলিণ্ডার এর ভূমির ব্যাসার্ধ r এবং এটি এর অক্ষের সমান্তরালে একটি E মানের সুষম তড়িৎক্ষেত্রের মধ্যে অবস্থিত থাকলে এর মধ্যে দিয়ে flux = 0
এই ব্যাপারটা আমরা গাউসের Law দিয়ে খুব সহজেই প্রমাণ করে ফেলতে পারি।
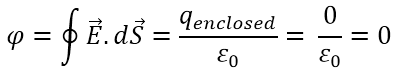
কি হয়ে গেলো না? 😀
সমস্যা- ২: আবারও সুষম তড়িৎক্ষেত্রে hypothetical সিলিণ্ডার
একটি hypothetical সিলিণ্ডার এর ভূমির ব্যাসার্ধ r এবং এটি এর অক্ষের সাথে লম্বভাবে একটি E মানের সুষম তড়িৎক্ষেত্রের মধ্যে অবস্থিত। এর মধ্যে দিয়ে flux নির্ণয় কর।
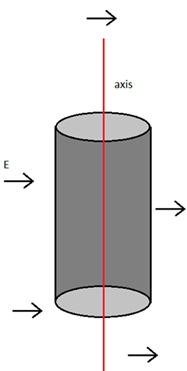
সমাধান:
তোমরা আগের মত করে, করে ফেলার চেষ্টা করো আমি ততক্ষণে গাউসের Law দিয়ে প্রমাণটা সেরে ফেলি।
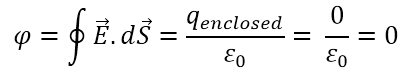
একটি hypothetical সিলিণ্ডার এর ভূমির ব্যাসার্ধ r এবং এটি এর অক্ষের সাথে লম্বভাবে একটি E মানের সুষম তড়িৎক্ষেত্রের মধ্যে অবস্থিত থাকলে এর মধ্যে দিয়ে flux = 0
(আচ্ছা বল দেখি আগেরটার সাথে পার্থক্য কোথায় হবে? শুধু পার্থক্য হবে θ এর মানে আগে বক্রতলে ছিল θ = 900 আর বৃত্তীয় তলে একপাশে ছিল θ = 00 আর অপরপাশে θ = 1800 আর এবার বৃত্তীয় তলে হবে θ = 900 আর বক্রতলের একপাশে যেকোনো একটা ছোট surface এর বিপরীতে অপর একটি surface থাকবে যার flux হবে ঠিক আগের ছোট surface এর বিপরীত চিহ্নবিশিষ্ট কিন্তু সমান মানের।)
সমস্যা- ৩: একটি চার্জিত গোলক
একটি ব্যাসার্ধের গোলকের চার্জ ঘনত্ব ρ যা সমভাবে সমগ্র তলজুড়ে বিস্তৃত। কেন্দ্র থেকে r m দূরে কোনো একটি বিন্দুতে তড়িৎক্ষেত্র E এর মান কত?
(i) যখন r < R (ii) যখন r > R
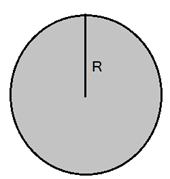
সমাধান:
গাউসের Law অনুসারে,
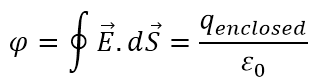
যেহেতু চার্জ সুষমভাবে বণ্টিত আছে তাই, ![]() এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর বাইরের দিকে ক্রিয়া করছে। Gaussian surface হিসেবে আমরা একটা r ব্যাসার্ধ এর গোলক কল্পনা করব।
এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর বাইরের দিকে ক্রিয়া করছে। Gaussian surface হিসেবে আমরা একটা r ব্যাসার্ধ এর গোলক কল্পনা করব।
(i) যখন r < R
যেহেতু ভিতরের নীল গোলকের বাইরের চার্জগুলোর তড়িৎক্ষেত্রে কোনো প্রভাব নেই তাই surface এর ক্ষেত্রফল হবে ![]() অর্থাৎ,
অর্থাৎ,

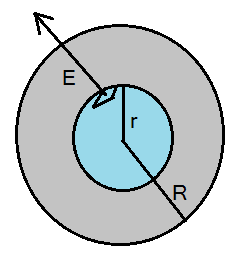
(ii) যখন r > R
যেহেতু নীল গোলকের ভিতরের চার্জগুলোর জন্যে তড়িৎক্ষেত্র তৈরি হবে তাই surface এর ক্ষেত্রফল হবে ![]() আর চার্জের পরিমাণ হবে কালো গোলকের আয়তনের সমানুপাতিক অর্থাৎ,
আর চার্জের পরিমাণ হবে কালো গোলকের আয়তনের সমানুপাতিক অর্থাৎ,

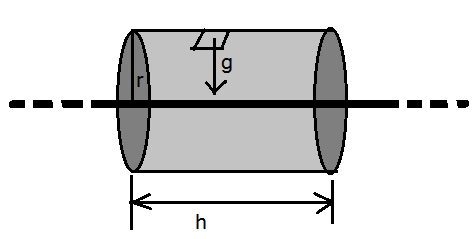
সমস্যা- ৪: অসীম দৈর্ঘ্য এর চার্জিত রেখা
একটি অসীম দৈর্ঘ্য এর চার্জিত রেখার থেকে r m দূরে কোনো একটি বিন্দুতে তড়িৎক্ষেত্র E এর মান কত? (দেওয়া আছে রৈখিক চার্জ ঘনত্ব λ C/m)
![]()
সমাধান:
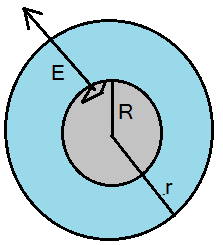
যেহেতু চার্জ সুষমভাবে বণ্টিত আছে তাই, ![]() এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর বাইরের দিকে। Gaussian surface হিসেবে আমরা একটা r ব্যাসার্ধ আর h উচ্চতার সিলিণ্ডার বেছে নিলাম। বৃত্তাকার প্রান্ত দিয়ে flux এর মান শূন্য কারণ বৃত্তাকার প্রান্তগুলোর সাথে
এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর বাইরের দিকে। Gaussian surface হিসেবে আমরা একটা r ব্যাসার্ধ আর h উচ্চতার সিলিণ্ডার বেছে নিলাম। বৃত্তাকার প্রান্ত দিয়ে flux এর মান শূন্য কারণ বৃত্তাকার প্রান্তগুলোর সাথে ![]() লম্বভাবে ক্রিয়া করছে। তাই আমাদের surface এর ক্ষেত্রফল হবে
লম্বভাবে ক্রিয়া করছে। তাই আমাদের surface এর ক্ষেত্রফল হবে ![]() । গাউসের Law অনুসারে,
। গাউসের Law অনুসারে,

সমস্যা- ৫: অসীম দৈর্ঘ্য এবং প্রস্থ এর নগণ্য পুরুত্বের চার্জিত sheet
একটি অসীম দৈর্ঘ্য এবং প্রস্থ এর নগণ্য পুরুত্বের চার্জিত sheet থেকে r m দূরে কোনো একটি বিন্দুতে তড়িৎক্ষেত্র E এর মান কত? (দেওয়া আছে ক্ষেত্র চার্জ ঘনত্ব λ C/m2)
সমাধান:
যেহেতু চার্জ সুষমভাবে বণ্টিত আছে তাই, ![]() এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর বাইরের দিকে। Gaussian surface হিসেবে আমরা একটা 2r উচ্চতা আর A প্রস্থচ্ছেদের ক্ষেত্রফল বিশিষ্ট pillbox বেছে নিলাম।
এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর বাইরের দিকে। Gaussian surface হিসেবে আমরা একটা 2r উচ্চতা আর A প্রস্থচ্ছেদের ক্ষেত্রফল বিশিষ্ট pillbox বেছে নিলাম। ![]() বক্রতলকে ছেদ করবে না বরং তা বৃত্তাকার প্রান্ত দিয়ে লম্বভাবে বেরিয়ে যাবে। গাউসের Law অনুসারে,
বক্রতলকে ছেদ করবে না বরং তা বৃত্তাকার প্রান্ত দিয়ে লম্বভাবে বেরিয়ে যাবে। গাউসের Law অনুসারে,

surface এর ক্ষেত্রফল 2A হল কেন? তার কারণ A দ্বারা আবদ্ধ চার্জ এর জন্যে দুইপাশেই সমান পরিমাণ তড়িৎক্ষেত্র পাওয়া যাবে সেজন্যেই 2A হয়েছে। আর এখানে E কিন্তু একপাশের একটা A এর মধ্যে দিয়ে তড়িৎক্ষেত্র তা মনে রেখ কিন্তু।
সমস্যা- ৬: একটি চার্জিত পরিবাহী
একটি চার্জিত পরিবাহী থেকে অল্প দূরে পৃষ্ঠের কাছাকাছি কোনো একটি বিন্দুতে তড়িৎক্ষেত্র E এর মান কত? (দেওয়া আছে ক্ষেত্র চার্জ ঘনত্ব λ C/m2)
সমাধান:
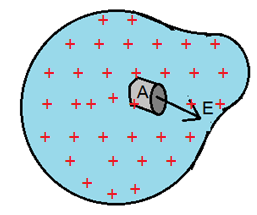
পৃষ্ঠের কাছাকাছি বিন্দুগুলোর জন্যে তড়িৎক্ষেত্র পৃষ্ঠের সাথে লম্বভাবে ক্রিয়া করে। এখন তড়িৎক্ষেত্র যদি লম্বভাবে ক্রিয়া না করে তাহলে surface বরাবর তার একটা উপাংশ থাকবে যা পরিবাহীর মধ্যে দিয়ে তড়িৎপ্রবাহ তৈরি করবে। যেহেতু এরকম কিছু ঘটছে না তাই বলা যায় তড়িতক্ষেত্র লম্বভাবেই ক্রিয়া করছে।এক্ষেত্রও আমরা Gaussian surface হিসেবে একটা A প্রস্থচ্ছেদের ক্ষেত্রফল বিশিষ্ট pillbox বেছে নিলাম। কিন্তু যেহেতু পরিবাহীর ভিতরে কোন চার্জ থাকে না সব চার্জ পৃষ্ঠে থাকে তাই পরিবাহীর ভিতরে pillbox এর অংশে কোনো তড়িৎক্ষেত্র থাকবে না। কেবল বাইরের দিকেই তড়িৎক্ষেত্র পাওয়া যাবে। গাউসের Law অনুসারে,
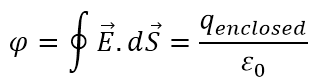

আগের সমস্যাটির সাথে এবারের সমস্যাটির পার্থক্য হল কেবল আগের বার দুইপাশেই তড়িৎক্ষেত্র পাওইয়া যাওয়ায় তড়িৎক্ষেত্রের মান অর্ধেক এসেছিল।
সমস্যা- ৭: আসীম দৈর্ঘ্যের চার্জিত সিলিণ্ডার
একটি অসীম দৈর্ঘ্য এর সিলিণ্ডার যার ব্যাসার্ধ R সিলিণ্ডার এর অক্ষ থেকে একটি দূরত্ব r এ E এর মান কত হবে? দেওয়া আছে, সিলিণ্ডারে চার্জ সুষমভাবে বণ্টিত আছে আর চার্জ ঘনত্ব ρ
(i) যখন r < R (ii) যখন r > R
সমাধান:
গাউসের Law অনুসারে,
(i)
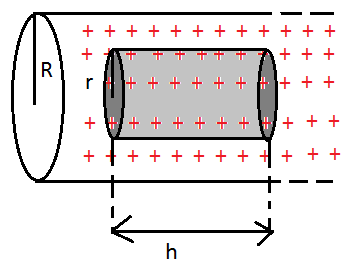
প্রথমে অসীম দৈর্ঘ্য এর সিলিণ্ডারটির ভিতরে h উচ্চতা এবং r ব্যাসার্ধের একটি ছোট সিলিণ্ডার বিবেচনা করি। ছোট সিলিণ্ডার এর বাইরের চার্জগুলো এর তড়িৎক্ষেত্রে কোনো প্রভাব ফেলবে না। আর ছোট সিলিণ্ডার এর সব জায়গায় তড়িৎক্ষেত্র হবে পৃষ্ঠের লম্ব বরাবর বাইরের দিকে। আর বৃত্তাকার পৃষ্ঠ দুটোয় flux বিপরীত হওয়ায় কেবল বক্রতলের মধ্যে দিয়ে flux ই হবে ছোট সিলিণ্ডারের flux।

(ii)
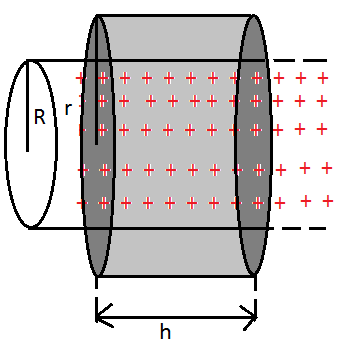
এবার অসীম দৈর্ঘ্য এর সিলিণ্ডারটির বাইরে h উচ্চতা এবং r ব্যাসার্ধের একটি বড় সিলিণ্ডার বিবেচনা করি। বড় সিলিণ্ডার এর ভিতরের চার্জগুলোই এর তড়িৎক্ষেত্রে প্রভাব ফেলবে । আর বড় সিলিণ্ডার এর সব জায়গায় তড়িৎক্ষেত্র হবে পৃষ্ঠের লম্ব বরাবর বাইরের দিকে। আর বৃত্তাকার পৃষ্ঠ দুটোয় flux বিপরীত হওয়ায় কেবল বক্রতলের মধ্যে দিয়ে flux ই হবে বড় সিলিণ্ডারের flux।

সমস্যা- ৮: আসীম দৈর্ঘ্যের সমকেন্দ্রিক দুইটি চার্জিত সিলিণ্ডার
দুইটি সমকেন্দ্রিক অসীম দৈর্ঘ্য এর সিলিণ্ডার যাদের ব্যাসার্ধ a এবং b (a < b) এবং উভয়ে সমান পরিমাণ চার্জে চার্জিত (প্রতি একক দৈর্ঘ্যে চার্জের পরিমাণ λ)। সিলিণ্ডার দুইটির অক্ষ থেকে একটি দূরত্ব r এ E এর মান কত হবে?
(i) যখন r < a (ii) যখন r > b (iii) যখন a < r < b
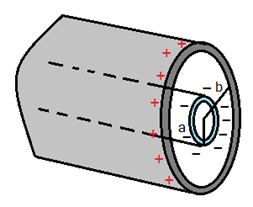
সমাধান:
গাউসের Law অনুসারে,
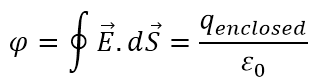
(i) r < a এর জন্য এর E মান হবে শুন্য কারণ Gaussian surface হিসেবে একটি সিলিণ্ডার বিবেচনা করলে তার মধ্যে কোনো আবদ্ধ চার্জ থাকে না।
(ii) আবার r > b এর জন্যেও E এর মান হবে শুন্য কারণ Gaussian surface হিসেবে একটি সিলিণ্ডার বিবেচনা করলে তার মধ্যে কোনো net আবদ্ধ চার্জ থাকে না অর্থাৎ সমান পরিমাণ ধনাত্মক ও ঋণাত্মক চার্জ থাকায় মোট চার্জ হয়ে যায় শুন্য আর তাই তড়িৎক্ষেত্র আর flux উভয়েই শুন্য।
(iii) a < r < b এর জন্য
Gaussian surface হিসেবে একটি সিলিণ্ডার (বেগুনি রঙের) বিবেচনা করলে সমস্যাটি অসীম দৈর্ঘ্য এর চার্জিত রেখার মত হয়ে যায় কারণ চার্জগুলো সমভাবে বণ্টিত এবং কেবল ঋণাত্মক চার্জগুলোই তড়িৎক্ষেত্র তৈরির জন্যে দায়ী। অর্থাৎ,

সমস্যা- ৯: চার্জ যখন ঘনকের কেন্দ্রে
একটি ঘনকের (যার বাহুর দৈর্ঘ্য a একক) কেন্দ্রে q C এর একটি চার্জ রাখা আছে। ছায়াকৃত অংশটির মধ্যে দিয়ে flux নির্ণয় কর।
সমাধান:
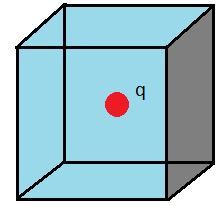
গাউসের Law অনুসারে,
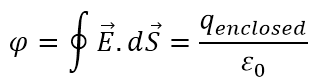
এখন যেহেতু চার্জটি ঘনকের ঠিক কেন্দ্রে অবস্থিত তাই এর 6 টি surface দিয়ে ঠিক সমান পরিমাণ flux হবে। তাহলে ঘনকটির 6 টি surface এর মধ্যে দিয়ে মোট flux হল
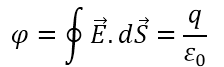
অর্থাৎ একটি surface এর মধ্যে দিয়ে বা ছায়াকৃত অংশের মধ্যে দিয়ে flux হবে মোট flux এর 6 ভাগের এক ভাগ।
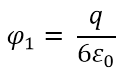
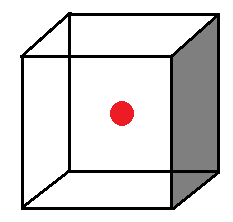
সমস্যা- ১০: চার্জ যখন ঘনকের শীর্ষে
একটি ঘনকের (যার বাহুর দৈর্ঘ্য a একক) একটি শীর্ষে q C এর একটি চার্জ রাখা আছে। ছায়াকৃত অংশটির মধ্যে দিয়ে flux নির্ণয় কর।
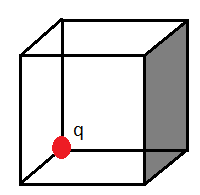
সমাধান:
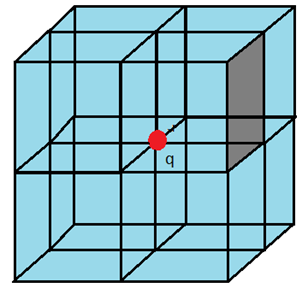
গাউসের Law অনুসারে,
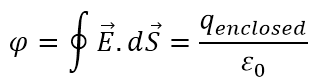
এখন যেহেতু চার্জটি ঘনকের ঠিক এক শীর্ষে আছে তাহলে এখন আর আগের মত সব দিয়ে সমান হবে না। কিন্তু চার্জটি যদি ঘনকের কেন্দ্রে থাকতো তাহলে আগের মত কত সহজেই না করে ফেলা যেত? তাহলে আমরা এবার চার্জটিকে একটি বড় ঘঙ্কের কেন্দ্রে ভাবলাম (ছবির মত)।
এখন যেহেতু চার্জটি বড় ঘনকের ঠিক কেন্দ্রে অবস্থিত তাই এর 6 টি surface দিয়ে ঠিক সমান পরিমাণ flux হবে। তাহলে ঘনকটির 6 টি surface এর মধ্যে দিয়ে মোট flux হল
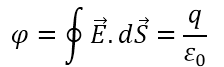
অর্থাৎ বড় ঘনকের একটি surface এর মধ্যে দিয়ে flux হবে মোট flux এর 6 ভাগের এক ভাগ।
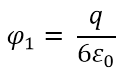
এখন তাহলে বড় ঘনকের প্রতি পৃষ্ঠে মোট ছায়াকৃত অংশের সমান ক্ষেত্রফলবিশিষ্ট surface আছে 4 টি তাহলে মোট ছায়াকৃত অংশের সমান ক্ষেত্রফলবিশিষ্ট surface আছে (6 × 4) বা 24 টি.

সমস্যা- ১১: সুষম তড়িৎক্ষেত্রে hemisphere এবং flux
একটি hemisphere এর ব্যাসার্ধ R এবং এটি এর অক্ষের সমান্তরালে একটি E মানের সুষম তড়িৎক্ষেত্রের মধ্যে অবস্থিত। এর মধ্যে দিয়ে flux নির্ণয় কর।
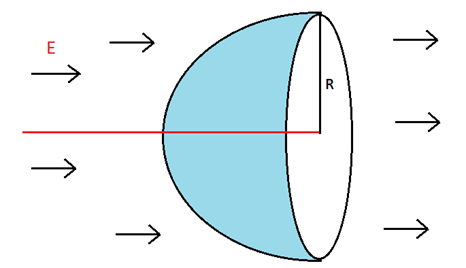
সমাধান:
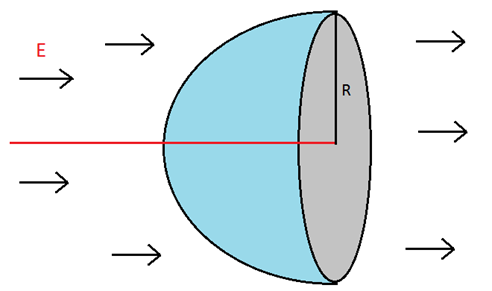
গাউসের Law অনুসারে,
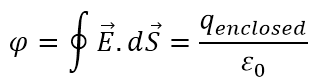

সমস্যা- ১২: গাউসের Law থেকে নিউটনের মহাকর্ষীয় সূত্র
পৃথিবী সুষম গোলক আর এর ভর m আর ব্যাসার্ধ R

সমাধান:
gravitational field এর জন্যে, গাউসের Law অনুসারে,
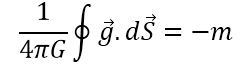

সমস্যা- ১৩: অসীম দৈর্ঘ্য এর রেখার জন্যে মহাকর্ষীয় ক্ষেত্র
একটি অসীম দৈর্ঘ্য এর রেখার থেকে r m দূরে কোনো একটি বিন্দুতে মহাকর্ষীয় ক্ষেত্র g এর মান কত? (দেওয়া আছে রৈখিক ঘনত্ব ρ kg/m)
![]()
সমাধান:
যেহেতু ভর সুষমভাবে বণ্টিত আছে তাই, ![]() এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর ভিতরের দিকে। Gaussian surface হিসেবে আমরা একটা r ব্যাসার্ধ আর h উচ্চতার সিলিণ্ডার বেছে নিলাম। বৃত্তাকার প্রান্ত দিয়ে flux এর মান শূন্য কারণ বৃত্তাকার প্রান্তগুলোর সাথে
এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর ভিতরের দিকে। Gaussian surface হিসেবে আমরা একটা r ব্যাসার্ধ আর h উচ্চতার সিলিণ্ডার বেছে নিলাম। বৃত্তাকার প্রান্ত দিয়ে flux এর মান শূন্য কারণ বৃত্তাকার প্রান্তগুলোর সাথে ![]() লম্বভাবে ক্রিয়া করছে। তাই আমাদের surface এর ক্ষেত্রফল হবে
লম্বভাবে ক্রিয়া করছে। তাই আমাদের surface এর ক্ষেত্রফল হবে ![]() । gravitational field এর জন্যে, গাউসের Law অনুসারে,
। gravitational field এর জন্যে, গাউসের Law অনুসারে,
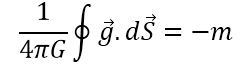

সমস্যা- ১৪: অসীম দৈর্ঘ্য এবং প্রস্থ এর নগণ্য পুরুত্বের sheet
একটি অসীম দৈর্ঘ্য এবং প্রস্থ এর নগণ্য পুরুত্বের sheet থেকে r m দূরে কোনো একটি বিন্দুতে মহাকর্ষীয় ক্ষেত্র g এর মান কত? (দেওয়া আছে ভরের ক্ষেত্র ঘনত্ব ρ kg /m2)

সমাধান:
যেহেতু ভর সুষমভাবে বণ্টিত আছে তাই, ![]() এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর ভিতরের দিকে। Gaussian surface হিসেবে আমরা একটা 2r উচ্চতা আর A প্রস্থচ্ছেদের ক্ষেত্রফল বিশিষ্ট pillbox বেছে নিলাম।
এর মান ধ্রুবক এবং তা পৃষ্ঠের লম্ব বরাবর ভিতরের দিকে। Gaussian surface হিসেবে আমরা একটা 2r উচ্চতা আর A প্রস্থচ্ছেদের ক্ষেত্রফল বিশিষ্ট pillbox বেছে নিলাম।![]() বক্রতলকে ছেদ করবে না বরং তা বৃত্তাকার প্রান্ত দিয়ে লম্বভাবে ভিতরে প্রবেশ করবে। gravitational field এর জন্যে, গাউসের Law অনুসারে,
বক্রতলকে ছেদ করবে না বরং তা বৃত্তাকার প্রান্ত দিয়ে লম্বভাবে ভিতরে প্রবেশ করবে। gravitational field এর জন্যে, গাউসের Law অনুসারে,
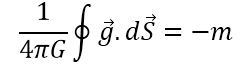

সমস্যা- ১৫: hollow spherical shell:
একটি ফাপা গোলকের ভিতরে তড়িৎক্ষেত্র এবং মহাকর্ষীয় ক্ষেত্র কত? (গোলকের ব্যাসার্ধ r, গোলকের পৃষ্ঠের চার্জ q C এবং ভর m kg)

সমাধান:
Gaussian surface হিসেবে আমরা একটা R ব্যাসার্ধ বিশিষ্ট গোলক (নীলটি) বেছে নিলাম।
এখন যেহেতু নীল গোলকের ভিতরে কোনো ভর বা চার্জ নেই তাই flux এবং তড়িৎক্ষেত্রের বা মহাকর্ষীয়ক্ষেত্রের মান হবে শুন্য।
একটি ফাপা গোলকের ভিতরে তড়িৎক্ষেত্র এবং মহাকর্ষীয় ক্ষেত্র শুন্য।
গাউসের Law এর তাৎপর্য:
আমরা এতক্ষণ গাউসের Law নিয়ে আলোচনা করলাম এবং গাউসের Law ব্যবহার করে বেশকিছু সমস্যার সমাধান করলাম। কিন্তু আসলে গাউসের Law এর তাৎপর্য টা কি? এটা আসলে কি বলে? এটা কি কেবলই flux, charge আর তড়িৎক্ষেত্রের মধ্যে সম্পর্ক স্থাপন করে? :/
তড়িৎক্ষেত্রের জন্যে গাউসের Law এর অর্থ হল electric monopole এর অস্তিত্ব আছে, electric চার্জ একা থাকতে পারে, অর্থাৎ ধনাত্মক ও ঋণাত্মক চার্জ পৃথকভাবে থাকে।
চৌম্বকক্ষেত্রের জন্যে গাউসের Law এর অর্থ হল magnetic monopole এর অস্তিত্ব নেই, magnetic pole একা থাকতে পারে না, অর্থাৎ কখনই North বা South pole পৃথকভাবে পাওয়া সম্ভব নয়।
মহাকর্ষীয়ক্ষেত্রের জন্যে গাউসের Law এর অর্থ হল ভরের monopole এর অস্তিত্ব আছে, ভর একা থাকতে পারে আর সামনে ঋণাত্মক চিহ্নের অর্থ হল মহাকর্ষীয়ক্ষেত্র সর্বদা আকর্ষণধর্মী।
আজ তাহলে এ পর্যন্তই। আশা করি বুঝতে পেরেছো, না বুঝতে পারলে অবশ্যই জানাবে কিন্তু। 😀

গাউসের সূত্র আসলে ফিজিক্স থেকে আসে না, এটা ভেক্টর এনালিসিসের এক্টা অংশ, আরো ভাল করে বললে ভেক্টর ক্যাল্কুলাস থেকে আসে । ফিজিক্স এর ভেক্ট্রর কোয়ান্টিটি’র এনালিসিসের জন্য আমরা এটা ব্যবহার করছি । সেহিসেবে প্রথম লাইনটা সংশোধন করলে ভাল হয় । অনেক বড় বিধাইয় পুরোটা পড়তে পারি নি ।
🙂 ইন্টার লেভেলে আমাদের নতুনযুক্ত করেছে এই চ্যাপ্টার। দারুণ বোঝা গেল। 😀