অনেক অনেক দিন পর আজ আমি আপনাদের সামনে আবার চলে এলাম। আসসালামু আলাইকুম।
জুনিয়র প্রোগ্রামাররা একটা ব্যাপার নিয়ে অনেক বেশি হিমশিম খায় প্রায়শঃ,আর এই ব্যাপারটা হচ্ছে বিশাল একটা সংখ্যার ভাগশেষ যখন বের করতে দেয়া হয়!! যদি কেউ বলে , ”এই প্রোগ্রামার,১০^১৮ কে ২৪৩৫৪৫৪ দিয়ে ভাগ করলে ভাগশেষ কত হবে বল তো?” , তুমি কিন্তু নিশ্চিন্তে “%” অপারেটরের সাহায্যে এক লাইন কোডের মাধ্যমেই উত্তর বলে তাকে চমকে দিতে পারো!
কিন্তু আমি এখন যদি তোমাকে প্রশ্ন করি “হে প্রোগ্রামার,আমাকে কি তুমি বলতে পারবে যে 9593875235847657867596748956485645786579687567485365467589756872782786735578344786757846548578345835849754 কে 13235 দিয়ে ভাগ করলে ভাগশেষ কত আসবে?”
তাহলে তুমি এবার নড়ে চড়ে বসবে,আমার তাই মনে হয়।
যদি নড়েচড়েই বসে থাকো,তাহলে আজকের এই পর্ব ঠিক তোমার জন্যেই আমি লিখছি।
একটা ব্যাপার খেয়াল করে দেখো,আমি যদি তোমাকে হাতে কলমে এই বড় সংখ্যাটাকে ভাগ করে ভাগশেষ বের করতে বলতাম,তুমি কিন্তু সেটা করতে পারতে। সময় লাগতো অনেক,তবে তুমি কিন্তু সংখ্যাটার শুরু থেকে ভাগ করতে করতে একসময় ভাগের কাজটা ঠিকই শেষ করে ফেলতে!! শুধু বড় সংখ্যাটায় যতগুলো অংক রয়েছে,তোমাকে সেই কয়টা ধাপে কাজ করা লাগতো খুব বেশি হলে!!
আচ্ছা,ছোট বেলার এই ভাগ করার নিয়মটা কি আমরা প্রোগ্রামিং এ ইমপ্লিমেন্ট করে দিতে পারিনা? করে ফেলতে পারিনা বিশাল বিশাল ভাগের কাজ? হ্যা অবশ্যই পারি,তার আগে আমি তোমাদের কে আরেকবার ছোটবেলার সেই ভাগ করার প্রসেসটা শিখিয়ে যেতে চাইঃ
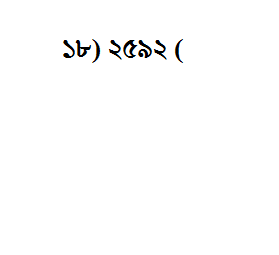
২৫৯২ কে আমরা ১৮ দিয়ে ভাগ করতে চাই
প্রথম ধাপটায় আমরা করবো কি,২৫৯২ এর শুরু থেকে চেক করতে থাকবো কখন সংখ্যাটা ১৮ বা তার চেয়ে বড় হয়,যখনি তা হবে,আমরা তাকে ১৮ দিয়ে ভাগ করে ভাগফলটাকে একদমমমমমমম ডানদিকে নিয়ে রেখে দিবো! 😀 আর ভাগশেষ বেচারাকে নিচে নিচে লিখতে থাকবো। দাঁড়াও,ছবি দিই আরোঃ

প্রথম ধাপ
আচ্ছা,প্রথম ক্ষেত্রে ভাগশেষ পেলাম ৭ , আর ভাগফল পেলাম ১ । খুব ভালো কথা। এবার আমরা এই প্রক্রিয়াটাকে আরো সামনের দিকে টেনে নিয়ে যেতে চাই। পরের ধাপঃ
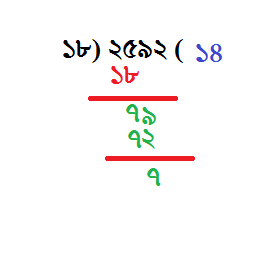
দ্বিতীয় ধাপ
আমরা সর্বশেষ ধাপে ভাগশেষ পেয়েছিলাম ৭। এর পাশে ৯ জুড়ে দিয়ে আমরা পেয়ে গেলাম ৭৯। আমরা এবার দেখবো,এর মধ্যে ১৮ কয়বার যায়! আচ্ছা,আমরা এইযে ৭৯ বানালাম,এটাকে গণিতের ভাষায় কীভাবে ব্যাখ্যা করা যায়?
” ঠিক আগের ধাপে আমরা যেই ভাগশেষটা পেলাম,তার সাথে ১০ গুণ দিয়ে উপর থেকে পরবর্তী ডিজিটটা যোগ করে দিলেই আমরা সংখ্যাটা পেয়ে যাই!! “
দেখো,ভাগশেষ এর আগের ধাপে ছিলো ৭,করলাম গুণ ১০,এর সাথে যোগ দিলাম উপর থেকে নেমে আসা ৯ কে,পেয়ে গেলাম ৭৯ 😀 এই লাইনটুকু মনে রেখো,এটাই আমাদের প্রোগ্রাম লিখার মূল মন্ত্র হবে।
এরপরের ধাপটা কি হতে পারে আশা করি বুঝে গেছো,তাও ছবি দিয়ে দিচ্ছিঃ
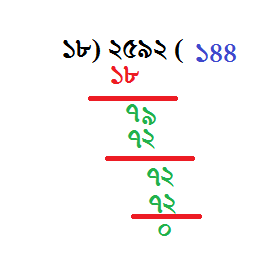
শেষ ধাপ
এভাবে যেতে যেতে একেবারে যখন উপর থেকে আর কোনো অংকই নেমে আসবেনা,তখন যেই ভাগশেষটা থেকে যাবে,সেটিই আমাদের কাঙ্ক্ষিত উত্তর। আমরা এই প্রক্রিয়াটিকে এবার সাধারণ ভাষায় লিখার চেষ্টা করি।
প্রথমে ভাগশেষকে ধরে নিই ০
এবার বিশাল সংখ্যাটার ( ভাজ্য ) শুরু থেকে শেষ অংক অবধি ঘুরে ঘুরে নিচের কাজটাই করবোঃ
ভাগশেষ =( ভাগশেষ* ১০ ) + উপর থেকে নেমে আসা অংক ) % ভাজক
এভাবে প্রতিবার চেক করে যাব,কখনো কি আমাদের ”ভাগশেষ” নামক সংখ্যাটা ভাজক দিয়ে নিঃশেষে বিভাজ্য হয় কিনা,যদি ”ভাগশেষ” নামক সংখ্যাটা ভাজকের চাইতে ছোট হয়,তাহলে আমরা তাকে পরবর্তী ধাপে carry (বহন) করে নিয়ে যাবো,আর যদি ভাজকের চেয়ে বড় হয়ে যায়,তাহলে তাকে ভাগ দিয়ে ভাগশেষটাকে পরবর্তী ধাপে নিয়ে যাব। হাতে কলমে আমরা কিন্তু এই সহজ কাজটাই করে যাই। 🙂
ওহ আচ্ছা,গুরুত্বপূর্ণ কথা। আমাদের এই প্রক্রিয়াটি কাজে দিবে তখনি,যখন ভাজক ১০^১৮ এর সমান বা তার চেয়ে ছোট হবে। তবে ভাজ্য যত খুশি বড় হোক,আমাদের তাতে কোনো সমস্যা নেই! 😀 ( যত খুশি তত বড় বলতে = হাইয়েস্ট ক্যারেক্টার এ্যারে সাইজ )
তাহলে আমাদের এলগোটা কেমন হবে? চলো দেখে আসিঃ
#include <stdio.h>
#include <string.h>
int main()
{
char bhajjo[1000];
long long i,bhajok,bhagshesh=0;
scanf("%s",bhajjo);
scanf("%lld",&bhajok);
int l=strlen(bhajjo);
for(i=0; i<l; i++)
{
bhagshesh = ((bhagshesh*10) + (bhajjo[i]-'0') )%bhajok; // Amra character theke integer e convert kore nilam '0' biyog kore
}
printf("%lld\n",bhagshesh);
return 0;
}
এর সাহায্যে তোমরা lightoj 1078 সল্ভ করে ফেলতে পারো।।
আজকের মত এটুকুই। মতামত জানাতে ভুলো না!
আর,ভাগশেষ কিন্তু সবসময় এক ডিজিটের হয়না,এইটা রূপক অর্থে দেয়া :p
পরবর্তী পর্বে আমরা আলোচনা করেছি ভাগফল নিয়ে! 😀


খুবই ভালো লাগলো ভাই আপনার লেখা পড়ে 😀 । অনেক কিছু মজার একটা লেখা , অনেক সহজ উপস্থাপন । 🙂
তবে আমরা তো কচি-কাঁচা কেবল শুরু করেছি তাই একটু সহজ করে ব্যখ্যা যদি দিতেন যে স্ট্রিং হেডার ছারাও আমাদের কম্পাইলার কেন একটা এরর রিপোর্ট দিয়ে কোডটা রান করবে …
আর bhajjo[i]-‘0’ এই অংশটা একটু বুঝিয়ে দিয়েন যে ক্যানো ascii থেকে ৪৮ বিয়োগ দিচ্ছি, বা ওই অংশে কি char ই থাকছে নাকি int এ রূপান্তর হচ্ছে । আমাদের মত অনেক নবীনদের এতে একটু সুবিধা হয় , বিশেষত আমরা যারা cse পড়ি নাই।
আরো লিখা চাই , আরো জানতে চাই , স্বশিক্ষায় শিক্ষিত হতে চাই ।
ভালোবাসা জানবেন ।
ধন্যবাদ ভাইয়া,
আমাদের CodeBlocks এ কিছু ছোটখাটো হেডার ফাইল জনিত ইরোর অটোমেটিক ডিটেক্ট করে কারেক্ট করে দেয়,তবে অনলাইন জাজ গুলোতে এই ঘটনা টা ঘটে না।
আর ASCII থেকে ৪৮ কেন বিয়োগ করলামঃ
ক্যারেক্টার ‘0’ হচ্ছে ইন্টেজারে 48 , ‘1’ হচ্ছে 49 এভাবে ‘9’ হচ্ছে 57 । আমার যেহেতু যোগ বিয়োগ গুণ ভাগ এইসব এরিথমেটিক অপারেশন চালাতে হবে,তাই আমি ক্যারেক্টার থেকে ৪৮ বিয়োগ দিয়ে এদের ইন্টেজারে রুপান্তর করে নিয়েছি।
ক্যারেক্টারে ‘5’ , ইন্টেজারে 5
সুতরাং, ‘5’ – 48 = 5
আশা করি বুঝেছো 🙂
valo lagse (y)
🙁
অসাধারন একটা লিখা ভাইয়া <3
uva 10929 ai problem ta add kortay paren