আমি যখন ইন্টারমিডিয়েট পরীক্ষা দিবো,তখন ফিজিক্স দ্বিতীয় পত্রের কিছু চ্যাপ্টারের প্রতি খুব গভীর দুর্বলতা কাজ করতো!!তাঁর মধ্যে একেবারে শুরুর দিকের যদি একটা চ্যাপ্টারের নাম বলি,তাহলে সেটা চলতড়িৎ চ্যাপ্টারটা হবে!
বিভিন্ন রকম সার্কিট,সেগুলার তুল্য রোধ বের করা,এই তাড় দিয়ে কতোটুক বিদ্যুৎ গেলো,ওইটা দিয়ে কতটুক গেলো,এইসব প্রথম প্রথম খুব ভালো লাগতো! প্রচণ্ড কনফিডেন্টলি বোর্ড লেভেল পর্যন্ত কাভার করে আসলেও একটু বিপাকে পড়ি যখন এডমিশনের সময় আসে। ইঞ্জিনিয়ারিং কোচিং করার দরুণ এসব নিয়ে একটু বেশিই ঘাটাঘাটি হয় অনেকের। তখন এমন কিছু সার্কিট এর সামনে এসে পড়তে হয়,যেগুলা না পারা যায় স্বাভাবিক তুল্যরোধের প্রসেসে সল্ভ করা,না পারা যায় KVL/KCL এর কিছু প্রাথমিক জ্ঞান দিয়ে সল্ভ করা। এসব জটিল ধরণের সার্কিট সল্ভ করার জন্য কিছু প্রসেসের মধ্যে আমি দু’টোর নাম বলিঃ
১) MESH ANALYSIS ( মেশ এনালাইসিস )
২) NODAL ANALYSIS ( নোডাল এনালাইসিস )
এছাড়া আরো নানা ধরণের কনভার্সন আছে যেমন ওয়াই-ডেলটা কনভার্সন,পাই-টি কনভার্সন। এসব আপাতত দরকার নেই। একদম খুব সহজ সরলভাবে মেশ এনালাইসিস নিয়ে আজ আলোচনা করবো খুবই ক্যাজুয়াল ওয়ে-তে। কারো যদি এসব নিয়ে বিস্তারিত পড়াশোনার ইচ্ছা থাকে,তাহলে নেট সার্চ করে Boylestad Sir এর বই দেখে নিতে পারো। গুগল করলে হাতের কাছেই এই বই পেয়ে যাবা।
যাই হোক,কথা না বাড়িয়ে একেবারে ছোট ছোট সহজ কিছু সমস্যা নিয়ে আলোচনায় চলে যাব। কিছু সমস্যা নিয়ে আলোচনা করলে তোমরা আজকের আলোচনার বিষয়বস্তু সম্পর্কে অবগত হতে পারবে। থিওরেটিকাল আলোচনা এখানে খুবই কম করা হবে,যেটা আগে থেকেই বলে রাখা হচ্ছে। টুকটাক প্রয়োজনীয় অংশ হাতের কাছে আসলেই বলে দেয়া হবে,আর কিছু হোমওয়ার্ক এর সুব্যবস্থাও থাকবে একেবারে শেষে!
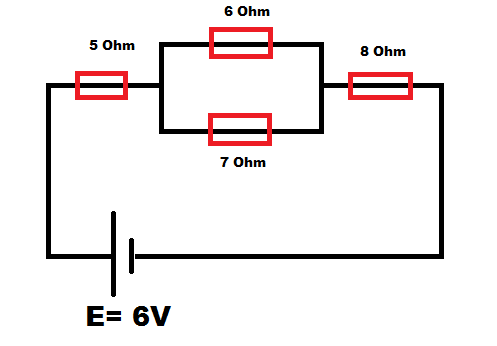
দেখো,একটা সহজ সার্কিটের ছবি তোমাদের সামনে নিয়ে আসলাম।
এই সার্কিটটা সল্ভ করে এর তুল্যরোধ বের করতে পারবে আশা করি। চিরায়িত সমান্তরাল আর শ্রেণী সমবায়ের ধারণা দিয়েই একেবারে সহজেই এটি সমাধান করা যায়! ৬ আর ৭ ওহম রোধ আছে সমান্তরালে,তাই এদের তুল্যরোধ বের করে এদের সাথে ৫ আর ৮ ওহম রোধ যোগ করে দিলেই আমরা মোট তুল্যরোধ পেয়ে যাবো! 😀
আচ্ছা বর্তনীর মোট তড়িৎপ্রবাহ যদি I হয়,সেটি কতো হবে?
I = E/R
ব্যাটারীর তড়িচ্চালক শক্তি এখানে E , আর অভ্যন্তরীণ রোধ ধরে নিলাম শুণ্য,যাতে আমাদের হিসাব সুবিধা হয়।
আচ্ছা,এখন এই সমস্যাটিকে আমরা একটু অন্যভাবে সল্ভ করি। লুপ ধরে কার্শফের সুত্র দিয়ে সমাধান করার প্রক্রিয়াটা মনে আছে তোমাদের? সার্কিটে লুপ ধরে ধরে আগানোর ব্যাপারটা?
ধরে নিই,এখানে লুপ রয়েছে দু’টি। আমরা দু’টি লুপ দেখে আসি।
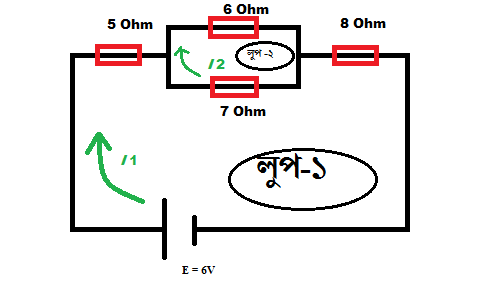
চিত্র : আগের সার্কিটটাকেই আমরা লুপ ধরে সল্ভ করার চেষ্টা করছি। দুইটা লুপ মার্ক করে দেয়া হয়েছে।
প্রথম লুপটির দিকে একটু তাকাই। লুপ ধরে সল্ভ করার প্রসেসে আমরা যখন একটি লুপ নিয়ে কাজ করবো,তখন ওই লুপটিতে কোনো তড়িচ্চালক শক্তি আছে কিনা সেটা বিবেচনায় আনবো,তড়িচ্চালক শক্তি যদি লুপটিতে না থাকে,তাহলে আমরা এর ভ্যালু উক্ত লুপটির জন্য শুণ্য ধরে কাজ করবো।
প্রথম লুপটি নিয়ে কাজ শুরু করা যাক!!
১ম লুপঃ
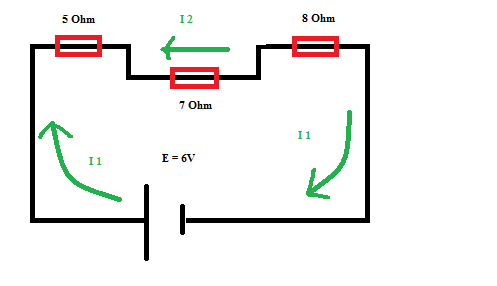
এই লুপটি দিয়ে i1 নামক কারেন্ট পাস হচ্ছে। একটু ছবির মাধ্যমে দেখে আসি।
এখানে দেখো,এই লুপটাতে ৫ , ৭ আর ৮ ওহম এর রোধ তিনটি আছে শ্রেণীতে,তাহলে এদের তুল্যরোধ হবে ( ৫ + ৭ + ৮) = ২০ ওহম।
তাহলে আমরা লিখতে পারি,
20 i1 – 7i2 = 6
আচ্ছা!! দাঁড়াও দাঁড়াও!! আমরা আবার 7i2 আনলাম কোত্থেকে? সেটাকে আবার বিয়োগই বা করলাম কেন???? 😮
দেখো,লুপ ২ এর কথাটা একবার চিন্তা করতে হবে এখন। আমরা যতগুলা লুপ ই নিই না কেন,সবগুলাতে কারেন্ট প্রবাহের দিক সবসময় একদিকেই ধরে নিবো। এখানে আমরা ঘড়ির কাটার দিকে ধরে নিয়েছিলাম। খেয়াল করে দেখো,লুপ ২ এ ৭ ওহম এর ভিতর দিয়ে i2 মানের কারেন্ট i1 এর বিপরীত দিক দিয়ে প্রবাহিত হচ্ছে। যেহেতু আমরা এখানে ধরেই নিয়েছি যে i1 কারেন্ট লুপ ১ দিয়ে প্রবাহিত হচ্ছে,অন্য কথায়,আমরা লুপ ১ এর কথা ই শুধু এখানে চিন্তা করছি,তাই আমরা i1 থেকে এই অতিরিক্ত i2 কারেন্ট এর মানটাকে বিয়োগ করে দিচ্ছি! 😀 কেননা তড়িৎপ্রবাহ তো ভেক্টর রাশি,তাইনা? বিপরীত দিকে চলমান একই মানের তড়িৎ প্রবাহ চললে আল্টিমেটলি নেট কোনো তড়িৎপ্রবাহই পাওয়া যাবেনা। আর যেহেতু একটি লুপে মোট সঞ্চিত বিভবের মান শূন্য,তাই 6 – 20i1+7i2=0 হওয়ার ই কথা!! KVL থেকে আমরা সেটাই জানি,খেয়াল করে দেখো,আমি উপরে এটাকেই একটু অন্যভাবে কেবল লিখেছি।
এখন লুপ ২ এর ক্ষেত্রে সমাধান করি চলো।
লুপ ২:
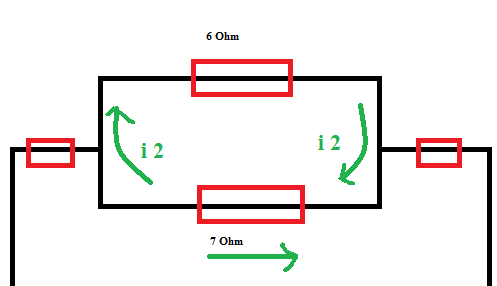
চিত্রঃ লুপ ২ নিয়ে ঘাঁটাঘাঁটি
এখানে কোনো তড়িচ্চালক শক্তি নেই। পুরো লুপের ভিতর দিয়ে i2 কারেন্ট প্রবাহিত হচ্ছে। ৭ ওহম রোধের ভিতর দিয়ে i2 এর বিপরীত পাশ দিয়ে i1 যাচ্ছে,তাই এটাকে বাদ দিতে হবে।
(6+7)i2 – 7i1=0
যেটাকে আমরা লিখতে পারি আরেকটু সুন্দর ভাবে,
13i2 – 7i1=0
এবার লুপ ১ আর ২ এর জন্য প্রাপ্ত সমীকরণ দুটিকে সমাধান করলে i1 আর i2 এর জন্য মান পাওয়া যাবে নিম্নরূপঃ
i1 =78/211 A
i2 =42/211 A
মজার শুরু এখন!! খেয়াল করে দেখো, i1 নামক যেই কারেন্টের ভ্যালু আমরা বের করলাম,সেটিই কিন্তু আসলে মূলপ্রবাহ!! 😀 চিত্র মিলিয়ে দেখো বিশ্বাস না হলে।
তাহলে , তুল্যরোধ টা হবে তড়িচ্চালক শক্তিকে এই i1 দ্বারা ভাগ করলে যা পাওয়া যাবে,সেটা।
R =6/(78/211) Ohm = 16.2307 Ohm
প্রথমবারে যখন তুল্যরোধ বের করেছিলো,তখন কি মান এটাই আসেনি? 😀
খুব সহজ একটা সমস্যার সমাধান নিয়ে আলোচনা করার এখনো হয়তো এর গুরুত্ব অনেকে ধরতে পারো নি। এবার একটু ঝামেলায় ফেলে দিই,তাহলেই গুরুত্ব উপলব্ধি করতে পারবে।
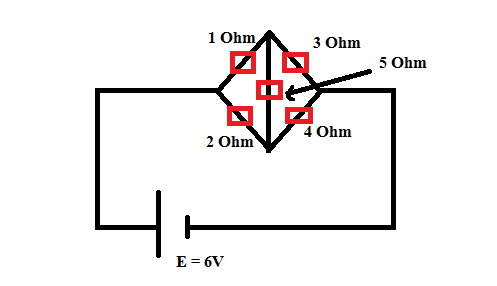
নিচের সার্কিটটা দেখোঃ
এই সার্কিটটা দেখে তোমাদের মনে হুইটস্টোন ব্রীজের কথা মনে আসতে পারে! কিন্তু হুইটস্টোন ব্রীজের শর্ত ছিলো,সেটা হচ্ছে বাহুগুলোতে বিদ্যমান রোধগুলোর অনুপাত সমান হতে হবে অপর দুইটি রোধের অনুপাতের। কিন্তু এখানে কিন্তু ওমনটি হয়নি,অনুপাত সমান নয়। তাই এখানে তুমি চিরায়ত নিয়মে সমাধান ও করতে পারবেনা।
তাহলে উপায় কি?
উপায় হচ্ছে লুপ ধরে মেশ চালায় দেয়া! 😀
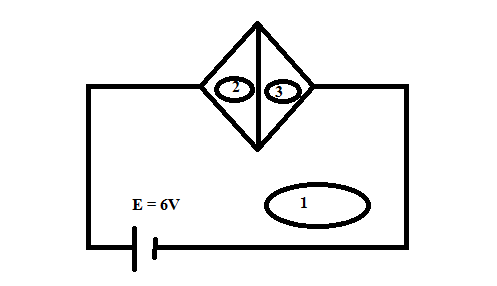
দেখো,এখানে আমাদেরকে তিনটি লুপ ধরতে হবে। দুইটি লুপ উপরের দুইটি ভাগে,আর আরেকটু লুপ তড়িচ্চালক উৎস টা কে নিয়ে থাকবে। এক কাজ করো,এতোটুক হিন্টস তো দিয়েই দিলাম,পারলে সল্ভ করার ট্রাই করো নিজে নিজে! 😀 ভয়ের কিছু নেই,আমি নিজেও সমাধান করে দিচ্ছি।
আমরা তিনটি লুপ এখানে আইডেন্টিফাই করে দিলাম।
১ নং লুপ দিয়ে ধরা যাক i1 কারেন্ট যায়।
২নং লুপ দিয়ে যায় i2
আর ৩নং লুপ দিয়ে যায় i3
আমি উপরে রোধগুলোকে উল্লেখ করিনি,শুধু লুপগুলো কোনটা কোনটা হবে তা দেখালাম। এবার সমাধান করা যাক।
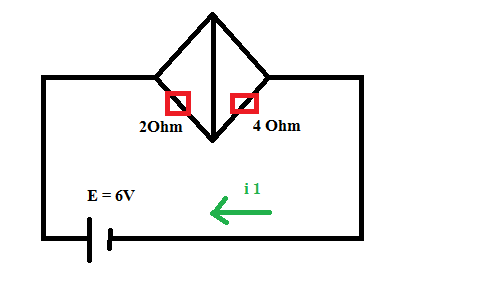
প্রথম লুপঃ
সমীকরণটি লিখে ফেলি।
(2+4)i1 – 2i2 -4i3 = 6
=> 6i1 – 2i2 – 4i3=6
কেন আমরা 2i2 আর 4i3 বিয়োগ দিলাম,তা প্রথম সমস্যাটার সমাধান বুঝলে বুঝার কথা। না বুঝলে আবার বলি,লুপ ২ আর লুপ ৩ এর ক্ষেত্রে i2 আর i3 পরিমান কারেন্ট ওই দুইটি রোধ দিয়ে যাচ্ছিল,যাদের মান কে আমাদের হিসাবের স্বচ্ছতার দরুন ই বাদ দিয়ে দেয়া হয়েছে। খেয়াল রাখতে হবে,আমরা কিন্তু তড়িৎপ্রবাহ বিয়োগ করছিনা! তড়িৎপ্রবাহের দরূন ওই রোধটির দুই প্রান্তে যেই পরিমাণ ভোল্টেজ ড্রপ হচ্ছে,সেটি বিয়োগ করছি। কারশফের ভোল্টেজ ল তো তাই বলে,না?
এবার দ্বিতীয় আর তৃতীয় লুপের জন্য ছবি আঁকবো না,ডিরেক্ট সমীকরণ লিখবো। ছবি তোমরা নিজে খাতায় আঁকার চেষ্টা করো,তারপর মিলিয়ে নাও।
8i2 – 2i1 – 5i3 = 0 (এটি ২নং লুপের জন্য)
12i3 – 5i2 – 4i1 = 0 (এটি ৩নং লুপের জন্য)
এবার আমরা তিনটি সমীকরণকে সুন্দরভাবে সাজাই।
6i1 – 2i2 – 4i2 = 6
-2i1 + 8i2 – 5i3=0
-4i1 – 5i2 + 12i3 = 0
অনেক সময়ই তড়িচ্চালক শক্তির মান দেয়া থাকেনা,তুমি নিজের ইচ্ছামত একটা মান ধরে সমাধান করবে। শেষে সেটি এমনিতেই বাদ পরে যাবে।
সমীকরণ ৩টিকে সমাধান করলে আমরা পাই:
i1 = 2.508A
i2=1.553A
i3= 1.482A
খেয়াল করে দেখো,i1 টাই হচ্ছে মূল প্রবাহ। 😀
তাই,তুল্যরোধের ক্ষেত্রে আমরা এখন আগের মতোই কাজ করবোঃ
R = 6/2.508 Ohm = 2.3944 Ohm
আজকের আলোচনা এতোটুকুই! তোমাদের কোনোকিছু বুঝতে অসুবিধা হলে বা আমার লিখাতে কোনো অসামাঞ্জস্য খুঁজে পেলে,কমেন্টে জানাতে দেরি করবেনা। আমরা পরবর্তীতে আরো কিছু প্র্যাকটিস প্রব্লেম সল্ভ করবো। 🙂


কার্শফের নীতি এর যথার্থ প্রয়োগ। এই টেকনি আগেও শিখছিলাম। কিন্তু বুঝার মধ্যে ঘাপলা ছিল বলে এপ্লাই করতে পারতাম না। এখন মনে হয় পারবো। ভাইয়া বেশি বেশি প্রবলেম আপলোড করলে ভালো হতো 😀
আজকে কালকের মধ্যেই দেয়া হবে। 😀
vaia aro circuit dan choromvabe bujsi … thanks 😀
খুবই সুন্দর হয়েছে। আমি ভালভাবে বুঝতে পেরেছি। আপনাকে ধন্যবাদ।।
thans vaieeeeeeeeeeeeeee…………