এই পর্বটি অনেকটা তাদেরকেই উদ্দেশ্য করে লিখা যারা গতি বিষয়ক সমস্যা সমাধানের সময়ে প্লট বা ক্ষেত্র নামক ব্যাপারটা চিন্তা না করেই সমস্যা সমাধান শুরু করে দেয়,এবং মাঝপথে এসে বিভ্রান্তিতে পড়ে যায় যে কোথায় এখন কোন সূত্র ব্যবহার করবে। আজকের পর্বটি শুরু করার আগে পদার্থবিজ্ঞানের গতিবিষয়ক (একমাত্রিক) সূত্রগুলো একটু স্মরণ করা যাকঃ
একটা কমন ভুল অনেককেই করতে দেখা যায়। আমাদের উপর্যুক্ত গতীয় সমীকরণগুলো কিন্তু “অসমত্বরণ” এর ক্ষেত্রে প্রযোজ্য নয়।! আরেকটা কথা,অনেকে গ্যালিলিওর পড়ন্ত বস্তুর সূত্রগুলোকে আলাদাভাবে স্মরণে রেখে কাজ করতে যায়। স্মরণে ঠিকঠাকভাবে রাখতে পারলে কারোই কোনো অসুবিধা নেই,আমাদেরও না,ফিজিক্সের ও না। তবে স্মরণে রেখে সেটা প্রয়োগ করার সময় ভুল করলে সমস্যা হতে পারে। তাই আমরা পড়ন্ত বস্তুর সূত্রগুলোকে আলাদাভাবে মনে না রেখে,এই ৪টি সূত্রের মাধ্যমেই বিস্তারিত জানার চেষ্টা করবো। এবং কিছু কিছু সমস্যার সমাধান কীভাবে গ্রাফ এঁকে খুব সহজেই সমাধান করা যায়,সেটাও কিছুটা জানার চেষ্টা করবো।
উপরের সূত্রগুলোর কোন প্রতীকটি কী নির্দেশ করে , তা আবার একটু দেখে নিইঃ
a = ত্বরণ
v = শেষবেগ
u = আদিবেগ
t = সময় s = সরণ
এবং , v(bar) = গড়বেগ
প্রশ্নঃ অসমত্বরণের জন্য তাহলে কী করবো ভাইয়া?
উত্তরঃ ক্যালকুলাস।
আমরা কয়েকটা সমস্যা নিয়ে আজকে একটু আলোচনা করি। এসব সমস্যা নিয়ে আলাপ করতে করতে আশা করা যায় যে আরো নতুন কিছু সমস্যার উদগীরণ হবে,প্রশ্নগুলোর উত্তর পাওয়া যাবে,ইত্যাদি।
সমস্যা নং ১ঃ
একটি হরিণ সুন্দরবনের একটি গহীন স্থানে বসে বিশ্রাম নিচ্ছে। হরিণটি থেকে ২০ মিটার দূরে ওত পেতে থাকা একটা বাঘ খুব শান্তমনে হরিণটিকে দেখছে,খাবে একটূপর আর কি! তো এবার বাঘটা করলো কি , ১০০ মি./সে.^২ সমত্বরণে হরিণটির দিকে এগিয়ে যেতে থাকলো। সেটি দেখে তৎক্ষণাৎ হরিণটি ১৫০ মি./সে. সমবেগে দৌড়াতে শুরু করলো। বলতে পারবে,বাঘটি হরিণটিকে ধরতে যদি পারে,কতক্ষণ পরে এবং কত দূরে গিয়ে ধরতে পারবে?
সমাধানঃ
আমরা এই সমস্যাটি ছবি-টবি এঁকে সমাধান করবো। আমি জানি সমস্যাটি অনেক বেশি সহজ,তবে আমার উদ্দেশ্য হচ্ছে এই সহজগুলো থেকেই ধীরে ধীরে আরেকটু কঠিনের দিকে মুভ করা। নিচের ছবিটি দেখি ঝটপটঃ
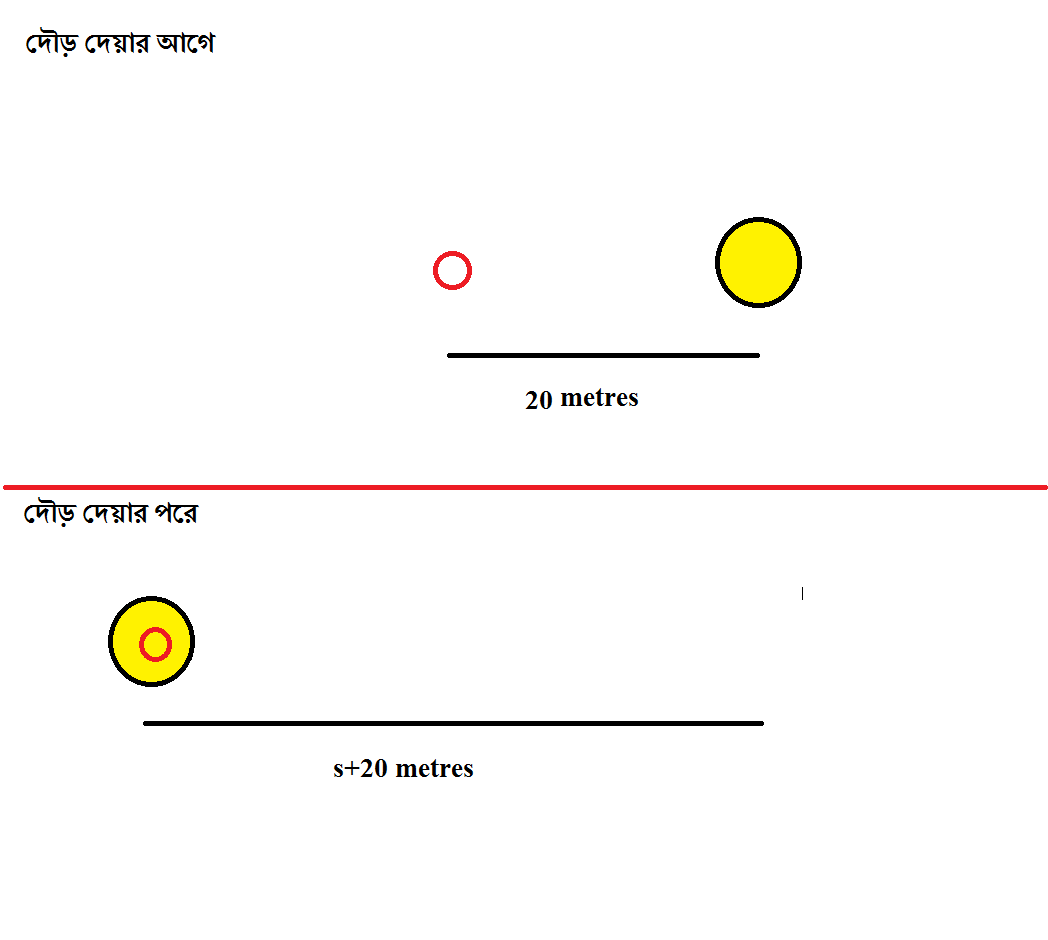
ধরে নিই যে হরিণটি তার বর্তমান অবস্থা থেকে ঠিক s দূরত্ব যাওয়ার পরেই বাঘটি ওর ঘাড় মটকে দিবে। আর বাঘের জন্য হবে সেটি s+20 মিটার। বাঘ শক্তিশালী,তাই একটু বেশি দূরত্ব তাকে শেষ করতে দিলে অসুবিধা কই? 😀 আসলে,সে ২০ মিটার পিছনে ছিলো বলে কথা।
তাহলে,বাঘের ক্ষেত্রে তার যাত্রাপথের সমীকরণটিকে আমরা লিখতে পারি এইভাবেঃ
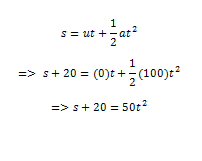
কারণ বাঘটি স্থির অবস্থা থেকে দৌড় দিয়েছে,আর হরিণের বেলাতেও একই ঘটনা,তবে তার দৌড় ছিলো সমবেগে,কোনো ত্বরণ টরণ নাই।
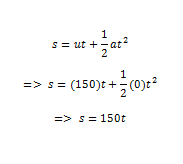
কাজ শেষ আমাদের। এখন এই দু’টো সমীকরণকে সমাধান করে ফেললেই আমরা আমাদের সব ধরণের উত্তর পেয়ে যাবো।
সমস্যা নং ২ঃ
এবারের সমস্যাটায় Twelve Grade এ এসেও অনেকে মাঝেমধ্যে একটু ঝামেলা পাকায়। ধরো তুমি গ্রামীণ ব্যাংকের উপরে দাঁড়িয়ে আছো! অনেক উঁচু কিন্তু,প্রায় ২০ তলার মতো। তো ছাদে দাঁড়িয়ে তুমি তোমার মাথার উপরের দিকে একটা বল ছুড়ে মারলে। বলটা একবারে সোজা উঠলো,তারপর সোজা একদম বিল্ডিং এর নিচে পড়লো। তুমি পুরোটা সময় স্টপওয়াচে মেপে নিলে। তোমার কাছে সময়টি তাহলে রেকর্ড করা আছে। তোমার উচ্চতা ৫ ফিট ৭ ইঞ্চি হলে,গ্রামীণ ব্যাংকের উচ্চতা কত? এ প্রশ্ন যদি তোমাকে করা হয়,তাহলে তুমি উত্তরটা দিতে পারবে সঠিকভাবে? ধরে নাও,বাতাসের বাধা অগ্রাহ্য করা হয়েছে।
ও আচ্ছা,বলটির উপরে উঠতে আর নিচে গিয়ে পড়তে পড়তে সময় লাগলো ধরো ৮ সেকেণ্ডের মতো। আর সে উপরে বলটাকে ২০ মি/সে বেগে ঢিল দিলো,g এর মান ও ধরো ১০মি/সে^২
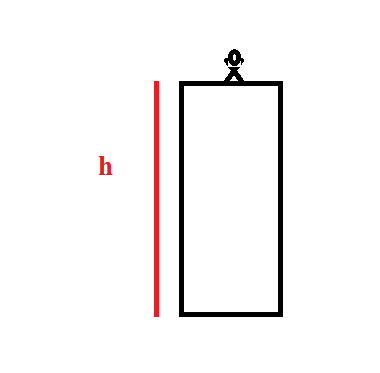
সমাধানটা কেমন হতে পারে? আমরা মুখে মুখে এগিয়ে যদি যাই প্রথমে…
প্রথমে ছেলেটা বলটাকে ২০মি/সে বেগে উপরে ঢিল দিবে। এতে বলটি একটি নির্দিষ্ট উচ্চতায় উঠবে,রাইট? এই পর্যন্ত আমরা একটা ফ্রেম বা দৃশ্যপট চিন্তা করবো। তারপরের ফ্রেমটা হবে এরকম,বলটি সেই উচ্চতা থেকে একেবারে নিচে পড়ে গেল। এই দুইটা ফ্রেমকে কোনোভাবে একসাথে লিংক করে ফেলতে পারলেই আমাদের সমস্যাটা পানির মতো সহজ হয়ে যাবে।
প্রথমে দেখি বলটা কতটুক উপরে উঠতে পারে। v = u-gt এই সূত্রে শেষবেগ যখন শূণ্য এবং আদিবেগ যখন উপস্থিত,তখন t = u/g । তার মানে আমাদের এই বলটি ঢিল দেয়ার পর ২০/১০ = ২ সেকেন্ড সময়ের মধ্যেই সবচেয়ে উঁচুতে উঠে যেতে পারবে! 😀 এবং ছাদ থেকে এই সবচেয়ে উঁচু পয়েন্টটা কত উঁচুতে সেটাও সহজে বের করে ফেলা যায় চাইলেই!
আমরা জানি,
 তাহলে বলটা কতটুক পর্যন্ত উঠতে পেরেছিলো? উত্তরঃ h = u^2/2g = ২০ মিটার। 😀
তাহলে বলটা কতটুক পর্যন্ত উঠতে পেরেছিলো? উত্তরঃ h = u^2/2g = ২০ মিটার। 😀
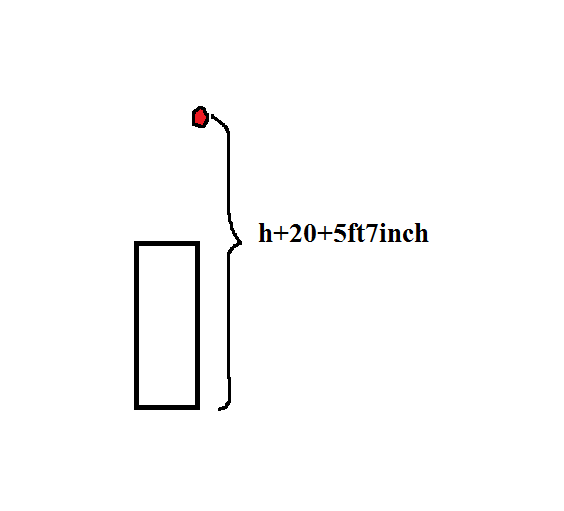
ছবিটি দেখো। বলটা এখন ভূমি থেকে (h+20)metre+5ft7inch উঁচুতে আছে! 😮 খেয়াল করো,আমরা কিন্তু ছেলেটার হাইট বলে দিয়েছিলাম যে ৫ ফিট ৭ ইঞ্চি,সেটিকেও এখন যোগ করে দিতে হবে! কেননা,যখন সে বলটা ছুড়ে দিয়েছে উপরের দিকে,তখন কিন্তু তার হাইট টা আসলে কোনো প্রভাবই ফেলে না! তবে যখন বলটি নেমে আসে,তখন তার হাইটের সমান পরিমাণ দূরত্ব তাকে অতিক্রম করে আসতে হয়। তাই এটি যোগ করতে হচ্ছে।
যাজ্ঞে,হিসেব করে দেখলাম ছেলেটার হাইটটা মিটারে নিলে আসে 1.7018 মিটারের মতো। একেবারে উঁচুতে বস্তুটি স্থির দাঁড়িয়ে আছে,তার মানে আদিবেগ শূণ্য। আমরা বলতে পারিঃ
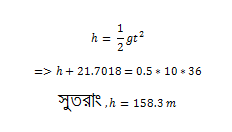
এখান থেকে ছেলেটার হাইট আর সেই ২০ মিটার অতিরিক্ত বাদ দিয়ে দিলেই আমাদের গ্রামীন ব্যাংকের হাইট পেয়ে যাবো। আর যদি বলে দিই,প্রতি তলার উচ্চতা ১০ ফিট,গ্রামীন ব্যাংক তাহলে কয় তলা? সেটার উত্তরও তোমরা দিয়ে দিতে পারবে খুব সহজে।
সমস্যা নং ৩ঃ
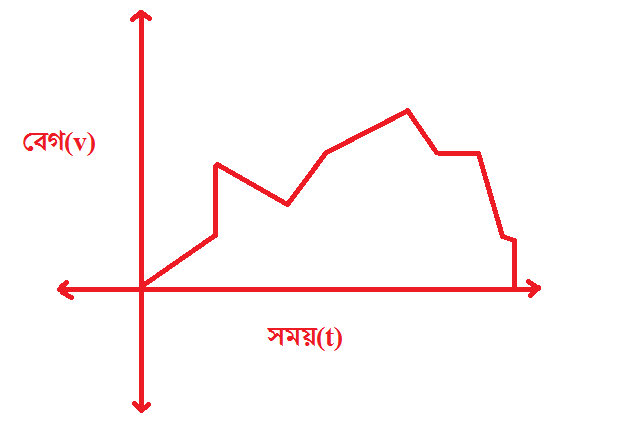
খুব সোজা সাপটা আবদার,সময় বনাম বেগের এই গ্রাফ থেকে আমাকে বলতে হবে,গাড়িটির অতিক্রান্ত দূরত্ব কত? আচ্ছা,আজকে এর গাণিতিক উত্তর না দিলেও চলবে,কীভাবে এটাকে সল্ভ করা যায় এবং কেন আমাদের উত্তরটা সঠিক হতে পারে,তার পিছনের যুক্তিগুলো ক্লিয়ার করতে পারলেই হবে।
দেখো,একটি গাড়ি সমবেগে ১০ সেকেন্ড ২০মি/সে বেগে চলে গেলে,আমরা বলি গাড়িটি ২০০ মিটার অতিক্রম করে ফেলেছে। s=vt সূত্রটি সমবেগের ক্ষেত্রে খাটে। আমরা যখন বেগ বনাম সময় গ্রাফ আঁকি,তখন কিন্তু একটি অক্ষে সময় নিলে আরেকটি অক্ষে নিই বেগ। তার মানে,এই দুটো মাত্রাকে গুণ দিয়ে এদের কেবলমাত্র মান টাকেই আমরা বলে ফেলি অতিক্রান্ত দূরত্ব,রাইট? ( সমবেগের ক্ষেত্রে )
খেয়াল করে দেখো,একটা আয়তক্ষেত্রের ভূমি এবং প্রস্ত দেয়া থাকলে এদেরকে গুন দিলে আমরা এর ক্ষেত্রফল পেয়ে যাই। এখানে একই জিনিস কাজ করছে। বেগ এবং সময়কে আমরা যদি দুটো আলাদা মাত্রা ধরি,তাহলে তাদেরকে গুন দিলে আমরা একটি ক্ষেত্রফল অবশ্যই পাবো,যার মান নির্দেশ করবে অতিক্রান্ত দূরত্ব! 😀
তার মানে আমাদের উপরের সমস্যাটার ক্ষেত্রে এই আঁকাবাঁকা যেই ছবিটা দেখা যাচ্ছে,তার ক্ষেত্রফলটা যেকোনোভাবে বের করতে পারলেই তোমরা বলে দিতে পারবে অতিক্রান্ত দূরত্বটা কত হবে! 😀
কিছু প্রশ্ন এবং উত্তরঃ
১)
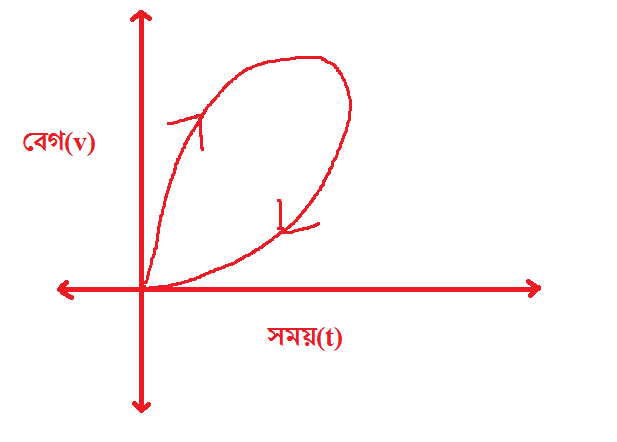
ভাইয়া,এখানে গাড়ি কর্তৃক অতিক্রান্ত দূরত্ব কত?
উত্তরঃ প্রশ্ন সঠিক নয় ভাইয়া। তোমার এই গ্রাফটাকে অবশ্যই আগে একটা ফাংশন হতে হবে,না হয় ফ্রেমটা ইনভ্যালিড হয়ে যাবে। তুমিই বলো,একটা গাড়ি একই সময়ে কীভাবে দুটো বেগ ধারণ করতে পারে? 🙂
২) আমি যদি একটি বিল্ডিং এর ছাদে উঠে আনুভূমিকভাবে বিভিন্ন বেগে অনেকগুলো বল ছুড়ে মারি,তাহলে তারা কত সময় পরে ভূমিতে পড়বে?
উত্তরঃ একই সময়ে পড়বে। কেন পড়বে,চিন্তা করো। না পারলে আরো চিন্তা করো।
৩)
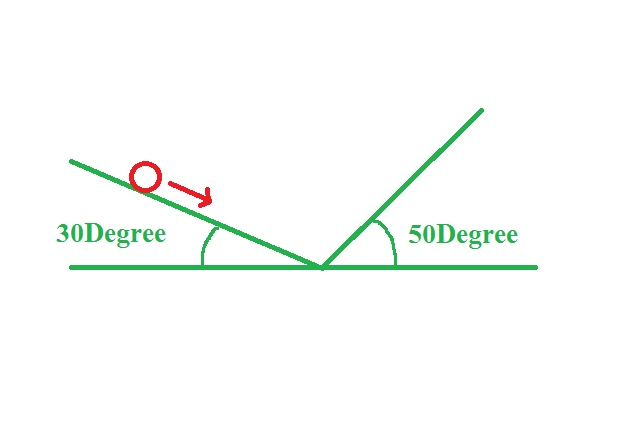
বলটি ভূমি থেকে ২ মিটার উঁচুতে আছে ধরুন। বলটি গড়িয়ে গড়িয়ে পাশের বাঁধটি অতিক্রম করে কতটুক উঠে যেতে পারবে?
উত্তরঃ ২ মিটারই উঠতে পারবে! শক্তির সংরক্ষণশীলতার নীতি। আগামী পর্বে এইটার উত্তরটা ব্যাখ্যা করবো। জাফর স্যারের বইতে এই সমস্যাটা আছে। 🙂
আজকে এটুকুই। আগামীতে আরো ভালো কিছু নিয়ে আসার চেষ্টা থাকবে। সে পর্যন্ত আমাদের সাথেই থাকো। ভালো থাকো।

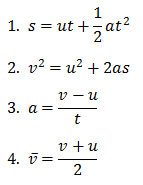

ভাল ছিল 😀 সামনে আরো রেগুলার আমাদের জন্য পোস্ট দেবার চেষ্টা করবেন ভাইয়া 😛
জন্ডিস টা কাটিয়ে উঠেই রেগুলার হবো ভাইয়া,দোয়া করবেন। :’)
khubi valo laglo bhaia 🙂
Khobi valo
Awesome chilo vaia…. Erokom post aro niye asben please..