প্রাইম প্রাইম প্রাইম!! সংখ্যার মধ্যে এই প্রাইম নাম্বার নামক ব্যাপারটা আমার সবচেয়ে প্রিয়! সবকিছুতেই প্রাইম খুঁজে পেতে ভালো লাগে – সেটা ব্যক্তিগত জীবন থেকে রাজনৈতিক জীবন,কোনো ক্ষেত্রেই বাদ যায়না। :p
প্রাইম বা মৌলিক সংখ্যা বলতে আমরা বুঝি কি আসলে- যে সংখ্যাটাকে ”১ এবং ঐ সংখ্যাটা” বাদে আর অন্য কোনো কিছু দিয়ে ”নিঃশেষে” বিভাজন করা যায়না!
যেমন ধরোঃ ৭। তুমি একে চাইলে ১ দিয়ে নিঃশেষে ভাগ করে দিতে পারো,কিংবা ৭ দিয়েও কাজটা চালাতে পারো। প্রথম ক্ষেত্রে ভাগফল পাবে ৭ , আর এরপরের কেইসে পাবে ১। তুমি ২ দিয়ে ভাগ করলে আবার ১ ভাগশেষ থেকে যাবে,আমাদের শর্তই হচ্ছে আর যাই থাক,”কোনো ভাগশেষ থাকা যাবে না!” 8|
***** ১ কিন্তু প্রাইম নাম্বার নয়!! ২ হচ্ছে একমাত্র প্রাইম নাম্বার,যে জোড়*****
খুব সহজ ব্যাপার,আমরা তাহলে একটা নাম্বার প্রাইম হতে পারে কিনা,সেটা যাচাই করার জন্য একটা কোড লিখে ফেলি! 😀 কোডটা কাজ করবে এভাবেঃ
১) প্রথমে একটা নাম্বার ইনপুট নিবে।
২) এরপর ২ থেকে ( কেন ২ থেকে? ১ থেকে কেন না? 😮 তোমরাই ভাবো! ) সেই সংখ্যাটার আগ পর্যন্ত একটি লুপ চালিয়ে চেক করে যাবে,এমন কোনো সংখ্যা আছে কিনা যেটা দিয়ে প্রদত্ত সংখ্যাটিকে নিঃশেষে ভাগ করা যায়।
৩) যদি অন্তঃত পক্ষে একটা নাম্বার দিয়েও ভাগ করা যায় ,তাহলে ওখানেই প্রোগ্রাম থামিয়ে দিয়ে বলে দিবো যে ”খামোশ! এই নাম্বারটি প্রাইম নয়! 8| ”
৪) আর যদি একটি নাম্বার দিয়েও ভাগ না যায়,তাহলে বলবো ” এটাই সেই প্রাইম নাম্বার! 😀 ”
৫) মাথায় রাখতে হবে,লুপ দিয়ে চেক করার সময় আমরা ”১ এবং সেই সংখ্যাটা” দুইজনকেই চেকিং থেকে বাদ রাখবো। কেন না,প্রাইম নাম্বার হলেও একটি নাম্বার ১ এবং সেই নাম্বারটি দিয়েও নিঃশেষে বিভাজিত হয়। 🙂 ( আয়হায়,বলেই দিলাম! )
কোডঃ
#include <stdio.h>
int main()
{
long long int i,n,temp=0;
scanf("%lld",&n);
for(i=2; i<n; i++)
{
if(n%i==0)
{
temp=1;
break;
}
}
if(n==0||n==1) temp=1;
if(temp==1) printf("Khamosh! Ei number ti Prime noy! -_- \n");
if(temp==0) printf("Ei shei Prime Number! ^_^\n");
return 0;
}
আমরা তাহলে এই কোডটি থেকে খুব সহজেই একটা সংখ্যা প্রাইম কিনা,সেটা বের করে ফেলতে পারবো। আচ্ছা,আমাদের এই প্রসেসটি খুবই বাজে একটা প্রসেস! আমরা আসলে এর চাইতে প্রায় ”বর্গমূল কম সময়ে” এই কাজটি করে ফেলতে পারতাম একটু খানি নাম্বার থিওরি জানলেই! 🙁 আমি জানি,তোমরা এই সূত্রটা জানোঃ
” একটি সংখ্যার বিভাজকগুলো জোড়ায় জোড়ায় অবস্থান করে। ধরি,একটি সংখ্যা যদি হয় P , তাহলে এর এমন দুইটি বিভাজক a এবং b অবশ্যই থাকবে যেন P=a*b হয় “
যেমনঃ তুমি জানোই যে ৮ এর একটি বিভাজক হচ্ছে ২। এখন উপরের সূত্র ব্যবহার করে আমরা কিন্তু ৮ এর আরেকটি বিভাজক খুব সুন্দরভাবেই বের করে ফেলতে পারি,সেটা হবে ৮/২ = ৪ । আরেকটা সংখ্যা নিই। উম,ধরো নিলাম এবার ৩২। ৩২ এর বিভাজকগুলোর দিকে যদি তাকাইঃ
৩২ এর বিভাজক সমূহঃ ১,২,৪,৮,১৬,৩২
এদেরকে এবার P=a*b এই সূত্রের আলোকে a আর b একত্রে নিয়ে জোড়ায় জোড়ায় সাজিয়ে ফেলিঃ
৩২ এর বিভাজক সমূহঃ (১,৩২),(২,১৬),(৪,৮)
তার মানে,আমরা যদি ৩২ এর ৩টি বিভাজক ১,২ এবং ৪ বের করে ফেলতে পারি,তাহলেই কিন্তু আমরা বলে দিতে পারছি যে ৩২ এর আসলে কতগুলো বিভাজক রয়েছে! ৪ যখন বের করেছি,আমরা কিন্তু আরেকটি উৎপাদক ৮ পেয়েই গেলাম,দেখো উপরে।
তাহলে প্রশ্ন এখন যেটা সেটা হচ্ছে,একটা নাম্বার প্রাইম কিনা সেটা জানতে হলে আমরা আসলে কতো পর্যন্ত চেক করে যাবো? এর উত্তরটা হচ্ছে ”sqrt(সংখ্যা) পর্যন্ত”। একটি নাম্বার যদি প্রাইম না হয়,তাহলে এর অর্ধেক সংখ্যক উৎপাদক sqrt(সংখ্যা) এই রেঞ্জের ভিতরেই অবস্থান করবে। আর বাকি অর্ধেক পাবো b=P/a এই সূত্রের সাহায্যে! 😀
মনে রাখবে,সকল সংখ্যার উৎপাদকের সংখ্যা জোড় সংখ্যাক,কেবল মাত্র বর্গ সংখ্যা ছাড়া। বর্গ সংখ্যার ক্ষেত্রে একটি জোড়াতে দুইটি একই সংখ্যা অবস্থান করে। যেমন ধরো,১৬ একটি বর্গ সংখ্যা। অতএব,একে বর্গমূল করলে তুমি পাচ্ছো ৪। তাই, ৪*৪=১৬ 🙂
তাহলে,এই লজিক দিয়ে আমরা কোডটাকে আরো এফিশিয়েন্ট করে দিতেই পারি!
কোডঃ
#include <stdio.h>
int main()
{
long long int i,n,temp=0;
scanf("%lld",&n);
for(i=2; i*i<=n; i++)
{
if(n%i==0)
{
temp=1;
break;
}
}
if(n==0||n==1) temp=1;
if(temp==1) printf("Khamosh! Ei number ti Prime noy! -_- \n");
if(temp==0) printf("Ei shei Prime Number! ^_^\n");
return 0;
}
চমৎকার! একটুখানি নাম্বার থিওরি আমাদের কোডটাকে কতটুক দ্রুত করে দিয়েছে দেখতে চাও? ১০০০০২৫২৬১ এই সংখ্যাটি একটি প্রাইম নাম্বার। তুমি এই সংখ্যাটি প্রাইম কিনা সেটা প্রথম কোডটাকে চেক করতে দাও,এবং তারপরে সেটা দ্বিতীয় কোডটাকে চেক করতে দাও। সময়ের পার্থক্য দেখে মজা না পেলে,মূল্য ফেরত।
ডাবল মজা পেতে চাইলে,৩৪৪৪৫৩৩৩৩৪৩৪৩৭ এই নাম্বারটি দিয়ে দেখো। :p
এবার তোমাদের আরেকটু কঠিন কাজ দিতে চাই। ধরো,আমি তোমার সামনে বসে আছি। তোমাকে আমি ১ সেকেন্ড এর মতো টাইম দিলাম,তুমি এই সময়ের মাঝে ১ থেকে ১০০০০০০০ (সাতটা শূন্য ) এর মধ্যে যতগুলো প্রাইম নাম্বার আছে,সব জেনারেট করে রেখে দিবা। আমি তোমাকে এর পর এই রেঞ্জের মধ্যে জিজ্ঞেস করতে শুরু করবো, ” এই ছেলে , বলো উমুক প্রাইম কিনা,তুমুক প্রাইম কিনা!” তখন তুমি তৎক্ষণাৎ উত্তর দিয়ে দিবে , নাম্বারটা প্রাইম,নাকি কম্পোজিট। পারবে?
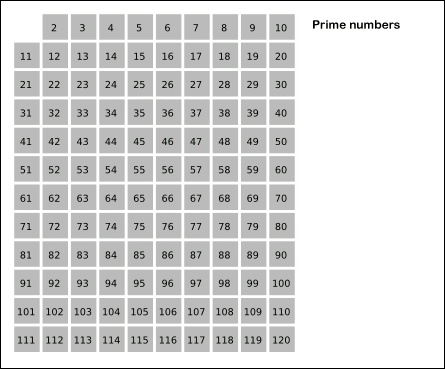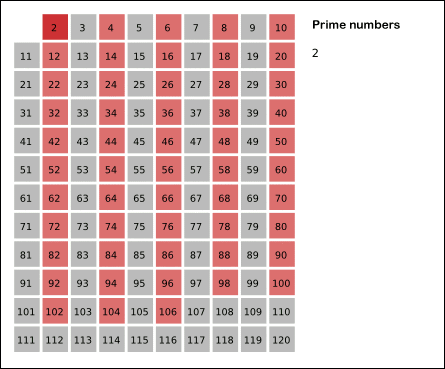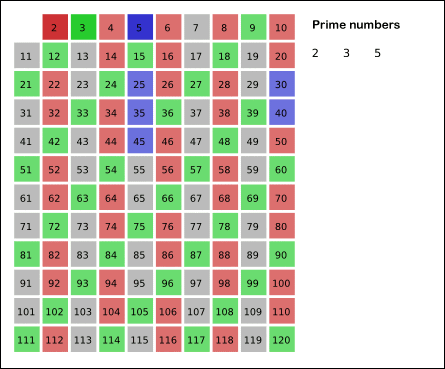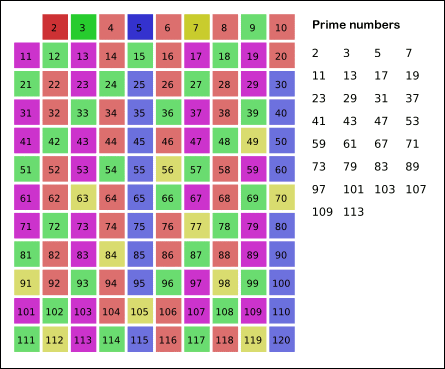
এরজন্য আমরা এখন যেই অ্যালগরিদমটি ব্যবহার করবো,তাকে বলা হয় Sieve of Eratosthenes. 🙂 উদাহরণ যদি দিই, প্রথমে আমরা ১ থেকে ২৫ পর্যন্ত সবগুলা নাম্বার একটা বক্সে লিখে ফেলবো। এরপর ১ কে আগেই বাদ দিবো,কারণ আমরা আগেই জানি ১ প্রাইম নাম্বার নয়। ২ থেকে শুরু করবো। ২ এর যতগুলো গুণিতক রয়েছে,আমরা এবার সবাইকে কেটে দিবো একটা ক্রস দিয়ে,কারণ এরা কেউই প্রাইম নাম্বার হতে পারেনা। ২ কে কিন্তু কাটবো না,যাকে দিয়ে শুরু করবো,সে থেকে যাবে। :’) এর পর ধরবো ৩ কে। একে না কেটে,এর সব গুণিতক গুলো কে কেটে দিবো। এরপর এভাবে আগাতে থাকবো। খুব শীঘ্রই দেখা যাবে যে,আমরা ১ থেকে ২৫ পর্যন্ত যতগুলো প্রাইম নাম্বার আছে,তাদের বের করে ফেলতে পেরেছি। আমি তোমাদের এই ব্যাপারটি একটা এনিমেশনের মাধ্যমে বুঝানোর চেষ্টা করি।
দেখো,আমরা কিন্তু বিভাজকের সমস্ত সূত্র মনের অজান্তেই চমৎকার ভাবে আঁকিবুঁকি করতে করতে এপ্লাই করে মস্ত বড় কাজটা করে ফেলেছি! এবার মনোযোগ দাও,আমি তোমাকে প্রশ্ন করার আগে যেই ১ সেকেন্ড সময় দিয়েছিলাম,এর মাঝে তুমি ১ থেকে ১০০০০০০০ এর মধ্যে সিভ এপ্লাই করবে। তারপর আমি প্রশ্ন করলে শুধু দেখে দেখে উত্তর দিয়ে দিবে। 😀
আমরা যেভাবে সিভ এর কোডটি লিখতে পারিঃ
১) প্রথমে গ্লোবালি একটা Array ডিক্লেয়ার করবো,এবং এর সাইজ দিবো 9999999। জেনে থাকার কথা,গ্লোবালি কিছু ডিক্লেয়ার করলে,তার ভিতর ০ এসাইন হয়ে থাকে।
২) আমরা এবার লুপ চালাবো কিছু শর্ত অনুযায়ী। যদি নাম্বারটি প্রাইম হয়,তাহলে সেই ইন্ডেক্সের নাম্বারটিতে ০ ই রাখবো,আর যদি প্রাইম না হয়,তাহলে সেখানে ১ রেখে দিবো।
৩) কোড নিয়ে কিছু কথা বলি। আমি ২ থেকে চেক করা শুরু করেছি। কারণ তোমরা জানোই, ২ এর চাইতে ছোট কোনো প্রাইম নাম্বার নেই। শুণ্য এবং এক যে প্রাইম নয়,তাই আমি আগেই তাদের কে ১ দিয়ে অ্যাসাইন করে রেখেছি। ( যতভাবে প্রোগ্রাম এর কাজ কমানো যায় আর কি)
৪) আমরা প্রতিটি নাম্বার চেক করিনি,২টা নাম্বার পরপর চেক করেছি। আমরা চেকিং এর সময় জোড় সংখ্যাগুলোকে বাদ দিয়ে দিয়েছি।
৫) কোডের শুরুতেই সকল জোড় সংখ্যা যে প্রাইম নয়,সেই জ্ঞান খাটিয়ে তাদেরকে আগেই বাদ দিয়ে দিয়েছি। 8|
#include <stdio.h>
#include <math.h>
int a[9999999];
int main()
{
int i,j,n,N=9999999;
int sq=sqrt(N);
a[0]=1;
a[1]=1;
for(i=4; i<N; i=i+2) a[i]=1; // 2 theke shuru korini,karon 2 ebong 3 prime number,sheta amra aagei jani
for(i=3; i<=sq; i=i+2)
{
if(a[i]==0)
{
for(j=i*i; j<=N; j+=i) a[j]=1;
}
}
scanf("%d",&n);
if(a[n]==0) printf("Prime\n");
else printf("Not Prime\n");
return 0;
}
পরবর্তী পর্বে আমরা মেমরী সাশ্রয়ী বিটওয়াইজ সিভ নিয়ে গপ্পো করবো। আজ এই পর্যন্তই!
জিজ্ঞাসা থাকলে কমেন্ট বক্স খোলা-ই আছে! হ্যাপি কোডিং!


chorom to 😀
🙂 Thanks
onek helpful akta tutorial 🙂 number theory er upor aro tutorial chai 😀
চমৎকার 🙂
লেখার স্টাইল অস্থির । লেখা টি খুব ভালো লাগলো ।
if condition ta use na korlew tw hoy mne hoy,,,tai na vaia?? r ami 10000000/10000001/10000002 input dilew tw ‘PRIME’ dkhacche !! eta kno hocche !! ektu explain korle vlw hoy vaia …
Mahee Mashrur
এখানে আমাদের সংখ্যার রেঞ্জটা কত নেয়া হয়েছে,একটু চিন্তা করে দেখো তো! 😀 আশা করি উত্তর পেয়ে যাবে,কেন এমনটা হচ্ছে। এটা মাথায় রাখলে ভালো,১ থেকে N পর্যন্ত স্বাভাবিক সংখ্যার মধ্যে মোটামুটি অর্ধেকের চাইতে কম সংখ্যা হচ্ছে প্রাইম সংখ্যা। তুমি মোটামুটি আরেকটূ বড় রেঞ্জের জন্য সিভ লিখতে গেলে,এভাবে আরেকটা অ্যারে নিয়ে সেটাকে অপ্টিমাইজ করে ব্যবহার করে দেখতে পারো।
আর if condition ইউজ না করলে হবে না। তুমি তাহলে তোমার গিভেন রেঞ্জের বর্গমূলের মধ্যে সমস্ত সংখ্যাকে জোড় আর বিজোড় বানায় দিচ্ছো। এছাড়া আর কিছুই হবেনা।
Mahee Mashrur
হিন্ট দিয়ে দিই, আমি যে উপরে অ্যারের সাইজ 9999999 দিয়েছি,তুমি সেটাকে 50000000 দিয়ে পরিবর্তন করে দাও। সাথে N=50000000 দিয়ে দাও। এবার দেখো।