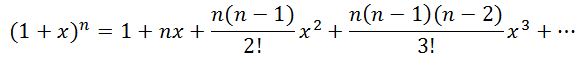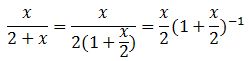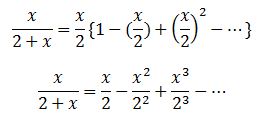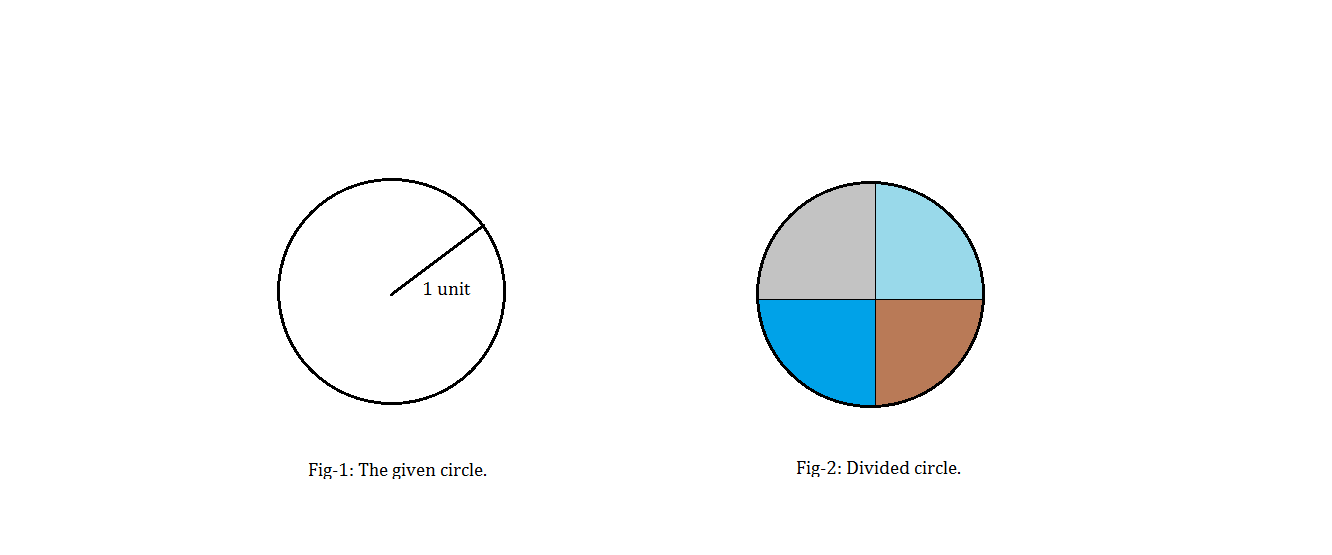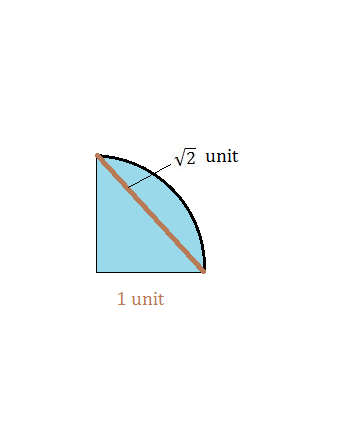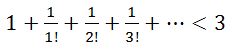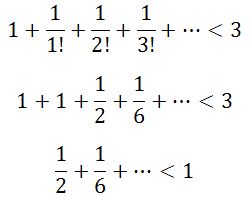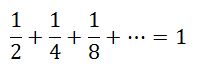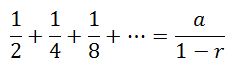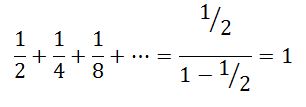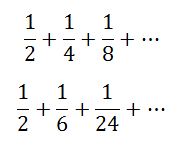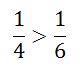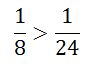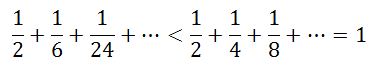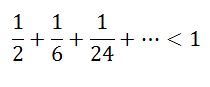সমস্যা-1: ![]() কে x এর বহুপদী আকারে প্রকাশ কর।
কে x এর বহুপদী আকারে প্রকাশ কর।
সমাধান: এই সমস্যার সমাধানের জন্য আমাদেরকে দ্বিপদী উপপাদ্যের সাহায্য নিতে হবে। এই উপপাদ্য অনুসারে,
সমস্যায় প্রদত্ত রাশিটিকে আমাদের একটু ঘুরিয়ে লেখতে হবে আরকি!
এখন দ্বিপদী উপপাদ্যের সাহায্যে বিস্তৃত করলে পাব,
সমস্যা-2: 1 একক ব্যাসার্ধের একটি বৃত্তের পরিধি অথবা এর অভ্যন্তরীন যেকোনো জায়গা হতে 5 টি বাছা হল। দেখাও যে, বাছাইকৃত 5 টি বিন্দুর মধ্য থেকে এমন 2 টি বিন্দু পাওয়া যাবে যাদের সর্বোচ্চ দূরত্ব ![]() একক।
একক।
সমাধান: প্রথমেই একটি অতীব সাধারণ কিন্তু, অকল্পনীয় ক্ষমতাসম্পন্ন ‘নীতি’ শিখব আমরা। ধরা যাক, তোমার কাছে 4 টি কবুতরের খোপ আছে। তবে, তুমি বাজার থেকে 5 টি কবুতর কিনে নিয়ে এসেছ। এখন, তুমি যদি সবগুলো কবুতরের জন্য জায়গা করে দিতে চাও তাহলে নিশ্চয়ই কোনো একটি খোপে দুটো কবুতর আটাতে হবে! এই সাধারণ ব্যাপারটাকেই বলে Pigeonhole Principle । (এর বাংলা কোনো নাম জানা নেই আমার) তাহলে, এখন Pigeonhole Principle টা এক লাইনে লিখে ফেলি!
“যদি কবুতরের খোপের (pigeonhole) এর চেয়ে কবুতরের (pigeon) সংখ্যা বেশি হয় এবং কবুতরগুলোকে ঐ খোপগুলোতে আটানোর চেষ্টা করা হয়, তাহলে কমপক্ষে একটি খোপে ন্যূনতম দুটি কবুতরকে রাখতে হবে।”
অনেকেই হয়তো ভাবছ, কি এমন আহামরি ‘নীতি’! আসলে, কোনো নীতিই আহামরি কিছু না। তবে, আমরা মানুষ তো, তাই সাধারণ কিছু দিয়েই অসসাধারণ কিছু করে ফেলতে পারি!
1 একক ব্যাসার্ধের ঐ বৃত্তটিকে এখন আমরা প্রতিসম চারটি অংশে ভাগ করব।
সমস্যায় বলা হয়েছে যে, 5 টি বিন্দু বাছা হয়েছে এই বৃত্তটি থেকে। বৃত্তটিতে চতুর্থাংশ আছে 4 টি। এখন এই চতুর্থাংশগুলোকে কবুতরের খোপ আর বিন্দুগুলোকে কবুতর হিসেবে চিন্তা কর। কবুতর আছে বেশি। তাই যেকোনো একটি খোপে দুইটি কবুতর তো আটাতে হবেই!
অর্থাৎ, আমরা এমন দুটি বিন্দু অবশ্যই পাব যারা একই চতুর্থাংশতে অবস্থিত হবে। আচ্ছা, এরকম একটি চতুর্থাংশে অবস্থিত দুটি বিন্দুর সর্বোচ্চ দূরত্ব কত হতে পারে? একক। কিছু কাবজাব করতে হবে কঠোরভাবে প্রমাণের জন্য! কিন্তু, আমি প্রমাণ ব্যতিরেকেই বলে দিলাম।
আরো কিছু কি প্রমানের বাকি আছ? 😀 আশা করি, Pigeonhole Principle এর গুরুত্ব বুঝতে পেরেছ। [ভবিষ্যতে এই উপপাদ্য নিয়ে আলাদা করে লিখার ইচ্ছা আছে!:) ]
সমাধান: প্রদত্ত সমীকরণটিকে আরেকটু সংক্ষিপ্ত করার চেষ্টা করি।
মানে, আমাদের দেখাতে হবে যে, 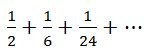 এই সিরিজটার যোগফল 1 এর চেয়ে কম হবে!
এই সিরিজটার যোগফল 1 এর চেয়ে কম হবে!
এই উক্তিটি আমরা একটু ভিন্নভাবে প্রমাণ করব।
ধর, তোমার কাছে একটি কুমড়া আছে। তুমি সিদ্ধান্ত নিলে যে এটি তুমি তোমার অসীম(!) সংখ্যক বন্ধুদের মাঝে ভাগ করে দিবে। কিভাবে এটি করা যায়? একটা উপায় আছে! প্রথম যে বন্ধু আসবে তাকে তুমিও অর্ধেকটা কুমড়া দিবে। তারপরের জনকে বাকি অর্ধেকের অর্ধেক অংশ দিবে। মোদ্দা কথা হল, তোমার কাছে কোনো বন্ধু আসলেই তুমি তাকে তোমার আয়ত্ত্বে থাকা কুমড়ার অংশ থেকে অর্ধেক দিবে। এটাকে আমরা গণিতের ভাষায় এভাবে লিখি,
[কুমড়া থিওরির ক্রেডিট: তারিক আদনান মুন ভাই]
যারা কাঠখোট্টা প্রমাণ চাও তাদের জন্য নিচের লাইনগুলো লিখলাম,
[a=প্রথম পদ; r=সাধারণ অনুপাত]
(see geometric series)
এখন আমাদের কাছে দুটি অসীম ধারা আছে। নিচে এদের আবার লিখছি,
দুটো ধারারই প্রথম পদ সমান। এরপরের পদগুলোতে গরমিল শুরু হয়েছে।
যেমন,
কারণ,
একইভাবে,
তারমানে, 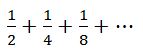 এই ধারাটির মান
এই ধারাটির মান 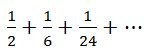 ধারাটির চেয়ে বেশি!
ধারাটির চেয়ে বেশি!
বা,
ব্যাস, হয়ে গেল প্রমাণ!