ইতঃপূর্বে তোমরা ধারাবাহিকভাবে সরল ছন্দিত স্পন্দন সম্পর্কে জেনেছিলে। আজ আমরা কিছু সমস্যা ও তার সমাধানের মাধ্যমে ব্যাপারটাকে আরেকটু কাছ থেকে দেখবো। 🙂
আচ্ছা, একটু সরল ছন্দিত স্পন্দনের ধারণাটাকে পুনরালোচনা করা যাক।(এখন থেকে লেখার শেষ পর্যন্ত আমরা “সরল ছন্দিত স্পন্দন” কে SHM বলে সম্বোধন করব।) আমরা জানি, SHM এর একটি গুরুত্বপূর্ণ বৈশিষ্ট্য হল, এর যেকোন মুহূর্তের ত্বরণ তার সাম্যাবস্থা থেকে সরণের সমানুপাতিক এবং বিপরীতমুখী। অর্থাৎ, a ∝ -x অথবা আমরা আরেকটু এগিয়ে বলতে পারি, Fnet ∝ -x (প্রত্যয়নী বল সরণের সমানুপাতিক।) যেহেতু নিউটনের সূত্রানুসারে, F = ma.
যারা একটু বড় তারা হয়ত এতদিনে জেনে ফেলেছো, SHM এর differential equation হল, 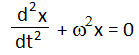 যেখানে, ω2 = k/m অর্থাৎ কোন বস্তুর গতি যদি এই সমীকরণ মেনে চলে তবে তাকে আমরা SHM বলব। কারণ এই সমীকরণ মেনে চললেই তা F ∝ -x বা a ∝ -x মেনে চলবে।
যেখানে, ω2 = k/m অর্থাৎ কোন বস্তুর গতি যদি এই সমীকরণ মেনে চলে তবে তাকে আমরা SHM বলব। কারণ এই সমীকরণ মেনে চললেই তা F ∝ -x বা a ∝ -x মেনে চলবে।
তাহলে আর কথা না বাড়িয়ে শুরু করা যাক।
প্রথমেই আমাদের পরিচিত সমস্যা দিয়ে শুরু করি।
সমস্যা ১: সরল দোলকের গতি:
ক্রিয়াশীল প্রত্যয়নী বল, F = – mg sinθ এখন, যদি খুব ক্ষুদ্র হয়(4o অপেক্ষা ছোট) তাহলে আমরা বলতে পারি, sinθ = θ (প্রায়) তাহলে, F = – mg θ ।এখন যেকোন মুহূর্তে সাম্যাবস্থা থেকে বস্তুর রৈখিক সরণ x হলে, x = L θ, তাহলে, F = – mg (x/L)
বা,![]()
বা,![]()
অর্থাৎ 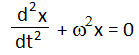 যেখানে ω2 = g/L.
যেখানে ω2 = g/L.
তার মানে, সরল দোলকের গতি একটি SHM.
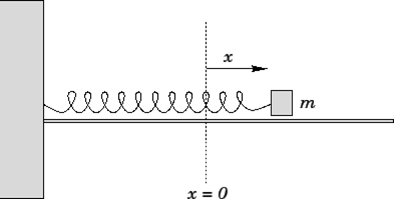
সমস্যা ২: নগণ্য ভরের স্প্রিং ও একটি বস্তুঃ
নগণ্য ভরের একটি স্প্রিং এর এক প্রান্তে m ভরের একটি বস্তু আর এক প্রান্ত দেয়ালের সাথে লাগানো। স্প্রিং ধ্রুবক k । এখন পুরো ব্যাবস্থাটাকে একটি ঘর্ষণহীন টেবিলের উপর রেখে বস্তুটিকে একটু টেনে ছেড়ে দিলে স্প্রিং এর যে গতি পাওয়া যাবে তা একটি SHM.
হুকের সূত্র থেকে আমরা জানি, স্প্রিং বল = ক্রিয়াশীল প্রত্যয়নী বল, F = – kx
বা,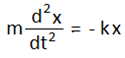
বা,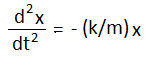
অর্থাৎ, 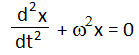 যেখানে, ω2 = k/m
যেখানে, ω2 = k/m
সুতরাং, স্প্রিং এর গতি একটি SHM.
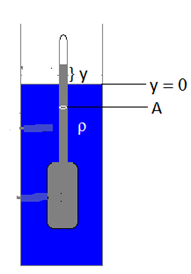
সমস্যা ৩: হাইড্রোমিটার :
একটি m ভরের ও A প্রস্থচ্ছেদের ক্ষেত্রফল বিশিষ্ট হাইড্রোমিটার ρ ঘনত্ববিশিষ্ট একটি তরলে আংশিক নিমজ্জিত আছে। হাইড্রোমিটারটিকে অল্প পরিমাণ উপরে তুলে ছেড়ে দিলে এটি দুলতে থাকে। এর গতি একটি SHM.
হাইড্রোমিটারটিকে y পরিমাণ উপরে তুলতে ক্রিয়াশীল প্রত্যয়নী বল = ঐ জায়গা থেকে অপসারিত তরলের ওজনের সমান।
অর্থাৎ F = -mg
বা, F = – Vρ g
বা, F = -Ayρ g
বা,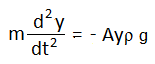
বা,![]() যেখানে, ω2 = (Agρ)/m
যেখানে, ω2 = (Agρ)/m
সুতরাং, এখানে হাইড্রোমিটারটির গতি একটি SHM.
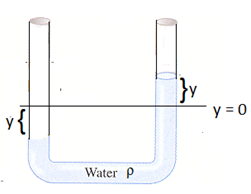
সমস্যা ৪: U -টিউবে পানিঃ
একটি U আকৃতির টিউবের L দৈর্ঘ্য পরিমাণ জায়গাজুড়ে কিছু পানি আছে সম্পূর্ণ পানির ভর m আর ঘনত্ব r যেকোনো এক নলের পানিকে কিছু পরিমাণ উপরে তুলে ছেড়ে দিলে টিউবের ভিতরের পানিস্তম্ভ দুলতে থাকে। পানির গতি একটি SHM.
এখানে, একটি নলের পানির স্তম্ভকে পরিমান উপরে তুলায় সম্পূর্ণ দৈর্ঘ্যের পানির স্তম্ভের পরিমাণ সরণ হয়। তাহলে সম্পূর্ণ পানির উপর ক্রিয়াশীল প্রত্যয়নী বল = 2y দৈর্ঘ্যের পানির স্তম্ভকে উপরে তুলতে প্রয়োজনীয় বল = 2y দৈর্ঘ্যের পানির স্তম্ভের পানির ওজন।
অর্থাৎ, F = -mg
বা, F = -A(2y)ρ g = -2Ayρg
বা,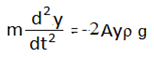
বা,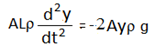
বা,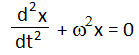 যেখানে, ω2 = (2Agρ)/(ALρ)= (2g/L)
যেখানে, ω2 = (2Agρ)/(ALρ)= (2g/L)
সুতরাং, পানির গতি একটি SHM.
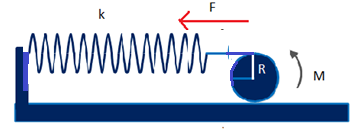
সমস্যা ৫: স্প্রিং ও ঘূর্ণনক্ষম সিলিন্ডারঃ
M ভর ও R ব্যাসার্ধের একটি সিলিন্ডার একটি স্প্রিং এর সাথে লাগানো, স্প্রিং ধ্রুবক k ।তাহলে সিলিন্ডারের গতি একটি SHM.
এখানে আমাদের ক্রিয়াশীল প্রত্যয়নী বলের কিছু অংশ সিলিন্ডারকে ঘুরাবে আর কিছু অংশ সিলিন্ডারকে সামনে পিছে আনা নেয়া করবে। ধরলাম, Fr অংশ সিলিন্ডারটিকে ঘুরায় আর Fx অংশ সিলিন্ডারটিকে সামনে পিছে দুলাতে থাকে। সিলিন্ডারটির নিজ অক্ষের সাপেক্ষে ঘূর্ণনজনিত টর্ক, τ যেহেতু R আর Fr এর মধ্যবর্তী কোণ 90o তাই
τ = RFr
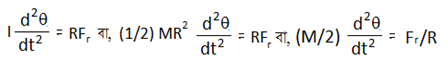
আবার x = Rθ
সুতরাং, ![]() অর্থাৎ,
অর্থাৎ, 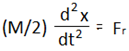 আবার,
আবার, 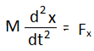 সুতরাং ক্রিয়াশীল মোট প্রত্যয়নী বল, F = Fx + Fr =
সুতরাং ক্রিয়াশীল মোট প্রত্যয়নী বল, F = Fx + Fr =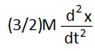
বা, F =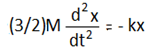
অর্থাৎ, 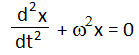 যেখানে, ω2 = (2k/3M)
যেখানে, ω2 = (2k/3M)
সুতরাং,সিলিন্ডারের গতি একটি SHM.
সমস্যা ৬: দুইটি নগণ্য ভরের স্প্রিং ও একটি বস্তুঃ
দুইটি নগণ্য ভরের স্প্রিং (স্প্রিং ধ্রুবক k1 , k2) এর এক প্রান্ত একটি দেয়ালের সাথে এবং অপর প্রান্ত একটি M ভরের বস্তুর সাথে (1)স্প্রিংদ্বয় সমান্তরালে (2)স্প্রিংদ্বয় সিরিজে সংযুক্ত। SHM এর differential equation টি নির্ণয় করতে হবে।
সমাধানঃ
(1) স্প্রিংদ্বয় সমান্তরালে
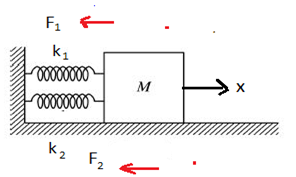
এখানে, ক্রিয়াশীল মোট প্রত্যয়নী বল = x পরিমাণ সরণে স্প্রিংদ্বয় দ্বারা প্রযুক্ত মোট বল.
F = – k1x – k2x
বা, 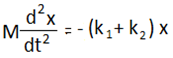
বা,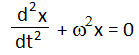 যেখানে, ω2 = (k1+k2)/M
যেখানে, ω2 = (k1+k2)/M
এখানে, উভয় স্প্রিং এর জন্যে ক্রিয়াশীল প্রত্যয়নী বল, F. (কারণ দুইটি স্প্রিং এর জন্যে আলাদা প্রত্যয়নী বল থাকলে স্প্রিং দুইটি বেঁকে যেত। যেহেতু স্প্রিং দুইটির একটিও বাঁকাচ্ছে না তাই উভয়ের জন্যে প্রত্যয়নী বল একই এবং তা মোট প্রত্যয়নী বলের সমান।) এখন ধরি, মোট সরণের কিছু অংশ x1 ১ম স্প্রিং আর কিছু অংশ x2 ২য় স্প্রিং এর প্রভাবে হয়।
F = -k1x1 = -k2x2 অর্থাৎ আমরা বলতে পারি, মোট সরণ x , k2:k1 অনুপাতে বিভক্ত হয়। ছোটবেলার ধারণা থেকে আমরা বলতে পারি,
x1 = {k2/(k1+k2)}x এবং x2 = {k1/(k1+k2)}x
অতএব, F = – {(k1k2)/(k1+k2)}x
বা,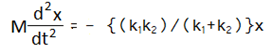
বা, 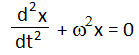 যেখানে, ω2 = {(k1k2)/(k1+k2)} /M
যেখানে, ω2 = {(k1k2)/(k1+k2)} /M
(উপরোক্ত ধারণা থেকে আমরা বলতে পারি, একাধিক স্প্রিং সমান্তরালে থাকলে তুল্য স্প্রিং ধ্রুবক হবে তাদের পৃথক পৃথক স্প্রিং ধ্রুবকের যোগফলের সমান। আর একাধিক স্প্রিং সিরিজে থাকলে তুল্য স্প্রিং ধ্রুবক হবে তাদের পৃথক পৃথক স্প্রিং ধ্রুবকের গুণবোধক বিপরীত রাশির যোগফলের বিপরীত রাশির সমান। মানে অনেকটা ধারক এর ধারকত্ব এর মত।)
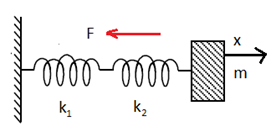
সমস্যা ৭: স্প্রিং এর মাঝে বস্তুঃ
দুইটি নগণ্য ভরের স্প্রিং (স্প্রিং ধ্রুবক k1 , k2) এর এক প্রান্ত একটি দেয়ালের সাথে এবং অপর প্রান্ত একটি M ভরের বস্তুর সাথে চিত্রের মত যুক্ত। SHM এর differential equation টি নির্ণয় করতে হবে।
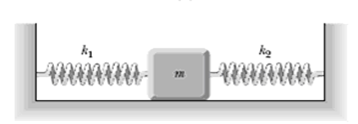
সমাধানঃ
এখানে, ক্রিয়াশীল মোট প্রত্যয়নী বল = x পরিমাণ সরণে স্প্রিংদ্বয় দ্বারা প্রযুক্ত মোট বল.
বা, F = – k1x – k2x (কারণ, প্রত্যয়নী বল দুইটির দিক একই।)
বা, 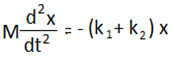
বা, 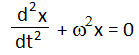 যেখানে, ω2 = (k1+k2)/M
যেখানে, ω2 = (k1+k2)/M
(কি কিছু মনে হচ্ছে? 😀 আসলে দেখো স্প্রিং দুইটি বস্তুটার সাথে সমান্তরালে যুক্ত আছে।)
সমস্যা ৮: উল্লম্বভাবে ঝুলন্ত স্প্রিং ও বস্তুঃ
নগণ্য ভরের একটি স্প্রিং এর এক প্রান্তে m ভরের একটি বস্তু আর এক প্রান্ত ছাদের সাথে নিচের চিত্রের মত লাগানো। স্প্রিং ধ্রুবক k । এই mass-spring system টার গতির সমীকরণ নির্ণয় করতে হবে।
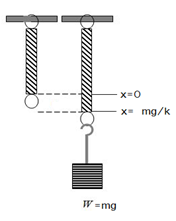
সমাধানঃ
ক্রিয়াশীল মোট প্রত্যয়নী বল, F = mg – kx
বা, 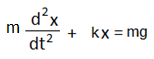
বা,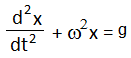 যেখানে, ω2 = k/m এটাই গতির সমীকরণ। এখন, আমরা জানি, সাম্যাবস্থান থেকে দোলন শুরু করলে, x(t) = A.sin(ωt+δ) কিন্তু উপরোক্ত সমীকরণের সাম্যাবস্থান mg/k পরিমাণ সরে গেছে। ফলে আগে আমরা কোন সময় t তে সরণের যে মান পেতাম এখানে তার থেকে mg/k পরিমাণ বেশি পাব। তাই আমাদের সরণের ফাংশন হবে, x(t) = A.sin(ωt+δ)+(mg/k)।
যেখানে, ω2 = k/m এটাই গতির সমীকরণ। এখন, আমরা জানি, সাম্যাবস্থান থেকে দোলন শুরু করলে, x(t) = A.sin(ωt+δ) কিন্তু উপরোক্ত সমীকরণের সাম্যাবস্থান mg/k পরিমাণ সরে গেছে। ফলে আগে আমরা কোন সময় t তে সরণের যে মান পেতাম এখানে তার থেকে mg/k পরিমাণ বেশি পাব। তাই আমাদের সরণের ফাংশন হবে, x(t) = A.sin(ωt+δ)+(mg/k)।
সমস্যা ৯:সমুদ্রে জাহাজঃ
একটি জাহাজের ভর m ও প্রস্থচ্ছেদের ক্ষেত্রফল A সমুদ্রের পানির ঘনত্ব ρw এখন, জাহাজটি পানিতে নামানোর সাথে সাথে এটি তার সাম্যাবস্থা থেকে অল্প পরিমাণ নিচে নেমে দুলতে থাকে, প্রমাণ করো জাহাজটির গতি একটি SHM এবং জাহাজটির কৌণিক কম্পাংক নির্ণয় করো।
সমাধানঃ
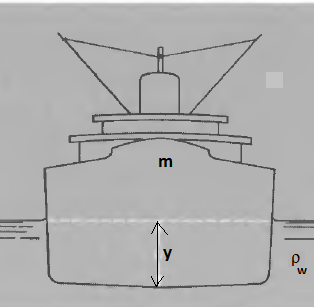
জাহাজটিকে y পরিমাণ নিচে নামাতে ক্রিয়াশীল প্রত্যয়নী বল = ঐ জায়গা থেকে অপসারিত তরলের ওজনের সমান।
অর্থাৎ F = -mg
বা, F = – Vρwg
বা, F = -Ayρwg
বা,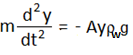
বা,![]() যেখানে, ω2 = (Agρw)/m
যেখানে, ω2 = (Agρw)/m
সুতরাং, এখানে জাহাজটির গতি একটি SHM এবং কৌণিক কম্পাংক ω = √ { (Agρw)/m}.
সমস্যা ১০: দুই বস্তু, এক স্প্রিংঃ
m1 ও m2 ভরের দুইটি বস্তু A ও B একটি স্প্রিং দ্বারা চিত্রের মত যুক্ত। স্প্রিং ধ্রুবক k ।এবার বস্তু দুইটিকে অল্প টেনে ছেড়ে দেয়া হল। বস্তু দুইটির গতির সমীকরণ নির্ণয় করো।
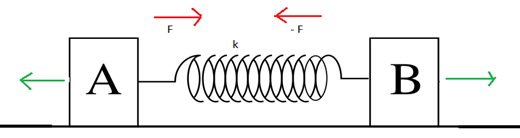
সমাধানঃ
ধরি, কোনো এক সময় ১ম বস্তুটি যখন তার সাম্যাবস্থা থেকে x1 পরিমাণ এবং ২য় বস্তুটির সরণ সাম্যাবস্থা থেকে x2 হয় তখন সিস্টেমের অবস্থা নিচের ছবির মত হয়।
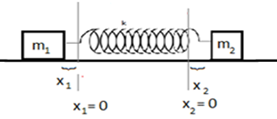
সুতরাং, (x1 + x2) পরিমাণ প্রসারণের জন্য ক্রিয়াশীল মোট প্রত্যয়নী বল (স্প্রিং বল), F = – k(x1 + x2) অর্থাৎ,
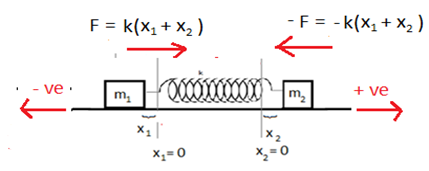 ।
।
(কারণ দুইটি বস্তুর দ্বারা ভিন্ন ভিন্ন প্রসারণের জন্য বস্তু দুইটির উপর ভিন্ন ভিন্ন বল প্রয়োগ করলে স্প্রিংটি বাঁকিয়ে যাওয়ার কথা যেহেতু স্প্রিংটি বাঁকিয়ে যাচ্ছে না তার মানে স্প্রিংটি দুইটি বস্তুর উপর সমান মানের বল প্রয়োগ করছে । আসলে ব্যাপারটা বস্তু দুইটির পারসস্পরিক interaction এর ফল যেখানে স্প্রিংটি বস্তুদ্বয়ের সংযোগ মাধ্যম হিসেবে কাজ করছে।)
দুইটি বস্তুর গতিই SHM. এর আগে সাধারণ ক্ষেত্রে আমাদের একটি বস্তু ছিল স্থির (দেয়াল) আর আরেকটি গতিশীল। আমরা এখানেও আমাদের এই two body system টাকে একটি চিত্রের মত single body system হিসেবে বিবেচনা করব যেখানে ক্রিয়াশীল বল একই থাকবে অর্থাৎ F
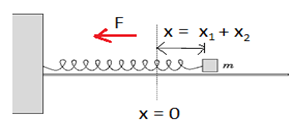
এবং স্প্রিং ও একই থাকবে মানে স্প্রিং ধ্রুবক k এবং স্প্রিং এর প্রসারণ (x1 + x2) = x হবে। অর্থাৎ সহজ কথায় আমরা আমাদের একটি বস্তু A এর উপর একজন পর্যবেক্ষক বসিয়ে দিব এবং ধরি, পর্যবেক্ষক জানে স্প্রিংটি F বল প্রয়োগ করছে m2 ভরের বস্তুটির উপর। তাহলে ঐ পর্যবেক্ষক (সে কেবল m2 কে গতিশীল দেখবে) যা দেখবে তাই হবে system এর গতি । (পর্যবেক্ষক দেখবে ঐ মুহূর্তে স্প্রিংটি (x1 + x2) পরিমাণ প্রসারিত হচ্ছে)।
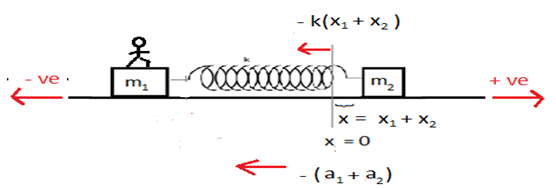
অর্থাৎ আমরা এখানে আমাদের আপেক্ষিক গতির ব্যাপারটাকে কাজে লাগাব। ধরি, A বস্তুটি a1 ত্বরণে এবং B বস্তুটি a2 ত্বরণে গতিশীল তাহলে A বস্তুর পর্যবেক্ষকের সাপেক্ষে B বস্তুর ত্বরণ -(a1 + a2), ত্বরণের মান (a1 + a2), যেহেতু একই পরিমাণ বলে (F) ত্বরণ বেশি হচ্ছে তাই পর্যবেক্ষক এর কাছে m2 বস্তুটির ভর কমে গেছে বলে মনে হবে অর্থাৎ আমাদের single body system এর বস্তুর ভর কম হবে। ধরি, পর্যবেক্ষক এর কাছে m2 বস্তুটির ভর μ বলে মনে হচ্ছে তাহলে তার কাছে বলের মান, F = μ(a1 + a2)। (এখন আমরা শুধুমাত্র মান বিবেচনা করব কারণ বল যেদিকে ক্রিয়া করে ত্বরণও সেদিকে ক্রিয়া করে ) তাহলে, F = m1a1 = k(x1 + x2)
বা, a1 = k(x1 + x2)/m1
আবার, a2 = k(x1 + x2)/m2
অর্থাৎ, (a1 + a2) = k(x1 + x2){(1/m1)+ (1/m2)}
বা, {(1/m1)+ (1/m2)}-1 (a1 + a2) = k(x1 + x2) = F = μ(a1 + a2)
অর্থাৎ , μ = {(1/m1)+ (1/m2)}-1
বা, μ = m1m2/(m1 + m2)
বা,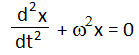 যেখানে, ω2 = k/μ এবং μ = m1m2/(m1 + m2) এটাই গতির সমীকরণ।
যেখানে, ω2 = k/μ এবং μ = m1m2/(m1 + m2) এটাই গতির সমীকরণ।
এই μ কে বলা হয় reduced mass কারণ μ < m1 , μ < m2 .
সমস্যা ১১: চার্জ এবং SHM:
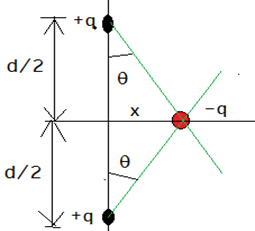
+q চার্জবিশিষ্ট দুইটি বিন্দু চার্জ শুন্যে পরস্পর d দুরত্বে অবস্থিত। এদের থেকে x দুরত্বে চিত্রের মত –q চার্জবিশিষ্ট একটি বিন্দু চার্জ অবস্থিত। যদি x এর থেকে d অনেক বড় হয় অথবা θ যদি খুব ক্ষুদ্র হয় তাহলে চার্জের গতি একটি SHM.
সমাধানঃ
ক্রিয়াশীল মোট প্রত্যয়নী বল, F = 2Fccos θ কারণ কুলম্ব বলের সাইন উপাংশগুলো পরস্পর নিষ্ক্রিয় হয়ে যায়।
বা, F = -(1/2πεo){q2/(x2+(d/2)2)}cosθ
এখানে, cosθ = {x / √(x2+(d/2)2)}
অর্থাৎ, F = -(1/2πεo){(q2x)/(x2+(d/2)2)3/2}
এখন, x এর থেকে d অনেক বড় অথবা θ যদি খুব ক্ষুদ্র বলে,
F = -(1/2πεo){(q2x)/(d/2)3}
বা, F = -(4/πεo){(q2x)/d3}
বা, F = – {(4q2)/(πεod3)} x
বা, 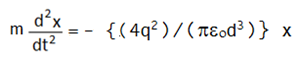
বা,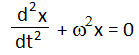 যেখানে, ω2 = {(4q2)/(mπεod3)}
যেখানে, ω2 = {(4q2)/(mπεod3)}
তাহলে এক্ষেত্রে – q চার্জের গতি একটি SHM.
সমস্যা ১২: আস্ত বস্তুই যখন দোলকঃ
একটি বস্তু এর একটি শীর্ষ থেকে ঝুলানো আছে। এর গতির সমীকরণ বের করতে হবে।
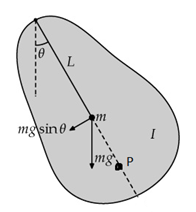
সমাধানঃ এখন যেহেতু বস্তুটি তার ঝুলন বিন্দু দিয়ে অতিক্রমকারী রেখার (মনিটর বরাবর বাইরের দিকে। 😀 ) সাপেক্ষে ঘুরার উপক্রম হয় তাই আমরা বলতে পারি,
প্রত্যয়নী টর্ক, τ = – (mgsinθ)L
(কারণ বস্তুর ওজন অভিকর্ষ কেন্দ্রে কাজ করে এবং ঐ বিন্দুতে কিয়াশীল প্রত্যয়নী বল ও ঐ বিন্দুর দূরত্ব ভেক্টরের মধ্যবর্তী কোণ 90o এবং F = -mgsinθ আর ঝুলন বা ঘূর্ণন বিন্দু থেকে দূরত্ব L) এখন, যদি খুব ক্ষুদ্র হয়(4o অপেক্ষা ছোট) তাহলে আমরা বলতে পারি, sinq = q (প্রায়) তাহলে, F = – mg θ এবং
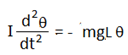
এখানে I হল ঘূর্ণন অক্ষের সাপেক্ষে জড়তার ভ্রামক।
বা,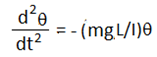
এখন যেহেতু ঘূর্ণন এখানে বৃত্তাকার তাই আমরা বলতে পারি, x ∝ θ
তাহলে, ![]() অর্থাৎ
অর্থাৎ ![]() যেখানে, ω2 = (mgL/I)
যেখানে, ω2 = (mgL/I)
এ ধরণের দোলক দিয়ে সরল দোলকের চেয়ে নিখুঁতভাবে অভিকর্ষজ ত্বরণ g এর মান নির্ণয় করা যায়। এ ধরণের pendulum কে বলে compound pendulum। এর সমতুল্য সরল দোলকের কার্যকর দৈর্ঘ্য , d = I/mL .
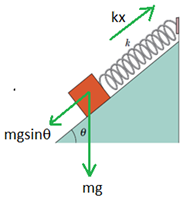
সমস্যা ১৩: আবারও স্প্রিংঃ
(1) স্প্রিং ধ্রুবক k আর বস্তুর ভর m ,গতির সমীকরণটি নির্ণয় করতে হবে।
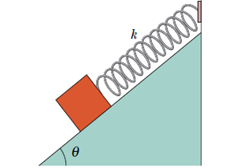
ক্রিয়াশীল মোট প্রত্যয়নী বল, F = mgsinθ – kx
বা, 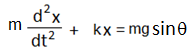
বা,![]() যেখানে, ω2 = k/m এটাই গতির সমীকরণ
যেখানে, ω2 = k/m এটাই গতির সমীকরণ
সমস্যা ১৪: তিনটা স্প্রিং ও দুইটা বস্তুঃ
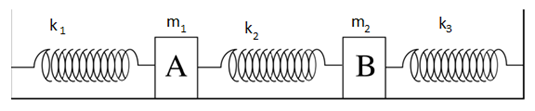
নগণ্য ভরের প্রত্যেক স্প্রিং এর স্প্রিং ধ্রুবক k1 , k2 , k3 আর A এর ভর m1 এবং B এর ভর m2 এর গতির সমীকরণগুলো বের করতে হবে।
সমাধানঃ
প্রথমে নিচের ছবিটি লক্ষ্য করঃ
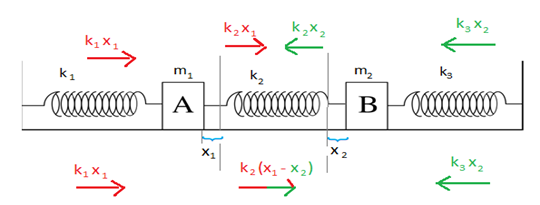
ধরি, m1 ভরের বস্তু a1 ত্বরণে এবং m2 ভরের বস্তু a2 ত্বরণে গতিশীল।
m1 ভরের বস্তুর জন্য, k1x1 + k2(x1 – x2) = m1a1
বা, 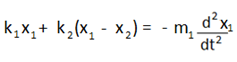 (ঋণাত্মক চিহ্ন কেন এলো ? :O )
(ঋণাত্মক চিহ্ন কেন এলো ? :O )
বা, ![]() এটি ১ম বস্তুর গতির সমীকরণ।
এটি ১ম বস্তুর গতির সমীকরণ।
এবার, m2 ভরের বস্তুর জন্য, – k3x2 + k2(x1 – x2) = m2a2
বা, 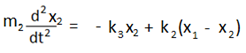 এটি ২য় বস্তুর গতির সমীকরণ।
এটি ২য় বস্তুর গতির সমীকরণ।
সমস্যা ১৫: স্প্রিং ও পুলিঃ
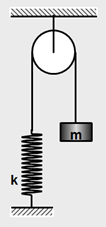
(১) একটি m ভরের বস্তু একটি নগন্য ভরের পুলির মধ্যে দিয়ে একটি নগণ্য ভরের স্প্রিং এর সাথে চিত্রের মত যুক্ত। স্প্রিং ধ্রুবক k । গতির সমীকরণটি নির্ণয় করতে হবে।
সমাধানঃ
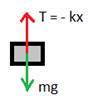
ক্রিয়াশীল মোট প্রত্যয়নী বল, F । এক্ষেত্রে, বস্তুর যতখানি সরণ হবে স্প্রিং এর প্রসারণ ততখানিই হবে।
এখানে, mg – T = F এবং T = – kx
অর্থাৎ F = mg + kx
বা, 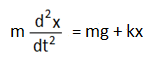 এটিই গতির সমীকরণ।
এটিই গতির সমীকরণ।
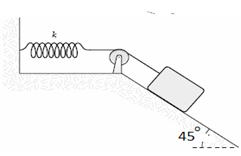
সমস্যা ১৬: পুলি , বস্তু যখন হেলানো তলেঃ
চিত্রের সিস্টেমটির গতির সমীকরণ বের করতে হবে (যেখানে স্প্রিং ও পুলি নগণ্য ভরের)।
সমাধানঃ
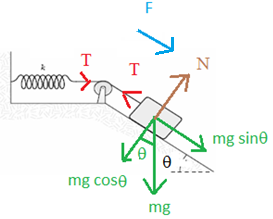
ক্রিয়াশীল মোট প্রত্যয়নী বল, F । এক্ষেত্রে, বস্তুর যতখানি সরণ হবে স্প্রিং এর প্রসারণ ততখানিই হবে।
এখানে, mgsin θ – T = F এবং T = – kx
অর্থাৎ F = mg sin θ + kx
বা,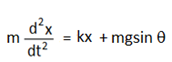 এটিই গতির সমীকরণ।
এটিই গতির সমীকরণ।
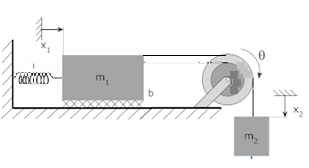
সমস্যা ১৭: পুলি , বস্তু যখন টেবিলের উপরঃ
চিত্রের সিস্টেমটির গতির সমীকরণ বের করতে হবে (যেখানে স্প্রিং ও পুলি নগণ্য ভরের)।
সমাধানঃ
উভয় বস্তুই a ত্বরণে গতিশীল এবং m2 এর x পরিমাণ সরণ হলে m1 এরও x পরিমাণ সরণ হয় এবং স্প্রিং এরও x পরিমাণ প্রসারণ হয়।
m2 বস্তুর জন্য, m2g – T = m2a এবং m1 বস্তুর জন্য, T – kx = m1a
সমীকরণ দুইটিকে যোগ করে আমরা পাই,
m2g – kx = (m1 + m2)a
বা, (m1 + m2)a + kx = m2g
বা, 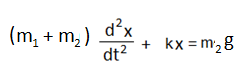
এটিই গতির সমীকরণ যেখানে, ω2 = k / (m1 + m2 )।
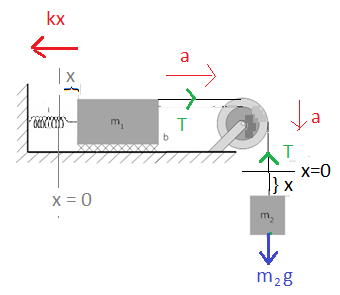
সমস্যা ১৮: স্প্রিং যখন পুলিতে ঝুলানো বস্তুর সাথে আরেক বস্তু যখন টেবিলের উপরঃ
সুষম ত্বরণে চলমান ব্লক দুইটি দ্বারা গঠিত সিস্টেমটির গতির সমীকরণ বের করো (যেখানে স্প্রিং ও পুলি নগণ্য ভরের):
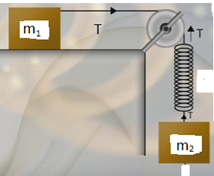
সমাধানঃ
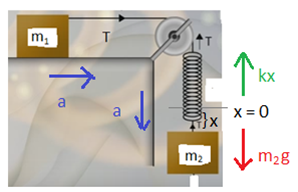
উভয় বস্তুই a ত্বরণে গতিশীল এবং m2 এর x পরিমাণ সরণ হলে স্প্রিং এরও x পরিমাণ প্রসারণ হয়।
m1 বস্তুর জন্য, T = m1a
এখন, সম্পূর্ণ টান, T স্প্রিং এর প্রসারণে প্রত্যয়নী বল হিসেবে কাজ করছে। তাই,
T = kx . অর্থাৎ kx = m1a.
m2 বস্তুর জন্য, m2g – T = m2a
বা, m2g – kx = m2a
বা, m2g – kx – kx = m2a – m1a
বা, m2g – 2kx = (m2 – m1)a
বা, ![]() এটিই গতির সমীকরণ।
এটিই গতির সমীকরণ।
(বি.দ্র. সমস্যা ১৫ এবং ১৬ সাধারণ oscillation, এগুলো SHM নয়।)
শেষের আগে একটু কথাঃ
আমরা আমাদের যাবতীয় হিসেব নিকেশ শক্তির নিত্যতা সূত্র ব্যাবহার করে আরও সহজভাবে করতে পারতাম।
কারণ আমরা জানি, মোট যান্ত্রিক শক্তি = বিভব শক্তি + গতি শক্তি।
কোন স্থিতিস্থাপক বস্তু তার সাম্যাবস্থা থেকে অবস্থানের পরিবর্তন এর জন্য স্থিতিস্থাপক বিভব শক্তি অর্জন করতে পারে।
অর্থাৎ, শক্তির নিত্যতা সূত্র অনুসারে,
kx2/2 + mv2/2 = E
বা, 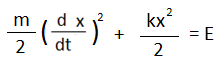 এই সমীকরণটি নতুন কিছুই নয়, আমাদের SHM এর differential equation,
এই সমীকরণটি নতুন কিছুই নয়, আমাদের SHM এর differential equation, ![]() কে x এর সাপেক্ষে integrate করলেই আগের সমীকরণটি পাওয়া যায় কারণ আমরা জানি বল (F) কে সরণের (x) সাপেক্ষে integrate করলে কৃতকাজ পাওয়া যায় আর কৃতকাজ মানেই তো শক্তি (E)। তাই মোট শক্তি হিসেব করে তোমরা পূর্বের সমস্যাগুলো সমাধান করে ফেলতে পারো। আমি আর তা করে দিলাম না, তোমরা নিজেরা চেষ্টা করো। 🙂
কে x এর সাপেক্ষে integrate করলেই আগের সমীকরণটি পাওয়া যায় কারণ আমরা জানি বল (F) কে সরণের (x) সাপেক্ষে integrate করলে কৃতকাজ পাওয়া যায় আর কৃতকাজ মানেই তো শক্তি (E)। তাই মোট শক্তি হিসেব করে তোমরা পূর্বের সমস্যাগুলো সমাধান করে ফেলতে পারো। আমি আর তা করে দিলাম না, তোমরা নিজেরা চেষ্টা করো। 🙂
আমি এখানে কেবল সমীকরণগুলো বের করে দিয়েছি আশা করি তোমরা কৌণিক কম্পাংক, কম্পাংক, পর্যায়কাল, বিস্তার, বেগ, ত্বরণ এগুলো বের করতে পারবে।
আজ তাহলে এ পর্যন্তই। সরল ছন্দিত স্পন্দন (SHM) নিয়ে আরও অনেক জটিল সমস্যা বানানো যায়। আশা করি, সেগুলো এখন তোমরা নিজেরাই সমাধান করতে পারবে। 🙂


অনেক খাটছিস দোস্ত 😀 সিম্পলি ওয়াও 😀
ধন্যবাদ। 😀
awesome =D
Great
really awesome….বাট আলসেমির জন্য যদিও সব পড়ি নাই