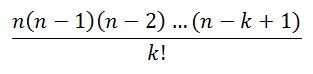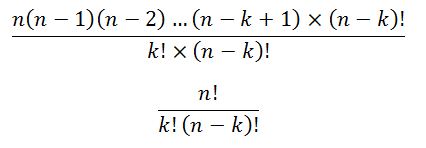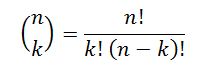হাবিজাবির আগের পর্বগুলোতে আমরা permutation বা বিন্যাস শিখেছি। এবারে আমরা combination বা সমাবেশ শিখব। প্রথমে combination এর সংজ্ঞা দিয়ে নেই, তারপর উদাহরণে যাব।
Combination:: কতকগুলো নির্দিষ্ট উপাদানের সমষ্টিকে Combination বলা হবে যদি সেখানে উপাদানগুলো কিভাবে সজ্জিত আছে তা অবিবেচ্য হয়।
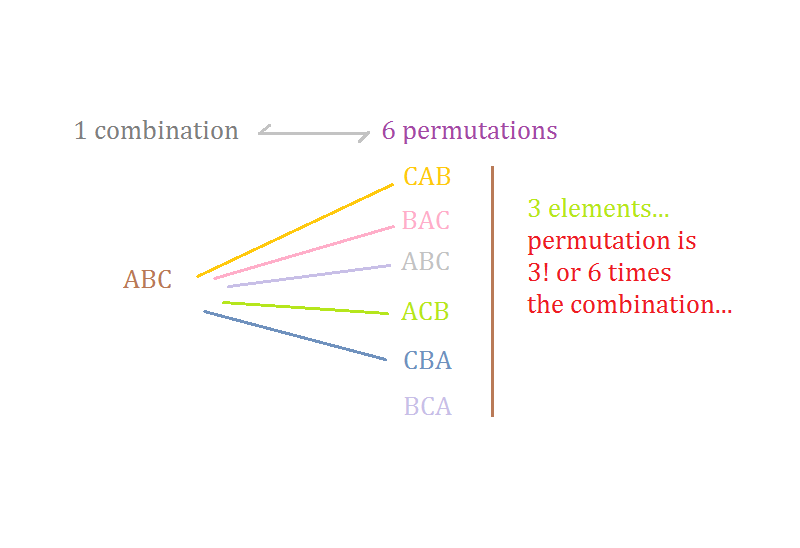
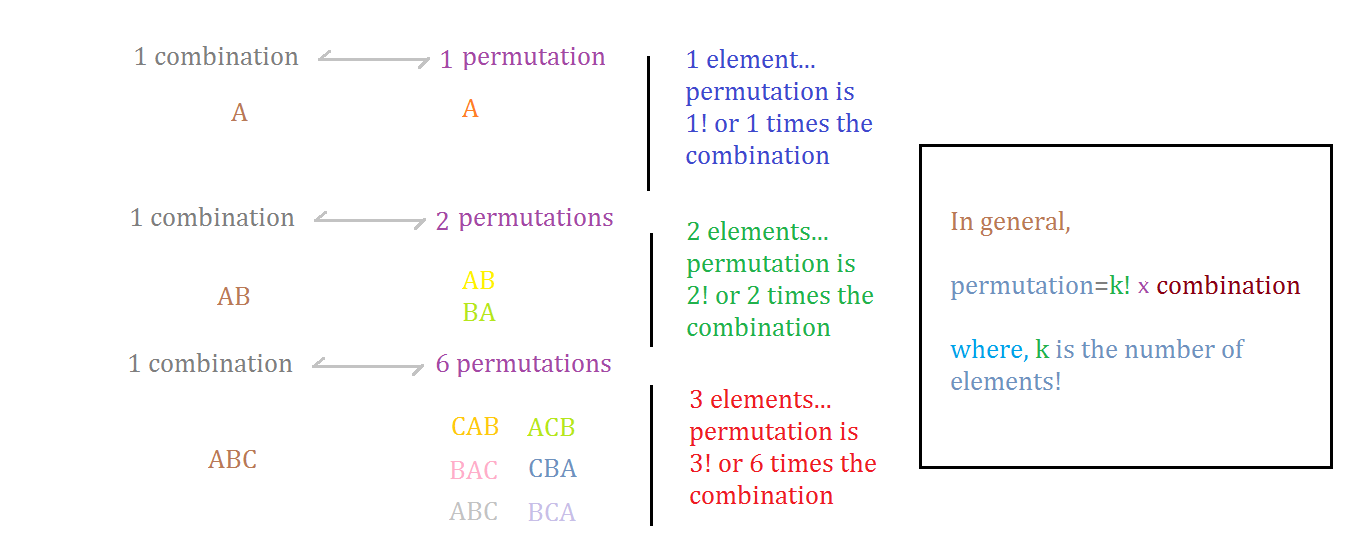
মনে করি, চারটি উপাদানের সেট {A, B, C, D} থেকে তিনটি উপাদান বেছে নিয়ে আমরা combination বানাব। এরকম combination হতে পারে চারটি- ABC, ACD, BCD, ABD । অর্থাৎ, আমরা তিনটে উপাদানের কতগুলো সমষ্টি থাকতে পারে তা খুঁজে বের করেছি। যদি আমাদের permutation বের করতে বলত? তবে আমরা দেখতাম যে, 4×3×2=24 টি permutation আছে। Combination 4 টি আর permutation 24 টি কেন? Permutation এ উপাদানগুলো কিভাবে সজ্জিত আছে তাও বিবেচনার বিষয়! একটা combination ABC নিই। ABC কে আমরা 3! বা 6 উপায়ে লিখতে পারি। এই 6 টি উপায় হচ্ছে ABC, BCA, CBA, ACB, BAC, CAB । এদের প্রত্যেকটিই একেকটি permutation। কারণ, প্রত্যেকটিতে A, B ও C এর অবস্থান বা ক্রম অন্যগুলোর থেকে আলাদা। কিন্তু, combination যখন বের করতে হয় তখন আমরা শুধু কি কি উপাদান উপস্থিত আছে তা বিবেচনায় রাখি। উপরে ABC এর 6 টি permutation এর প্রত্যেকটিতেই তিনটে নির্দিষ্ট উপাদান উপস্থিত (A, B, C)। তাই এই 6 টি permutation কেবলমাত্র একটি combination কে নির্দেশ করে।
Combination এ কোনো একটি উপাদান একবারের বেশি ব্যবহৃত হতে পারে। যেমন, AABC আর ACAB একই combination।
এবারে কিছু সমস্যার সমাধান করে হাত গরম করা যাক!
- {A, B, C, D, E} সেট থেকে 2 টি করে উপাদান বেছে নিয়ে কতগুলো combination পাওয়া যায় তার হিসাব করতে হবে যখন,
- দুটো উপাদানই আলাদা হতে পারে;
- দুটো উপাদান একও হতে পারে।
- {A, B, C, D, E} সেট থেকে 3 টি করে উপাদান বেছে নিয়ে কতগুলো combination পাওয়া যায় তার হিসাব করতে হবে এবার যদি,
- উপাদান তিনটি আলাদা হয়;
- বেছে নেয়া উপাদান একবারের বেশি ব্যবহার করা যায়।
[উপরের সমস্যাগুলোর সমাধান করার চেষ্টা করতে থাকো। না পারলে শেষ পর্যন্ত পড়ে যাও।]
এবারে আমরা কাঠখোট্টা নিয়ম প্রতিষ্ঠা করার চেষ্টা করব। আমাদের সাধারণ সমস্যাটি হচ্ছে,
“k সংখ্যক উপাদান দ্বারা তৈরি combination সংখ্যা খুঁজে বের করা যেখানে উপাদানগুলো n সংখ্যক উপাদানের সেট থেকে বেছে নেয়া।”
এই সমস্যার সমাধানের জন্য আমরা প্রথমে k সংখ্যক উপাদানে তৈরি permutation সংখ্যা বের করব। আগের পর্বগুলোতে এরকম গণনা আমরা করতে শিখেছিলাম।
n সংখ্যক উপাদান থেকে k টি উপাদান নির্দিষ্ট ক্রমে বাছার উপায়,
আমরা যেটা পেলাম তাতে ক্রম বিবেচনা করা হয়েছে। কিন্তু, combination এর জন্য ক্রম অপ্রয়োজনীয়। আর তাই, আমাদের ক্রম নিরপেক্ষ হতে হবে।
ধরা যাক, k টি উপাদানের combination আছে আমাদের কাছে। একে permutation বানাতে হলে কি করতে হবে? k সংখ্যক distinct উপাদান নিজেদের মধ্যে কত উপায়ে বিন্যস্ত হতে পারে তা নির্ণয় করতে হবে। আর k টি উপাদানের নিজেদের মধ্যে বিন্যস্ত হওয়ার উপায় হল k! । অর্থাৎ, combination সংখ্যার সাথে k! গুণ করে দিলেই permutation পাওয়া যায়। উল্টোভাবে, permutation কে k! দ্বারা ভাগ করলে combination পাওয়া যায়।
উপরের টেকনিক ব্যবহার করলে আমরা সাধারণ সমস্যাটির উত্তর পেয়ে যাচ্ছি,
এটাকে আমরা সাজিয়ে লিখব,
এটিকে সাধারণত C(n, k) বা বা nCk দ্বারা প্রকাশ করা হয়। মানে,
উপরের ফর্মুলা দিয়ে আমরা সহজেই combination সংখ্যা হিসাব করে ফেলতে পারি।
কয়েকটি সহজ সমস্যার সমাধান করে ফেল তবে,
- 75 টি উপাদানের একটি সেট থেকে 15 টি উপাদান দ্বারা গঠিত combination এর সংখ্যা কত? (যদি কোনো উপাদান রিপিট না করা যায়)
- 75 টি উপাদানের একটি সেট থেকে 50 টি উপাদান দ্বারা গঠিত combination এর সংখ্যা কত? (যদি কোনো উপাদান রিপিট না করা যায়)
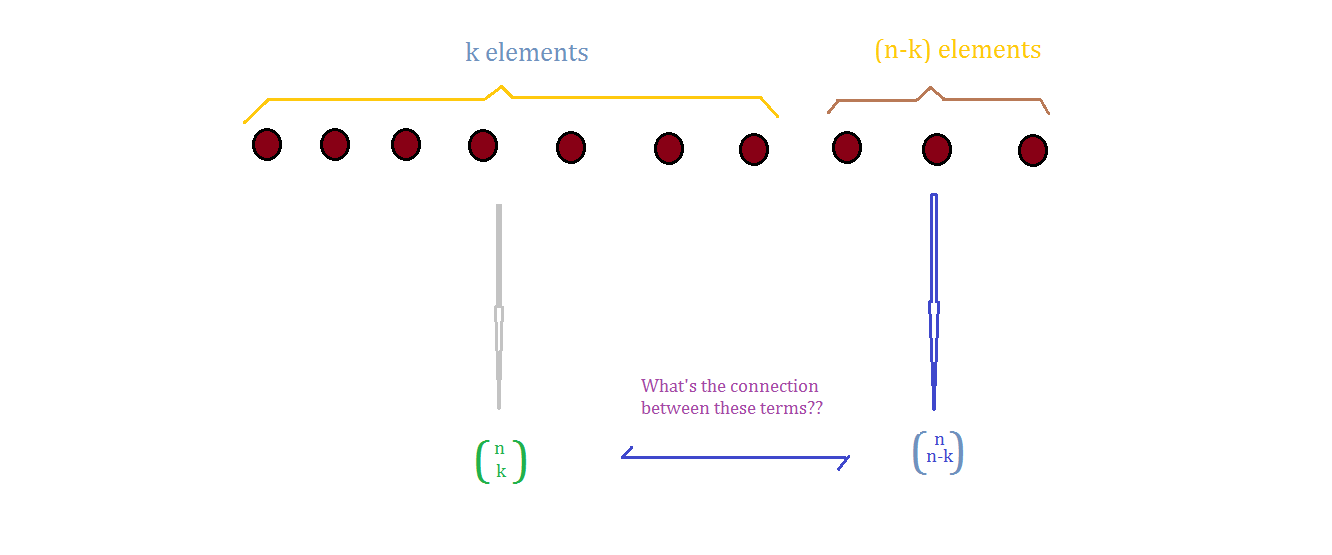
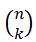আর 
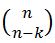এর সম্পর্ক কি?
এবারে শুরুতে দেয়া কিছু সমস্যার সমাধানের জন্য কিছু Hint দেই।
{A, B, C, D, E} থেকে 2 টি উপাদান বাছার জন্য প্রথমে একটা উপাদান ফিক্সড করে নাও। যেমন, ধরে নিলাম A আছে। এবারে চারটা উপাদান বাকি থাকায় দ্বিতীয় উপাদান বাছার জন্য অপশন পাব 4 টি। এরপরে B কে ফিক্সড ধরে নিলে দ্বিতীয় উপাদানের জন্য অপশন থাকবে 3 টি (4 টি নয় কারণ AB আমরা আগেই হিসাব করে ফেলেছি যখন A কে ফিক্সড ধরে নিয়েছিলাম)। এভাবে আগালে সহজেই সমাবেশ সংখ্যা বের করে ফেলতে পারবে।
আরেকটা Hint দিতে হয়। ‘5 টি উপাদান থেকে 2 টি উপাদান বাছা’ আর ‘5 টি উপাদান থেকে 3 টি উপাদান বাছা’ কিন্তু একই কথা! এটা আর ব্যাখ্যা করলাম না। এতক্ষণ ধরে মনোযোগ দিয়ে পড়ে আসলে একটু চেষ্টা করলেই ব্যাপারটা বুঝে যাবে।
ATM Jahid Hasan
Latest posts by ATM Jahid Hasan (see all)
- আজ আমি বৃষ্টি দেখেছি! - February 2, 2016
- কুইজ :: Nov 2015; Week 2 - November 29, 2015
- কুইজ :: Nov 2015; Week 1 - November 12, 2015