আজ আমরা যা শিখবো, তা আমরা ছোটবেলাতেই শিখে এসেছি। অনেকে হয়তো নামটা শুধু জানতাম না!
N(AUB) = N(A) + N(B) – N(A∩B)
এটা দেখে পরিচিত মনে হচ্ছে না? হ্যা এটাই! 😀 ধর তোমাকে বলা হল, ১ থেকে ৩০-র মধ্যে এমন কয়টি সংখ্যা আছে, যা ৩ অথবা ৫ দিয়ে বিভাজ্য।
আমরা ৩ দিয়ে বিভাজ্য সংখ্যাগুলো বের করতে পারি এভাবেঃ N(A) = 30/3 = 10
এই সংখ্যাগুলো হলঃ 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
একই ভাবে ৫ দ্বারা বিভাজ্য সংখ্যাঃ N(B) = 30/5 = 6
এই সংখ্যাগুলো হলঃ 5, 10, 15, 20, 25, 30
এখন খেয়াল কর, 15, 30 এই সংখ্যা দু’টি আমরা দুই বার হিসেব করেছি। তাহলে আমাদেরকে একবার করে এটা বাদ দিতে হবে। এরা হল ১৫-এর গুণিতক। ১৫ হল ৩ এবং ৫-এর লসাগু(LCM)। এখনঃ N(A∩B) = 30/15 = 2!
তাহলে আমরা আমাদের উত্তর পাচ্ছিঃ N(AUB) = N(A) + N(B) – N(A∩B)
একইভাবে তিনটি সংখ্যার জন্য এটি বের করতে চাইলে আমরা করতামঃ
N(AUBUC) = N(A) + N(B) + N(C) – N(A∩B) – N(B∩C) – N(A∩C) + N(A∩B∩C)
চিহ্নগুলো খেয়াল কর। বিজোড় সংখ্যক উপাদানের ইন্টারসেকশন হলে সেটা যোগ করতিছি, আর জোড় সংখ্যক হলে বিয়োগ করতেছি। তাহলে N(AUBUCUD)-এর মান কত হবে বল তো?
আশা করি পেরেছ সবাই।
N(AUBUCUD) = N(A)+N(B)+N(C)+N(D) – N(A∩B) – N(B∩C) – N(C∩D)-N(A∩D)+N(A∩B∩C)+N(B∩C∩D)+N(A∩C∩D)+N(A∩B∩D)-N(A∩B∩C∩D)
খুবই সোজা। কিন্তু সমস্যা হল, আমাদেরকে এটা কোডে ইমপ্লিমেন্ট করতে হবে। আর দুই, তিন বা চার উপাদানের জন্য কাজটা মোটামুটি সহজ হলেও যখন উপাদান সংখ্যা ১৫ দিবে, তখন কীভাবে করবো? তখন কী করা যাবে সেটা নিয়েই আজকের এই লেখাটি!
এজন্য আমরা প্রথমেই সমস্যাটাকে একটু ভিন্ন দৃষ্টি থেকে দেখার চেষ্টা করবো। ধরা যাক, আমার কাছে চারটা উপাদান আছে।
এখন চারটি উপাদানের ক্ষেত্রেই আমাদের কাছে দুইটি অপশন আছে। আমরা হয় সেই উপাদানটি গ্রহণ করবো, না হয় করবো না। গ্রহণ করলে আমরা সেটা 1 দ্বারা রিপ্রেজেন্ট করবো, আর না করলে 0। প্রাথমিকভাবে কোনো উপাদানই গ্রহণ করা হয়নি।
এখন আমরা এখান থেকে যেকোনো একটি উপাদান গ্রহণ করবো। কতভাবে করতে পারি? চারভাবে।
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
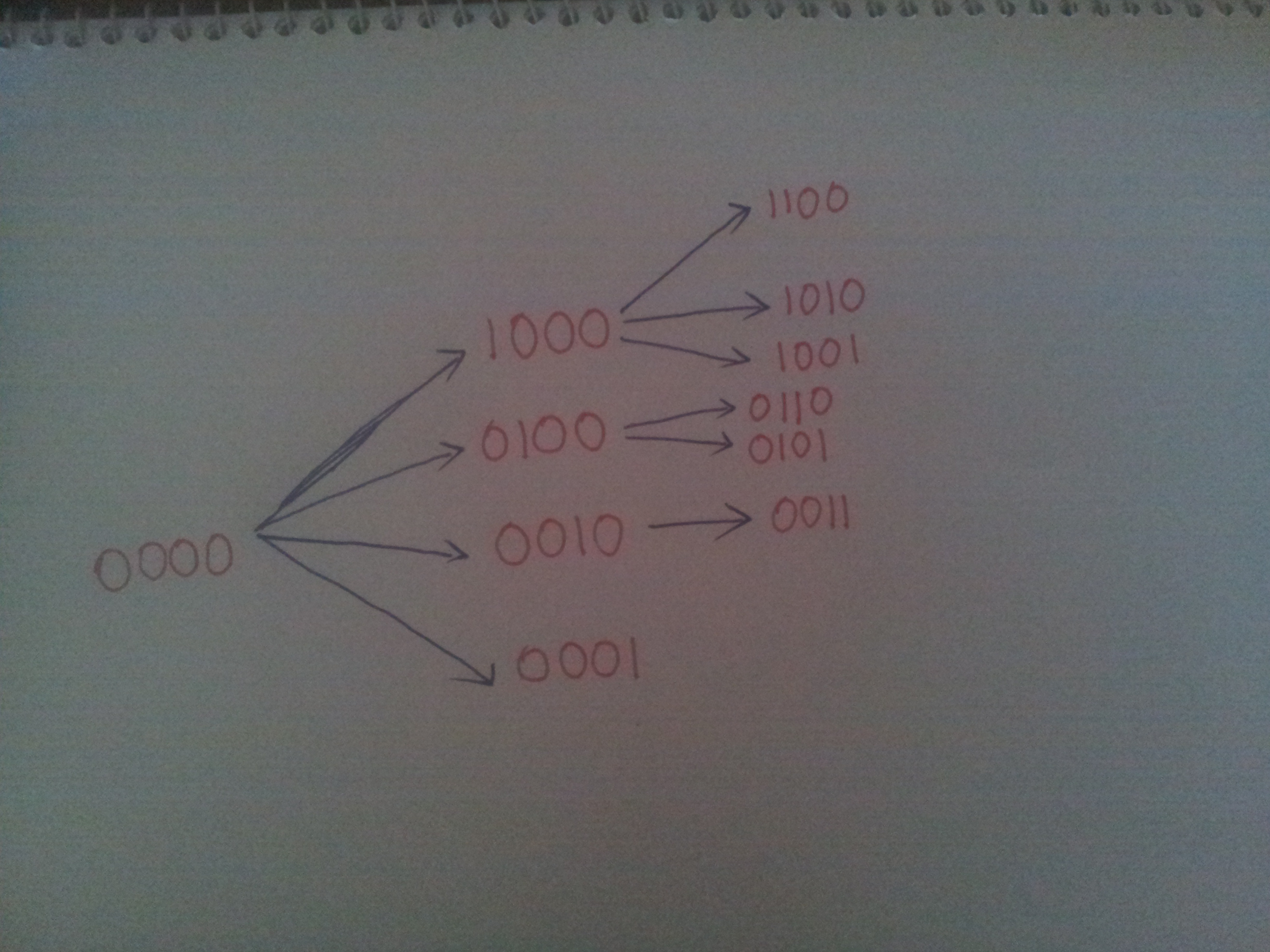
এবার আমরা একটি উপাদান নেওয়া হয়েছে এই সাপেক্ষে আরেকটি উপাদান (যার ইনডেক্স অবশ্যই ইতোমধ্যে নেওয়া উপাদানটির চেয়ে বড়) কতভাবে নিতে পারি? এটা নির্ভর করবে, আমরা ইতোমধ্যে যে উপাদানটি নিয়েছি, তার ইনডেক্স কত তার উপর।
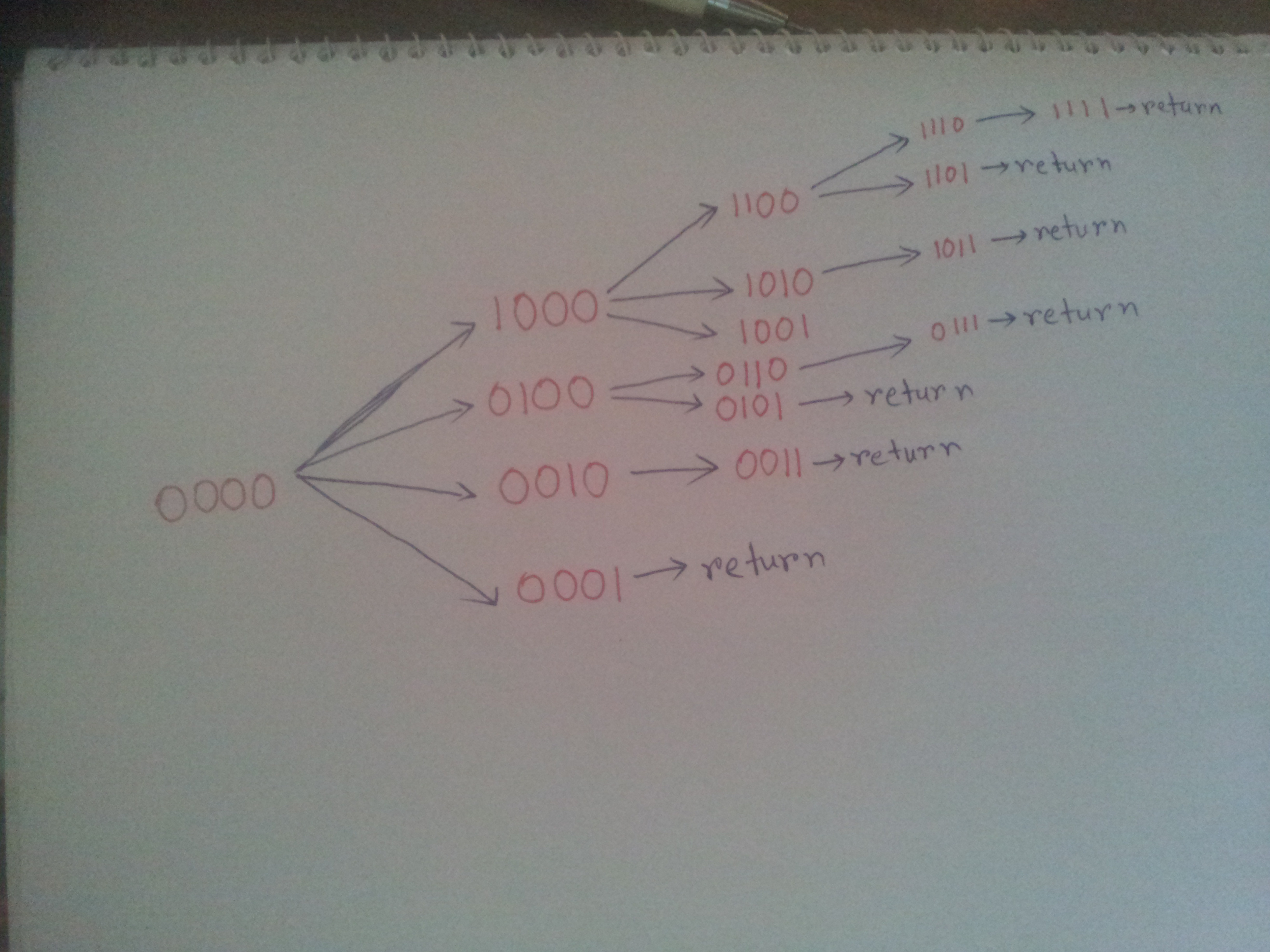
খেয়াল কর শেষটি থেকে আমরা দ্বিতীয় আর কোনো ইলিমেন্ট নিতে পারিনি। বল তো কেন? কারণ ইতোমধ্যে সিলেক্ট করা উপাদানটি অ্যারের শেষ উপাদান ছিল! /* Spoiler Alert! 😛 আমাদের রিকার্শনের Base Case কী? */
বাকি কাজটা সোজা। এবার দুইটা সিলেক্ট হয়ে গেছে, এই অবস্থা থেকে তিনটা সিলেক্ট করতে হবে। তারপর তিনটা সিলেক্ট হয়ে গেছে এই অবস্থা থেকে চারটা সিলেক্ট করতে হবে!
আর আমরা যখনই এরকম শাখা প্রশাখা বিস্তার করতে দেখবো, তখনই আশ্রয় নিতে পারি রিকার্শনের!
এজন্য আমাদের একটা ফাংশন লিখতে হবে, যার প্যারামিটার হিসেবে দিতে হবেঃ
(১) ইতোমধ্যে যে সব উপাদান নেওয়া হয়েছে, তাদের “Intersection”-এর মান। উপাদান সংখ্যা একটি হলে শুধু সেটির মান দিলেই হবে। LCM বের করার ক্ষেত্রে আমরা 1-এর সাথে সে সংখ্যার LCM বের করলেই হবে!
(২) ইতোমধ্যে যে সব উপাদান সিলেক্ট করা হয়েছে, তাদের মধ্যে সর্বশেষটির ইনডেক্স।
(৩) ইতোমধ্যে যতটি সংখ্যা নেওয়া হয়েছে, তার সংখ্যা। ধরা যাক, এটা n। এরপর আমরা আরেকটি উপাদান নিলে হবে n+1। এটা প্যারামিটার হিসেবে নিতে হচ্ছে, কারণ n+1 জোড় হলে আমরা ইউনিয়নের মান বিয়োগ করবো, আর বিজোড় হলে করবো যোগ।
(৪) অ্যারেটা তো পাঠাতেই হবে, নাহলে কাজ করবো কী দিয়ে? 😛
আরও কিছু পাঠাতে হতে পারে, পরিস্থিতি সাপেক্ষে!
এখন প্রশ্ন হল, Base Case কী হবে?
খেয়াল কর, আমরা যখন দেখেছি সর্বশেষ সিলেক্ট করা ইলিমেন্টটি অ্যারের শেষ উপাদান তখন রিটার্ন করেছি। তার মানে এটাই Base Case। এজন্য আমাদের প্যারামিটার হিসেবে মোট উপাদান সংখ্যাও পাঠাতে হবে!
আর ফাংশনের ভেতরে কী করবো?
বেশি কিছু না। 😛
- ইন্টারসেকশন বের করবো
- যোগ কিংবা বিয়োগ করবো
- ফাংশন রিকল করবো
এবার কোডটা নিজে লেখার চেষ্টা কর। আমাদের সমস্যাটা হল এরকম, ১ থেকে ১০০০ পর্যন্ত কতগুলা সংখ্যা ২, ৩, ৫, ৬, ৭, ১১, ১৩, ১৫, ১৭-এদের যে কোনো এক বা একাধিক সংখ্যা দ্বারা বিভাজ্য, তা বের করতে হবে। এখানে ৯ টি সংখ্যার মধ্যে ইনক্লুশন এক্সক্লুশন করতে হবে।
এটা সমাধান করার জন্য তোমার lcm বের করার ফাংশন লাগবে। এটা সহ প্রাথমিক কাজগুলো আমি করে দিচ্ছি।
#include <stdio.h>
int ans;
int gcd(int a, int b) {
while(b)
b ^= a ^= b ^= a %= b;
return a;
}
int lcm( int a, int b) {
return a*b/gcd(a,b);
}
int recurs(int ara[], int i, int j, int num, int numofele, int n) {
// i = shorboshes selected element er index
// j = ekhon porjonto ja newa hoiche, tader lcm
// num == ekhon porjonto joto gula selected hoiche
// numofele = total element shonkha
// n = 1000, amra 1 theke 1000 porjonto ber kortichi
}
int main() {
int n, m, i;
int ara[] = {2, 3, 5, 6, 7, 11, 13, 15, 17};
n = 1000;
ans = 0;
m = 9;
recurs(ara, 0, 1, 0, m, n);
/* ei call ta te kon value koto hishebe pathacchi sheta
valo moto bujhe er por code lekha shuru korio */
printf("Answer = %d\n", ans);
return 0;
}
তোমার কাজ হবে recurs নামের ফাংশনটা কমপ্লিট করা। অন্তত এক ঘন্টা চেষ্টা করেও যদি না পার, তাহলে নিচে আমার কোড দেখে বোঝার চেষ্টা কর। এরপরও সমস্যা থাকলে কমেন্টে জানাও। 🙂
int recurs(int ara[], int i, int j, int num, int numofele, int n) {
// i = shorboshes selected element er index
// j = ekhon porjonto ja newa hoiche, tader lcm
// num == ekhon porjonto joto gula selected hoiche
// numofele = total element shonkha
// n = 1000, amra 1 theke 1000 porjonto ber kortichi
if (i+1 == numofele) return 0;
int x, y;
for (x = i; x <numofele; x++) {
y = lcm(ara[x], j);
if ((num+1)%2==1) ans+=(n/y);
else ans-=(n/y);
recurs(ara, x+1, y, num+1, numofele, n);
}
}
ইনক্লুশন এক্সক্লুশন কীভাবে করে দেখা হল। এবার এভাবে কিছু প্রবলেম সলভ করা যাক!
হ্যাপি কোডিং! 🙂

nice post… exclusive or ( ^ ) use kore ki vabe GCD ber korlen aita niye akta post korle ektu valo hoto 😀
আসলে আমরা ইউক্লিডের পদ্ধতিতে যে জিসিডি বের করি, সেখানে ২ টা নাম্বার swap করতে হয়। সে swapping-এর কাজটা বিটওয়াইজ অপারেটর দিয়ে কীভাবে করতে হয়, সেটা কিন্তু এখানে দেখানো হয়েছে! 🙂
hmm vaiya exclusive or use kore GCD ber korar way ta bujte parlam… 🙂 first a na buje comment korar jonno sorry :p r apnar proti ta post e amar onek valo lage…. asha kori samne aro onek valo kono topics niye discuss korben sei ashay roylam 🙂
ekhane je code ta kora ache er output ki asbe??ami ektu confused ekta output niye..tai.. :/
asole ekhane jodi amra 1 theke 100 er moddhe kotogulo sonkha 2,3 dara bivajjo eta ber korte caile output ki 67 hobe naki 83 hobe??
২ আর ৩ উভয়ের দ্বারা, নাকি ২ কিংবা ৩ যেকোনোটি দ্বারা? নাকি কেবল (হয় ২ অথবা কেবল ৩) দ্বারা? এই কীওয়ার্ডগুলো বুঝতে পারলে আউটপূটটাও বুঝবেন আশা করি। 🙂
if (i+1 == numofele) return 0;
এখানে শুধু i হবে। i+1 দিলে আউটপুট ভুল আসে।