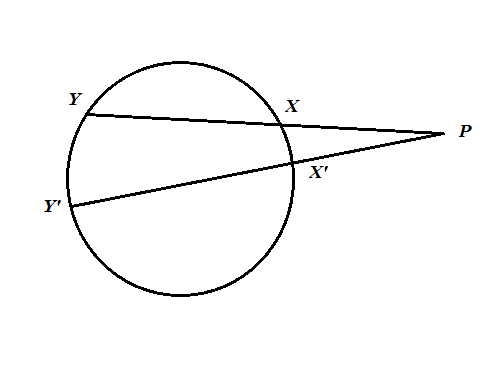
সমস্যা-১: একটি বিন্দু P থেকে অংকিত দুটি রেখা একটি বৃত্তকে X, Y ও X’, Y’ বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, PX.PY=PX’.PY’
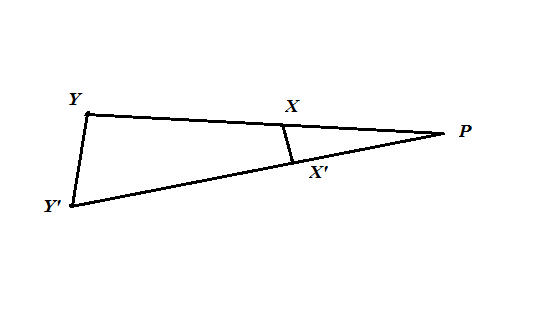
সমাধান: প্রথমে X, X’ ও Y, Y’ যোগ করি।
এখানে XX’Y’Y একটি বৃত্তস্থ চতুর্ভুজ। ফলে, কোণ X’Y’Y + কোণ X’XY = 180 ডিগ্রি । আবার, কোণ X’XY + কোণ PXX’ = 180 ডিগ্রি। ফলে, কোণ PXX’ = কোণ X’Y’Y । একইভাবে, কোণ PX’X = কোণ XYY’ । এখন ত্রিভুজ PXX’ ও ত্রিভুজ PYY’ এ কোণ PXX’ = কোণ X’Y’Y ; কোণ PX’X = কোণ XYY’ এবং XPP’ সাধারণ কোণ। ফলে, ত্রিভুজ দুটি সদৃশ।
এ ব্যাপারে আরো বিস্তারিত জানার জন্য Power of a point আর্টিকেলটি পড়তে পার।
সমস্যা-২: x0+x1+x2+…+xn=1 এবং n জোড় সংখ্যা হলে x এর মান কত?
সমাধান: x এর ঘাত যদি জোড় হয় তাহলে আমরা সবসময়ই ধনাত্মক সংখ্যা পাব। কিন্তু ঘাত যদি বিজোড় হয় তাহলে ঋণাত্মক সংখ্যার জন্য ঋণাত্মক সংখ্যা পাওয়া যায়। সমীকরণের ডানপাশে 1 আছে। যেহেতু যোগফল মাত্র 1 তাই আমাদের একটা alternating sequence এর কথা চিন্তা করতে হবে। যেমন, 1−1+1−1+1=1 । আমরা যদি x এর মান −1 বসাই তাহলেই কিন্তু সমীকরণটি মিলে যায়।
অনেকেই হয়তো অনেক ভেবে চিন্তে x এর মান 0 বের করেছ। কিন্তু, এটি কোনো সমাধান হতে পারে না। কারণ, 00 হচ্ছে undefined বা অসংজ্ঞায়িত। তাই, উত্তর হবে x=−1 ।
সমস্যা-৩: একটা ছোট ছেলের কাছে 48 টা ভিন্ন ধরণের (distinct) বস্তু আছে। প্রতিটা বস্তু 2 টা উপাদানের (কাঁচ বা কাঠ) যেকোনো একটা দিয়ে তৈরি। এদের রঙ 4 ধরণের (লাল, নীল, সবুজ বা হলুদ)। এরা 2 আকারের (ছোট অথবা বড়) এবং 3 আকৃতির (বৃত্তাকার, ত্রিভুজাকার বা বর্গাকার)। ফলে যেকোনো একটা বস্তুকে চারটা শব্দ দিয়ে প্রকাশ করা যায়। যেমন, ‘ছোট নীল বৃত্তাকার কাঁচ’। প্রশ্ন হল, এমন কতগুলো বস্তু আছে যাদের বর্ণনা লিখতে ‘ছোট নীল বৃত্তাকার কাঁচ’- শব্দ 4 টার যেকোনো 2 টা ব্যবহার করতে হয়? (যেমন, ‘বড় নীল বৃত্তাকার কাঠ’)
সমাধান: ‘ছোট নীল বৃত্তাকার কাঁচ’- শব্দ চারটি থেকে যেকোনো দুটি আমাদের বেছে নিতে হবে। এ কাজটি করা যায় 4C2 বা 6 উপায়ে। তাহলে, এ 6 টি উপায়ের সব কাঙ্ক্ষিত বর্ণনা বের করে ফেলা যাক,
- আকার ও রঙের পরিবর্তন: 1×3=3 টি ভিন্ন বস্তু
-
আকার ও আকৃতির পরিবর্তন: 1×2=2 টি ভিন্ন বস্তু
-
আকার ও উপাদানের পরিবর্তন: 1×1=1 টি ভিন্ন বস্তু
-
রঙ ও আকৃতির পরিবর্তন: 3×2=6 টি ভিন্ন বস্তু
-
রঙ ও উপাদানের পরিবর্তন: 3×1=3 টি ভিন্ন বস্তু
-
আকৃতি ও উপাদানের পরিবর্তন : 2×1=1 টি ভিন্ন বস্তু
ফলে, দুই দিক দিয়ে ভিন্ন এমন টাইপের বস্তুর মোট সংখ্যা দাঁড়াবে, 3+2+1+6+3+1=16 টি।
সমস্যা-৪: যেকোনো একটি ত্রিভুজ ABC তে D, E ও F যথাক্রমে BC, AC ও AB এর মধ্যবিন্দু। প্রমাণ করতে হবে যে, DE, EF ও FD মূল ত্রিভুজটিকে চারটি সর্বসম ত্রিভুজে ভাগ করে।
সমাধান:
আমাদেরকে প্রথমে একটি অনুসিদ্ধান্ত মনে করতে হবে।
“একটি ত্রিভুজের যেকোনো দুই বাহুর মধ্যবিন্দুর সংযোগকৃত সরলরেখা ত্রিভুজের তৃতীয় বাহুর অর্ধেক ও সমান্তরাল।”
এই কারণে CEFD একটি সামান্তরিক। এখন আরেকটি কথা মনে করতে হবে। ‘একটি সামান্তরিকের কর্ণ একে দুটি সর্বসম ত্রিভুজে ভাগ করে।’ তাহলে, ত্রিভুজ DEF ≅ ত্রিভুজ CDE । একইভাবে, ত্রিভুজ DEF ≅ ত্রিভুজ AEF; ত্রিভুজ DEF ≅ ত্রিভুজ BDF ।
সুতরাং, ত্রিভুজ DEF ≅ ত্রিভুজ CDE ≅ ত্রিভুজ AEF ≅ ত্রিভুজ BDF ।

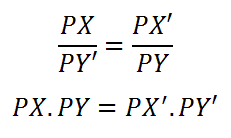
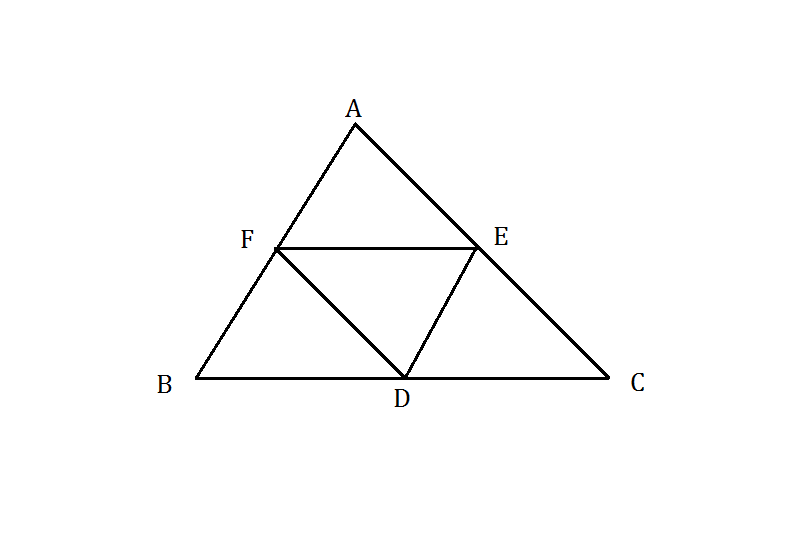

bhaiya…….aro sohoj sohoj problem diyen……kichui pari na