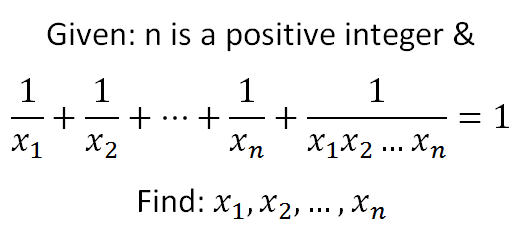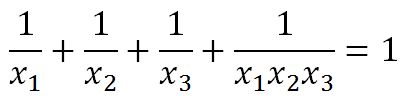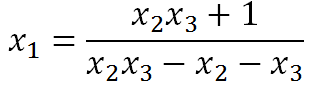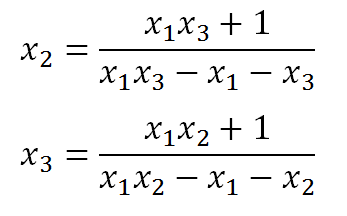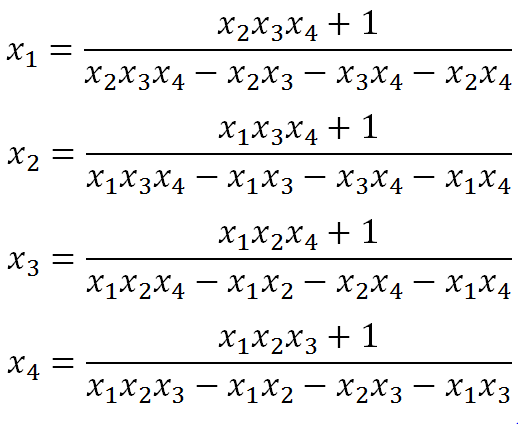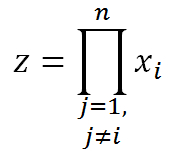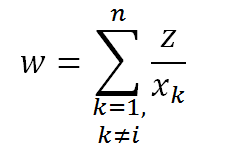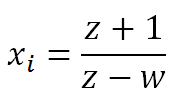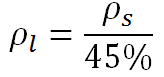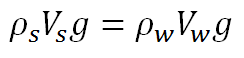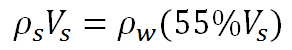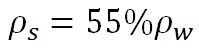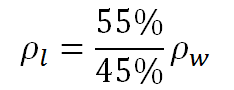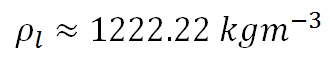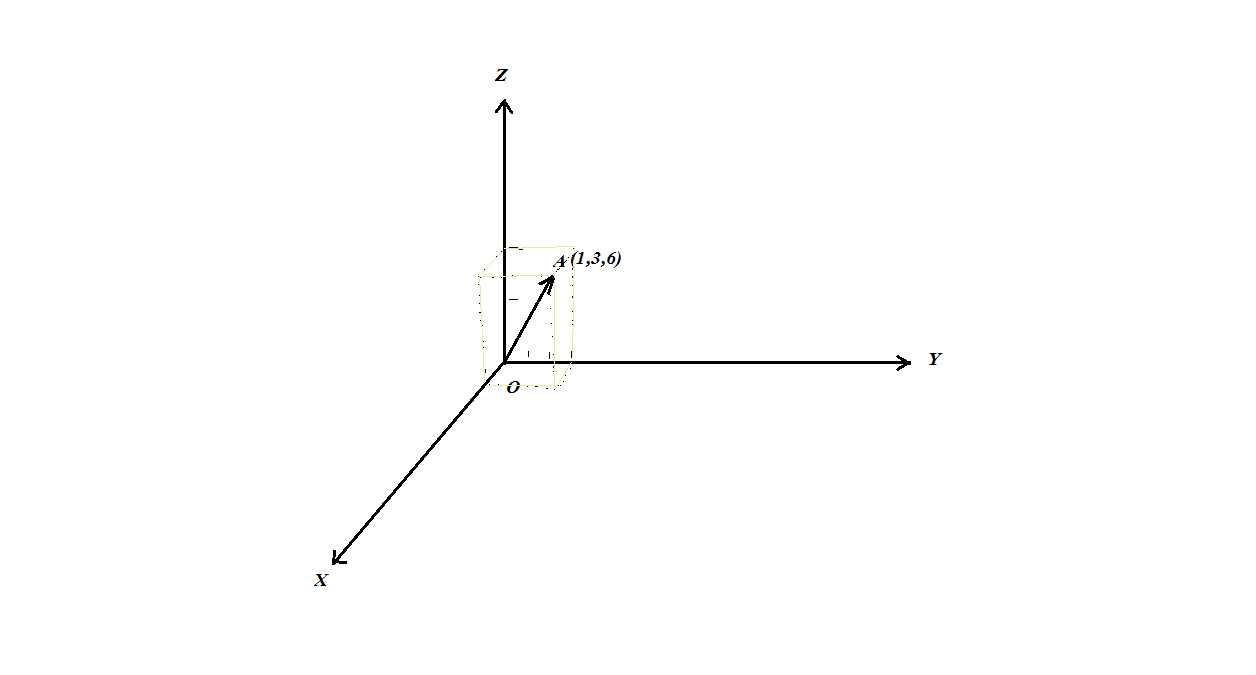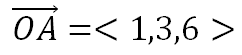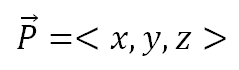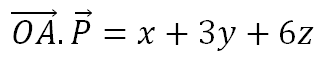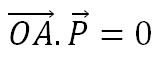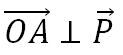সেপ্টেম্বর প্রথম সপ্তাহের কুইজের সমাধান

সমস্যা-১: যদি n যেকোনো ধনাত্মক পূর্ণ সংখ্যা হয় এবং, 1/(x₁)+1/(x₂)+…+1/(x_n)+1/(x₁x₂…x_n)=1 হয়, তাহলে x₁, x₂,…ও x_n এর মান কত?

সমাধান: প্রথমে আমরা সহজ একটা যোগফলের কথা চিন্তা করি। ধরি, n=3, তাহলে,

এই সমীকরনটিকে x₁x₂x₃ দ্বারা গুণ করে পাব,

ধরা যাক, আমরা x₁ এর মান বের করতে চাই। এ কারণে আমাদেরকে সমীকরণটাকে একটু সাজিয়ে লিখতে হবে।

একইভাবে আমরা x₂ ও x₃ এর মানও বের করে ফেলতে পারব।

এভাবে আমরা n এর অন্যান্য মানের জন্যও মান বের করার চেষ্টা করতে আরি। আচ্ছা, যদি n=4 হত তাহলে সমাধানগুলো কেমন হত? নিচের সমীকরনগুলো দেখলেই বুঝা যাবে!

কোনো প্যাটার্ন চোখে পড়ছে? ভালোমত লক্ষ্য করে থাকলে পড়ার কথা। যেই x এর সমাধান বের করতে হবে সেটা বাদে অন্য সব x এর গুণফল উপরে লেখা হয়েছে। সাথে আছে একটা 1 । আর ভগ্নাংশের নিচে আবার সেই গুণফল লেখা হয়েছে। এই গুণফল থেকে আরো অনেক গুণফল বাদ দেয়া হয়েছে। বাদ দেয়া গুনফলগুলোতে যেই x এর সমাধান বের করতে হবে সেটি নেই এবং অন্য যেকোনো একটি x নেই। এখন তাহলে একটা সাধারণ সমীকরণ লিখে ফেলা যাক।

সমাধানের ভগ্নাংশে একটা গুণফল দুইবার ব্যবহৃত হয়। এটাকে আমরা z ধরে নিচ্ছি। ফলে,

এখানে ∏ চিহ্নটা আসলে কোনো গুণফলকে সহজভাবে লেখার কাজে ব্যবহার করা হয়। এটা নিয়ে সমস্যা হলে Capital Pi notation নিয়ে আরো পড়তে পারেন।

আর ভগ্নাংশের হরের অন্যান্য পদগুলোকে একসাথে w হিসেবে নামান্বিত করলে,

এখানে Capital-sigma notation ব্যবহৃত হয়েছে। যেহেতু প্রত্যেকটি পদে x_i বাদেও অন্য একটি x বাদ পড়ে, তাই প্রত্যেকটি x দ্বারা আলাদা আলাদাভাবে z কে ভাগ করে শেষে সব ভাগফলগুলোকে যোগ করা হয়েছে।

এখন তাহলে আমাদের কাংখিত সমাধানটা লিখে ফেলি,

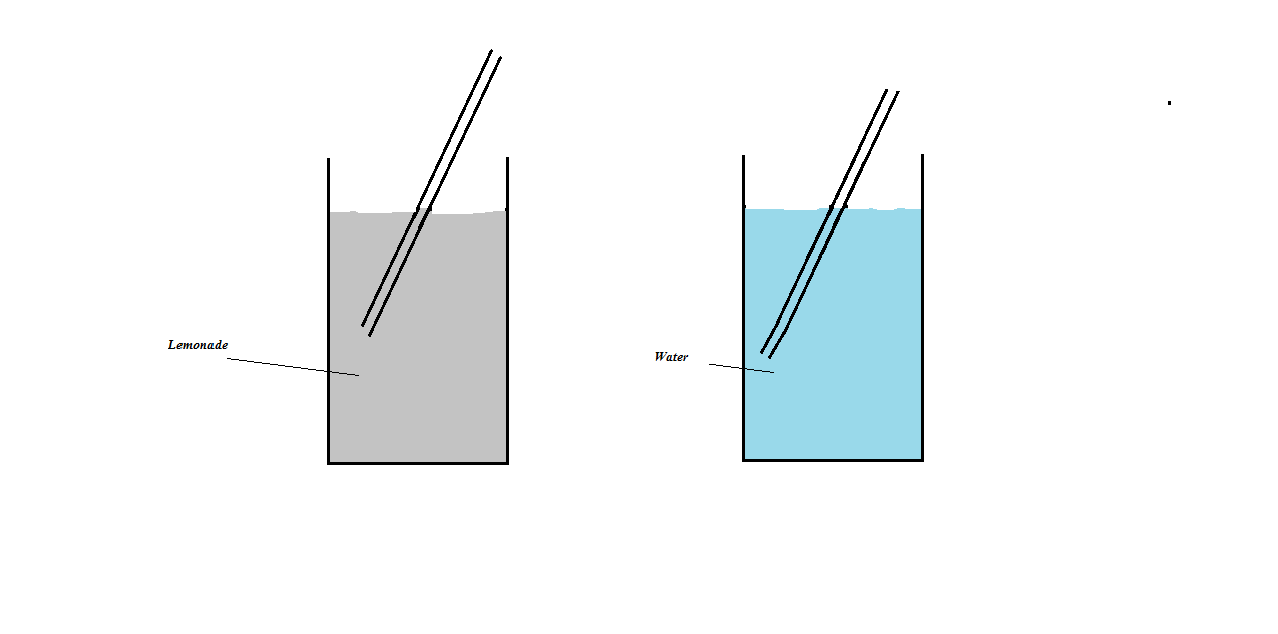
সমস্যা-২: মাউন্টেইন ডিউ এর কাঁচের বোতল হাতে নিয়ে মুন দেখল যে স্ট্র-টির 45% লেমোনেডের ভিতর নিমজ্জিত অবস্থায় আছে। এরপর মুন ঐ স্ট্র-টিকে তুলে এনে পানিভর্তি একটি বোতলে ডুবালো। এবারে দেখা গেল যে, 55% অংশ পানিতে নিমজ্জিত হয়ে আছে। তাহলে, লেমোনেডের ঘনত্ব কত?

সমাধান:

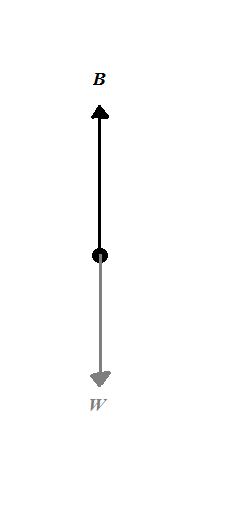
প্রথমেই আমাদেরকে আর্কিমিডিসের নীতি মনে করতে হবে। এ নীতি অনুসারে অপসারিত তরলের সমান ওজনের প্লবতা (upthrust) নিমজ্জিত বস্তুর ওপর উপরের দিকে ক্রিয়া করে। আমরা প্লবতার কারণে অনুভূত বলকে B এবং নিমজ্জিত বস্তুর মোট ওজনকে W দ্বারা প্রকাশ করব।

যেহেতু বস্তুটি ভাসতে থাকে তাই এর ওপর ক্রিয়ারত মোট বল শূন্য। তাহলে,

স্ট্র-টির ঘনত্বকে আমরা ρ_s দ্বারা চিহ্নিত করব। এখন ধরে নেই যে, স্ট্র-টির মোট আয়তন V_s । আর, স্ট্র-টি লেমোনেডের যে পরিমাণ আয়তন অপসারণ করেছে তাকে V_l দ্বারা চিহ্নিত করি। তাহলে,

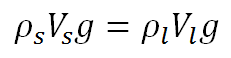(কারণ, ভর হচ্ছে আয়তন ও ঘনত্বের গুণফল)

যেহেতু, স্ট্র-এর 45% লেমোনেডে ডুবে আছে তাই V_l হবে V_s এর 45% । আর তাই,

 ফলে,

…(1)

এখন, আমরা পানি ও স্ট্র- এই ব্যাপারটি থেকে আরেকটি সমীকরণ উদ্ধার করার চেষ্টা করব। এক্ষেত্রেও,

পানির ঘনত্ব ρ_w এবং স্ট্র দ্বারা পানির অপসারিত অংশের আয়তন যদি V_w হয় তাহলে,

এবারে V_w হচ্ছে V_s এর 55% । আর তাই,

(1) সমীকরণে এই মান বসিয়ে দিলে পাব,

বা,

সমস্যা-৩: একটি কক্ষে N জন (N>3) মানুষ আছে। এদের মধ্যে কমপক্ষে একজন সবার সাথে হ্যান্ডশেক করেনি। তাহলে, সবার সাথে হ্যান্ডশেক করেছে এমন মানুষের সংখ্যা সর্বোচ্চ কত হতে পারে?

সমাধান: প্রথমে আমরা সবাইকে A₁, A₂,… ও A_N দ্বারা চিহ্নিত করি। সমস্যায় বলা হয়েছে যে কমপক্ষে একজন সবার সাথে হ্যান্ডশেক করেনি। ধরে নিই যে A₁ সবার সাথে হ্যান্ডশেক করেনি। যেহেতু আমাদেরকে ‘সবার সাথে হ্যান্ডশেক করেছে’ এমন মানুষের সর্বোচ্চ  সংখ্যা বের করতে হবে তাই আমাদেরকে A₁ সর্বোচ্চ কতগুলো হ্যান্ডশেক করতে পারে তার হিসাব কষতে হবে। ধরে নেই যে সে একজনের সাথে হ্যান্ডশেক করেনি এবং সেই ব্যক্তিটি A₂ । তাহলে, বুঝা গেল যে A₁ ও A₂ সর্বোচ্চ (N−1) জনের সাথে হ্যান্ডশেক করতে পারবে। কিন্তু, A₁ ও A₂ বাদে বাকি (N−2) জন কিন্তু ঠিকই সবার সাথে হ্যান্ডশেক করতে পারে। তাহলে, সবার সাথে হ্যান্ডশেক করেছে এমন মানুষের সর্বোচ্চ সংখ্যা হতে পারে (N−2) ।

সমস্যা-৪: x+3y+6z=0 এটা কিসের সমীকরণ?
a) সরলরেখা (line);
b) গোলক (sphere);
c) তল (plane)?

সমাধান: 

ত্রিমাত্রিক স্থানাংক ব্যবস্থায় A(1,2,3) বিন্দুটির কথা আমরা চিন্তা করছি। তাহলে,

(সমস্যা হলে ভেক্টরের Ordered set notation দেখে নিতে পার। সহজ কথায় এই ভেক্টরটির X-অক্ষ বরাবর উপাংশ 1, Y বরাবর 2 এবং Z বরাবর 3 ।)

এখন আমরা যেকোনো একটি ভেক্টর P এর কথা চিন্তা করব যেখানে,

এই দুটি ভেক্টরের Dot product আমাদের নিতে হবে।

কিন্তু, বলে দেয়া ছিল যে, x+3y+6z=0 । ফলে,

এখন, আমরা যা লিখতে পারি তা হচ্ছে,

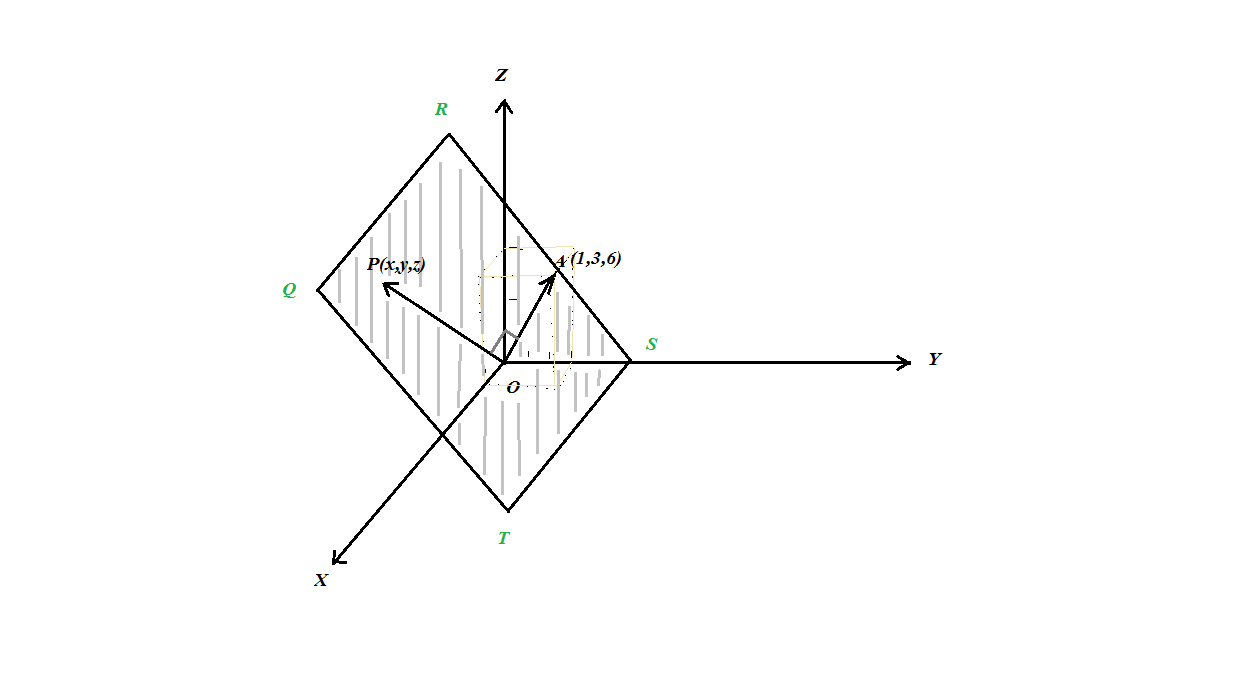
অর্থাৎ, P সবসময়ই OA এর লম্ব হবে। এখন, কোনো একটি ভেক্টরের লম্ব আরেকটি ভেক্টর একটি তল দিয়েই আঁকা সম্ভব।

চিত্রে QRST দ্বারা OA এর লম্ব একটি তল বুঝানো হয়েছে। P ভেক্টরটি এই তলেই অবস্থিত। তার মানে, P এর বিভিন্ন মানের জন্য আমরা একই তলে ভিন্ন ভিন্ন বিন্দু পাব। আর তাই, x+3y+6z=0 সমীকরণটি একটি তলের সমীকরণ।