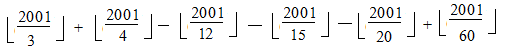সমস্যা-১: 2001 এর চেয়ে বড় নয় এমন কতগুলো ধনাত্মক পূর্ণসংখ্যা আছে যারা 3 বা 4 এর গুণিতক, কিন্তু 5 এর গুণিতক নয়?
সমাধান: প্রথমে আমরা 3 এবং 4 এর যতগুলো গুণিতক আছে সেগুলো খুঁজে বের করব। গুণিতক বের করার আগে আমাদের Floor and ceiling functions সম্পর্কে ধারণা নিতে হবে। আপাতত আমি Floor function আবছাভাবে কভার করছি। নিচের সমীকরণটি দেখ,
অর্থাৎ, আমরা যদি কোনো সংখ্যার ওপর Floor function প্রয়োগ করি তাহলে দশমিকের পর যা আছে তা সব বাদ হয়ে যাবে। দশমিকের পর কি আছে বা নেই তা আমাদের বিবেচ্য বিষয় না। এখন যেহেতু আমরা Floor function শিখে ফেলেছি তাই এটা ব্যবহার করে সহজেই গুনিতকের সংখ্যা বের করা যাবে। যেমন, 2001 পর্যন্ত 3 এর গুনিতক থাকবে 
টি, 4 ও 12 এর গুণিতক থাকবে যথাক্রমে 
ও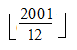 
টি। তোমরা হয়তো চিন্তা করছ আমি 12 এর গুণিতক হিসেব করেছি কেন? কারণ, আমরা যখন 3 ও 4 এর গুণিতক নিয়ে চিন্তা করছি তখন এদের সাধারণ উৎপাদক দুইবার করে গণনা করা হচ্ছে। যেমন, 12, 24, 36- এরা একই সাথে 3 ও 4 এর গুণিতক। ফলে, আমরা যখন 3 ও 4 এর মোট গুণিতক হিসেব করব তখন দুইবার গণনা করা সংখ্যাগুলো একবার বাদ দিতে হবে। তাই, 3 ও 4 এর মোট গুণিতকের সংখ্যা দাঁড়াচ্ছে,
আমাদের কাজ এখনো শেষ হয়নি। 5 এর গুণিতক হওয়া যাবে না- এই শর্তটা কিন্তু আমরা এখনো বিবেচনায় আনিনি। 5 এর গুণিতক এমন সংখ্যাগুলোকে আমাদের হিসেব করে বাদ দিতে হবে। 3 ও 5 এর সাধারণ বা কমন গুণিতকগুলো কিন্তু আমরা গুণে ফেলেছি। একই সাথে 3 ও 5 এর গুণিতক হতে হলে 15 এরও গুনিতক হতে হবে। আবার, 4 ও 5 এর সাধারণ গুণিতক হতে হলে 20 এরও গুণিতক হতে হয়। ফলে,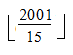 
ও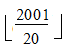 
– এতগুলো সংখ্যা আমরা অতিরিক্ত সংখ্যা গণনা করেছি। ফলে, 
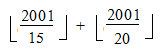এতগুলো সংখ্যা বাদ দিতে হয়! কিন্তু, আরেকটু কাজ বাকি আছে! এখানেও 15 ও 20 এর সাধারণ গুণিতকগুলো দুইবার কাউন্ট করা হয়েছে। 15 ও 20 এর গুণিতকগুলো আবার 60 এরও গুণিতক। ফলে, আমাদের আসলে যা বাদ দিতে হবে তা হল 
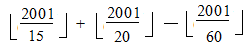। ফলে, 3 ও 4 এর গুণিতক, কিন্তু 5 এর গুণিতক নয় এমন সংখ্যা দাঁড়ায়,
এখন ক্যালকুলেটর টিপলেই কাজ শেষ। আর, উত্তর পাবে 801 ।
সমস্যা-২: একটি মাকড়সার আটটি পায়ের প্রত্যেকটির জন্য একটি করে মোজা ও জুতা বরাদ্দ আছে। মাকড়সাটি কত উপায়ে এগুলো পরতে পারে? (যেকোনো একটি পায়ের মোজা পরার পরই কেবল সেই পায়ের জুতা পরা যাবে, তার আগে নয়!)
সমাধান: প্রথমে মাকড়সাটির পাগুলোকে 1 থেকে 8 পর্যন্ত সংখ্যাগুলো দ্বারা চিহ্নিত করি। এখন আমরা মোজাগুলোকে a1,a2,…,a8 দ্বারা এবং জুতাগুলোকে b1,b2,…,b8 দ্বারা চিহ্নিত করব। মোজা এবং জুতাগুলো নাম্বার অনুসারে একেক পায়ে যাবে। এখন a1,a2,…,a8 এবং b1,b2,…,b8 এই 16 টি আমরা 16! উপায়ে একটি শব্দ হিসেবে সাজাতে পারি। শব্দে যেটি আগে আসবে সেটি আগে পায়ে যাবে। কিন্তু, আরেকটি শর্ত আছে! সেটি হল যে, মোজার আগে জুতা পরা যাবে না। অর্থাৎ, আমাদের তৈরি করা শব্দে a1 এর আগে b1 আসতে পারবে না। কিন্তু, 16! শব্দের মাত্র অর্ধেকটিতে b1 এর আগে a1 আসবে। (কারণ, নির্দিষ্ট দুটি ঘরের মধ্যে দুটি ভিন্ন উপাদান 2! বা 2 উপায়ে বিন্যস্ত হতে পারে।) ফলে, আপাতভাবে কাঙ্ক্ষিত উপায়ের সংখ্যা দাঁড়াবে 16!/2 টি। কিন্তু, তাতে কিন্তু উত্তর মিলবে না। কেননা, আমরা মাত্র b1 ও a1 এর ক্ষেত্রে এটি ব্যবহার করেছি। বাকি আট জোড়ার ক্ষেত্রেও এই নিয়ম ব্যবহার করতে হয়। ফলে, উপায় হবে 16!/28 টি।
সমস্যা-৩: ধরি, x=0.123456789101112…997998999,
যেখানে 1 থেকে 999 পর্যন্ত সবগুলো পূর্ণসংখ্যা ব্যবহার করে x এর ডিজিটগুলো লেখা হয়েছে।
তাহলে দশমিকের ডান দিকের 1887 তম ডিজিটটা কি?
সমাধান: 123456789- এখানে ডিজিট আছে 9 টি। 101112…9899- এখানে 90 টি পূর্ণ সংখ্যা লিখা হয়েছে এবং এরা 90×2=180 টি ডিজিট দখল করে আছে। ফলে, এক এবং দুই অংক বিশিষ্ট সংখ্যাগুলো 189 টি ডিজিট কন্ট্রিবিউট করেছে। আমাদের জানা প্রয়োজন 1887 তম ডিজিটটি কি? 100101102…998999 এক্ষেত্রে সবগুলোই তিন অংকবিশিষ্ট। (1887-189)=1698 টি ডিজিট দখল করে থাকবে তিন অঙ্কবিশিষ্ট সংখ্যাগুলো। এক্ষেত্রে প্রথম পূর্ণ সংখ্যাটি 100। ফলে, 1698/3=566 তম পূর্ণ সংখ্যাটি হবে (100+566-1)=665 । আর তাই, 1887 তম ডিজিটটি হবে 5 ।
সমস্যা-৪: প্রথম 18 টি ধনাত্মক পূর্ণসংখ্যা থেকে যেকোনো 5 টি সংখ্যা কতভাবে বাছাই করা যায় যাতে যেকোনো দুটি বাছাইকৃত সংখ্যার পার্থক্য কমপক্ষে 2 হয়?
সমাধান: ধরা যাক, বেছে নেয়া সংখ্যাগুলো হল <a1, a2, a3, a4, a5> । এখন আমাদের একটু ভিন্নভাবে চিন্তা করতে হবে।
ধরে নিই, <b1,b2,b3,b4,b5>=<a1, a2-1, a3-2, a4-3, a5-4> ।
এখানে, আমাদের সমস্যাটা একটু ভিন্ন তো হলই, সেই সাথে অনেক সহজও হয়ে গেল। যেমন, আমরা <10,12,16,14,18> এই উপায়টাকে <10,11,12,13,14> তে রূপান্তর করে ফেলেছি। এভাবে প্রত্যেক কাঙ্ক্ষিত সমাধানকে আমরা প্রথম 14 টি পূর্ণ সংখ্যা থেকে বেছে নেয়া 5 টি পূর্ণ সংখ্যার গ্রুপের সাথে রিলেট করেছি (একে Correspondence ও বলে)। এখন 14 টি থেকে 5 টি কত উপায়ে বাছা যায় তা জানলেই কাজ শেষ। অর্থাৎ, সমাধান হল 14C5 ।
সমস্যা-৫: পাশাপাশি 9 টি সিট রাখা আছে। 6 জন ছাত্র প্রতিনিধি এবং প্রফেসর কবির, সামিনা ও ইকবাল এখানে বসবেন। প্রথমেই প্রফেসর তিনজন বসার সুযোগ পাবেন এবং এমনভাবে বসবেন যাতে তাদের প্রত্যেকের দুপাশে দুজন ছাত্র প্রতিনিধি বসতে পারে। প্রফেসররা কতভাবে এই বসার কাজটি সম্পাদন করতে পারেন?
সমাধান: প্রশ্ন থেকে সরাসরিই বুঝা যাচ্ছে যে দুই প্রান্তের দুটি সিটে প্রফেসররা বসবেন না। বাকি থাকল 7 টি সিট। এখন, যেকোনো দুইজন প্রফেসর পাশাপাশি বসতে পারবেন না। “সমস্যা-৪” এ আমরা 18 টি সংখ্যা থেকে 5 টি এমনভাবে বেছেছি যাতে পাশাপাশি দুটি সংখ্যা না থাকে। এখানে 7 টি থেকে 3 টি এমনভাবে বাছতে হবে যাতে পাশাপাশি যেকোনো দুটি বাছা না হয়। ভিন্নভাবে বলা যায় যে, 5 টি থেকে 3 টি বাছতে হবে। (এখানে, কিন্তু ‘পাশাপাশি দুটি বাছা যাবে না’- এই শর্তটা আর থাকল না!) তবে, আরেকটি বিষয় বিবেচনায় রাখতে হয়। এখানে, প্রফেসরদের ক্রমও কিন্তু বিবেচনায় আসবে। ফলে, আমাদের বিন্যাস নিতে হবে, সমাবেশ নয়। সুতরাং, উত্তর হবে 5P3 বা 60 ।
ATM Jahid Hasan
Latest posts by ATM Jahid Hasan (see all)
- আজ আমি বৃষ্টি দেখেছি! - February 2, 2016
- কুইজ :: Nov 2015; Week 2 - November 29, 2015
- কুইজ :: Nov 2015; Week 1 - November 12, 2015