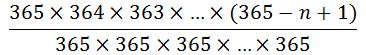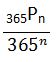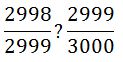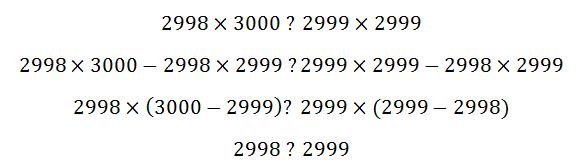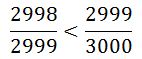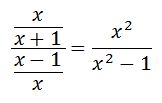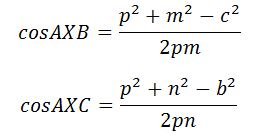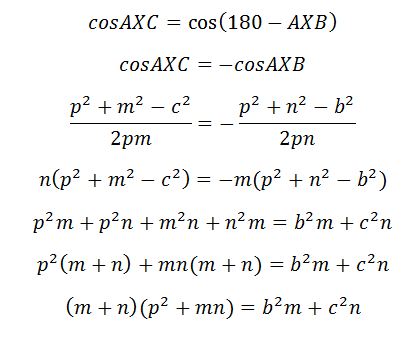অগাস্ট তৃতীয় সপ্তাহের কুইজের সমাধান

সমস্যা-১: একদল মানুষের মধ্যে ন্যূনতমপক্ষে দুইজনের জন্মদিন একই দিনে হওয়ার সম্ভাবনা 60% এর বেশি হতে হলে সেই দলটিতে কমপক্ষে কতজন মানুষ থাকতে হবে?

সমাধান: আমাদের যা করতে বলা হয়েছে তা হল ন্যূনতমপক্ষে দুইজনের জন্মদিন একই দিনে হওয়ার সম্ভাবনা বের করা। তার মানে, দুইজনের বেশি মানুষের একই দিনে জন্মদিন হওয়ার সম্ভাবনাও কিন্তু এর আওতাভুক্ত। তাই আমাদের একটু অন্যপথে এই সম্ভাবনা হিসাব করতে হবে। প্রথমে আমরা কারো জন্মদিনই একই দিনে পরে না এমন সম্ভাবনা হিসাব করব। তারপর 1 থেকে তা বিয়োগ দিলেই পাওয়া যাবে আমাদের কাঙ্ক্ষিত সম্ভাবনা।

ধরি, কারো জন্মদিন একই দিনে না হওয়ার সম্ভাবনা P’ । তাহলে, ন্যূনতমপক্ষে দুইজনের জন্মদিন একই দিনে হওয়ার সম্ভাবনাকে P দ্বারা চিহ্নিত করলে, P=1−P’ । তাহলে, এখন P’ এর মান বের করা যাক! দলভুক্ত মানুষগুলো থেকে প্রথম যে জনকে বেছে নিব তার জন্মদিন বছরের যেকোনো একদিনে হওয়ার সম্ভাবনা 365/365 । বেছে নেয়া দ্বিতীয়জনের জন্মদিন কিন্তু প্রথমজনের জন্মদিনের সাথে মিলতে পারবে না। তাই তার জন্য অবশিষ্ট থাকল 364 দিন। অর্থাৎ, তার জন্মদিন ভিন্ন হওয়ার সম্ভাবনা দাঁড়াল 364/365 । তৃতীয়জনের জন্মদিন হতে হবে বাকি 363 দিনের যেকোনো একদিনে। ফলে, তার জন্মদিন ভিন্ন হওয়ার সম্ভাবনা 363/365 । এভাবে মানুষ যত বাড়বে ভিন্ন ভিন্ন জন্মদিন হওয়ার সম্ভাবনা ততই কমতে থাকবে। এখন Product Rule ব্যবহার করলে n জনের জন্মদিন ভিন্ন হওয়ার সম্ভাবনা দাঁড়াবে,

এখন এই ভগ্নাংশকে নিম্নোক্ত উপায়েও লেখা যায়।

₃₆₅P_n কিভাবে আসল তা জানার জন্য হাবিজাবি ১.১ এ চোখ বুলানো যেতে পারে। এখন n এর মান বসিয়ে আমাদের দেখতে হবে n এর কোন মানের জন্য P’ এর মান 40% এর কম আসে। একমাত্র n এর সেই মান তদপরবর্তী প্রত্যেক মানের জন্য P এর মান 60% এর বেশি আসবে। n এর মান 26 বসালে আমরা দেখি যে P’ এর মান আসে 40.175%। কিন্তু এতে P এর মান 60% এর নিচে নেমে যাবে। আবার n এর মান 27 বসালে দেখব যে P’ এর মান আসে 37.314%। এবং এই ক্ষেত্রে P এর মান আসে 62.686%। অর্থাৎ, দলটিতে মানুষের সংখ্যা হতে হবে কমপক্ষে 27 জন।

সমস্যা-২: ক্যালকুলেটর ব্যবহার না করে বের কর নিচের কোনটি বড়- 2998/2999 নাকি 2999/3000?

সমাধান: প্রথমে ভগ্নাংশ দুটি পাশাপাশি লিখি আর মাঝে ? চিহ্ন দেই।

2999×3000 দিয়ে গুণ করে ফেলি,

উপরের লাইনটি দেখে বুঝা যাচ্ছে যে ? এর জায়গায় < চিহ্নটি বসবে। কেননা,

ফলে,

এই সমস্যাটির সমাধান আরো অনেক উপায়েই করা যায়। এদের মধ্যে একটা সমাধান এখানে উল্লেখ করা প্রয়োজন।

ধরি, x=2999। তাহলে প্রথম সংখ্যাটি দাঁড়াবে (x-1)/x আর দ্বিতীয় সংখ্যাটি x/(x+1)। দ্বিতীয় সংখ্যাটিকে প্রথম সংখ্যাটি দ্বারা ভাগ করি।

স্পষ্টতই সমীকরণের ডান পাশ 1 এর চেয়ে বড়। আর তাই দ্বিতীয় সংখ্যাটি প্রথমটির চেয়ে বড়। একই কারণে 1998/1999 এর চেয়ে 1999/3000 বড়, 3998/3999 এর চেয়ে 3999/4000 বড়!

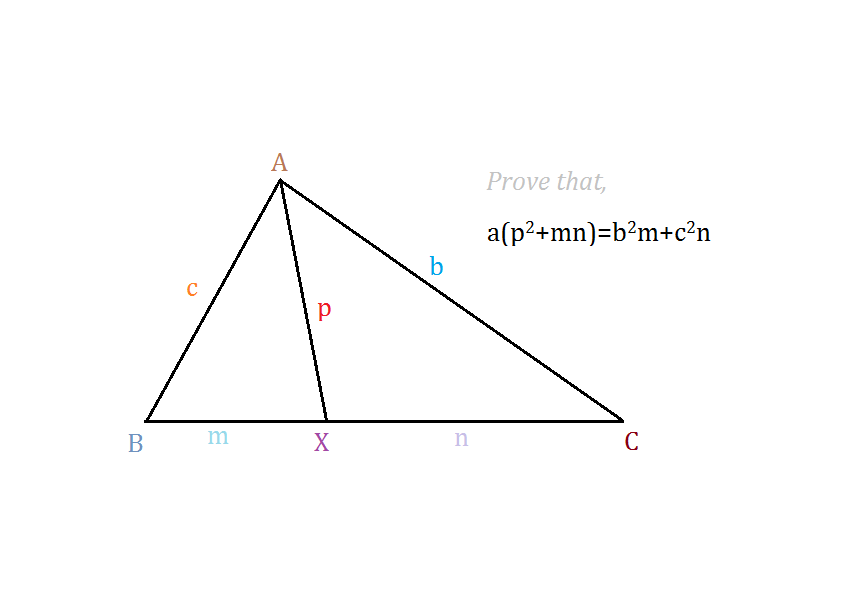
সমস্যা-৩: ত্রিভুজ ABC তে A বিন্দু থেকে BC বাহুর যেকোনো একটি বিন্দু X পর্যন্ত রেখা টানা হল। যদি AX=p, BX=m, XC=n, BC=a, AC=b ও AB=c হয়, তাহলে প্রমাণ কর যে,

সমাধান: কোণ AXB আর AXC এর ক্ষেত্রে কোসাইন রুল এপ্লাই করলেই কেল্লা ফতে। তাহলে, এপ্লাই করা যাক!

কিন্তু,

আবার, m+n=a হওয়ায়,

এটি Stewart’s theorem নামে পরিচিত স্কটিশ গণিতবিদ Matthew Stewart 1746 সালে প্রকাশ করেন।

সমস্যা-৪: 1,2,3,4 দ্বারা যতগুলো চার অংকের সংখ্যা (সংখ্যাগুলোতে কোনো অংকের পুনরাবৃত্তি হতে পারবে না) লেখা যায় তাদের যোগফল কত?

সমাধান: 1, 2, 3, 4 দ্বারা 4! টি সংখ্যা লেখা যায় যেখানে কোনো অংক পুনরাবৃত্তি করা হয় না। এখন 4! বা 24 টি সংখ্যাগুলোর মধ্যে এককের ঘরের অংকটি 1, 2, 3, 4 এর মধ্যে যেকোনো একটি হতে পারে। এককের ঘরটি পূরণ করার চারটি উপায় থাকায় 24 টি সংখ্যার মধ্যে 6 টিতে এককের ঘরে 1, 6 টিতে এককের ঘরে 2, 6 টিতে এককের ঘরে 3 এবং 6 টিতে এককের ঘরে 4 থাকবে। ফলে, এককের ঘরের অংকগুলোর কারণে যোগফল হবে,

একইভাবে দশক, শতক ও হাজারের ঘরের অংকগুলোর হিসাবও আমরা করতে পারি। এই কারণে মোট যোগফল,

সমস্যা-৫: অনি, বনি, গিনি আর ডিনি পাশাপাশি চারটি চেয়ারে বসবে। শর্ত জুড়ে দেয়া হল যে, অনি ও গিনি পাশাপাশি বসবে এবং ডিনি বসবে অনি বা গিনির পাশে। তাহলে, এই চারজন কত উপায়ে বসতে পারে?

সমাধান: প্রশ্ন দেখেই বুঝা যাচ্ছে যে, বনিকে যেকোনো এক প্রান্তে বসতে হবে। আর, অনি, গিনি আর ডিনির যেই বিন্যাসগুলো সম্ভব সেগুলো হল, (অনি, গিনি, ডিনি), (গিনি, অনি,ডিনি), (ডিনি, অনি, গিনি) ও (ডিনি, গিনি, অনি)। আর এই প্রত্যেকটা বিন্যাসের দুই প্রান্তের যেকোনো এক প্রান্তে বনিকে বসিয়ে দিলেই কাজ শেষ। ফলে, মোট উপায় 2+2+2+2=8 ।