হাবিজাবি ১.১ এর একদম শেষে Product Rule নিয়ে লিখেছিলাম। প্রথমে ভেবেছিলাম শুধু সংজ্ঞা দেয়াই যথেষ্ট হবে, কিন্তু এখন মনে হচ্ছে একটু ব্যাখ্যার প্রয়োজন আছে। ব্যাখ্যার আগে তাই আবার Product Rule কাকে বলে তা উল্লেখ করছি-
Product Rule: যদি k length এর কোনো string এর ক্ষেত্রে i তম পদটি ni উপায়ে পূরণ করা যায় তাহলে, তাহলে মোট সম্ভাব্য string এর সংখ্যা হবে n1n2n3…nk ।
(i এর মান এখানে 1 থেকে k পর্যন্ত হতে পারে। আর, i তম পদ কত উপায়ে পূরণ করা যায় তা কিন্তু পূর্ববর্তী কোনো পদ কিভাবে পূরণ করা হয়েছে তার উপর নির্ভরশীল হতে পারবে না।)
ধরা যাক, MATRIX শব্দটির পুনর্বিন্যাস আমাদের নির্ণয় করতে হবে। Product Rule ব্যবহার করে আমরা সহজেই বলে দিতে পারি যে পুনর্বিন্যাসের সংখ্যা হবে 6! (MATRIX শব্দটি সহ)। কিন্তু আমাদের যদি বলা হয় যে এমন পুনর্বিন্যাসের সংখ্যা বের করতে হবে যেখানে শেষে অবশ্যই A, T অথবা M বসতে হবে, তাহলে কি আমরা আগের মত Product Rule ব্যবহার করতে পারব? না। কারণ এবারে শেষ জায়গাটি কতভাবে পূরণ করা যাবে তা আগের জায়গাগুলো কিভাবে পূরণ করা হয়েছে তার ওপর নির্ভর করবে! আমরা যদি শেষ খালিঘরটিতে পৌঁছানোর আগেই A, T ও M বর্ণগুলো ব্যবহার করে ফেলি তাহলে কিন্তু পূরণ করার জন্য কোনো বর্ণ অবশিষ্ট থাকছে না। এ কারণে Product Rule আমাদের কোনো কাজে আসছে না। এখন প্রশ্ন আসতেই পারে যে সমস্যার সমাধান তাহলে কিভাবে হবে? এক্ষেত্রে আমরা একটা ট্রিক ব্যবহার করতে পারি। আমরা উল্টো করে Product Rule করব। মানে, শেষ জায়গাটি প্রথমেই বর্ণ দিয়ে পূরণ করে ফেলব। শেষ জায়গাটি A, T অথবা M দিয়ে পূরণ করা যায়। শেষ জায়গাটি ভরাট হওয়ার পর পঞ্চম জায়গাটি পূরণ করা যাবে বাকি 5 টি বর্ণ দিয়ে এবং 5 উপায়ে, চতুর্থটি 4 উপায়ে, …, এভাবে প্রথমটি মাত্র 1 উপায়ে। ফলে, শর্তাধীন পুনর্বিন্যাস সংখ্যা দাঁড়াবে 1×2×3×4×5×3 টি। এখানে আমরা উল্টো দিক দিয়ে Product Rule প্রয়োগ করতে পেরেছি কারণ উল্টো দিক দিয়ে পূরণ করার সময় আগে পূরণকৃত জায়গাটি কিভাবে পূরণ করা হয়েছে তার ওপর ভিত্তি করে পরে বিবেচনায় আসা জায়গাগুলো পূরণের উপায় সংখ্যা পরিবর্তিত হয়নি। যদি, শেষ জায়গাটি কিভাবে পূরণ করতে হবে তা নির্ধারণ করে না দিয়ে মধ্যবর্তী কোনো জায়গা কিভাবে পূরণ করতে হবে তার ব্যাপারে শর্ত জুড়ে দেয়া হত তাহলে হিসাব জটিল হত। কেননা তখন উল্টো দিক দিয়েও Product Rule ব্যবহার করা যেত না। এসব ক্ষেত্রে তাই আমাদের অন্য রাস্তা খুঁজতে হয়!
এখন আমরা Probability তে ডুব দিব। সম্ভাব্যতা, সম্ভাবনা, Probability – এই শব্দগুলো আমরা একই অর্থে ব্যবহার করি সাধারণত। বাস্তব জীবনের সম্ভাবনাগুলোকে আরো জাগতিক রূপ দেয়ার জন্য গণিতে আমরা সম্ভাব্যতা টেনে নিয়ে আসি। সর্বপ্রথম ফার্মা তাসের খেলাতে সম্ভাবনার হিসাব করতে গিয়ে গণিতে এই বিষয়টির সূচনা করেন। প্রথমে আমরা সম্ভাবনা বা সম্ভাব্যতা বা Probability এর সংজ্ঞা জেনে নিব।
Probability: যদি কোনো একটা ঘটনা m সংখ্যক সমসম্ভাব্য উপায়ে (equally likely ways) ঘটতে পারে এবং সেই উপায়গুলোর মধ্যে n সংখ্যক উপায় একটা নির্দিষ্ট শর্ত পূরণ করে তাহলে, সেই শর্ত পূরণ হওয়ার সম্ভাবনা n/m ।
একটা জিনিস লক্ষ্য করা উচিত! আমি লিখেছি যে ‘m সংখ্যক সমসম্ভাব্য উপায়’। সম্ভাবনার সংজ্ঞা দিতে গিয়ে আমিই আবার ‘সমসম্ভাব্য’ শব্দটি ব্যবহার করেছি! এটা আসলে এক ধরণের লুপহোল! সমসম্ভাব্য ঘটনা বলতে আমরা সেসব ঘটনাগুলোকে বুঝাব যাদের ঘটনসংখ্যা সমান। এই ব্যাপারটা এখন না বুঝলেও সমস্যা নেই। ‘সমসম্ভাব্য’ ব্যাপারটা তখনই পরিষ্কার হবে যখন এটি মাথায় রেখে আমাদের সম্ভাবনা গুণতে হবে। আপাতত আমরা সাধারণ সম্ভাবনার ওপর আলোকপাত করতে চাই।
ধরে নেয়া যাক, আমাদের কাছে একটা পয়সা আছে!(সবচেয়ে সোজা উদাহরণ।) যখন এটা আমরা উপরে ছুঁড়ে মারব তখন দুটি ঘটনা ঘটতে পারে। হয় Head অথবা Tail আমরা দেখতে পারব। তার মানে এখানে m হচ্ছে 2 । যদি বলা হয় Head উঠার সম্ভাবনা বের কর তাহলে, প্রথমেই আমাদের n এর মান বের করতে হবে। এখানে Head পাওয়ার ঘটনাটা মাত্র একবার ঘটছে। তাই এখানে n এর মান 1 । আর তাই সম্ভাবনা হল ½ । একইভাবে Tail পাওয়ার সম্ভাবনাও ½ । এরপর আসা যাক আরেকটু কঠিন হিসাবের দিকে। এবারে আমরা পয়সাটি চারবার উপরে ছুঁড়ে মারব। যদি আমরা Head কে H দ্বারা আর Tail কে T দ্বারা চিহ্নিত করি তাহলে যতগুলো ঘটনা ঘটবে তার সবগুলোকেই আমরা 4-letter word দ্বারা প্রকাশ করতে পারব। তাহলে মোট কতগুলো ঘটনা ঘটতে পারে তা জানার জন্য আমাদের {H, T}-এই সেটের উপাদান ব্যবহার করে 4-length এর কতগুলো string বা word লেখা যায় তা বের করলেই চলবে। এবং, এমন word এর সংখ্যা 2×2×2×2=16 । এখন আমরা যদি দুটি Head উঠার সম্ভাবনা বের করতে চাই তাহলে আমাদের এমন word এর সংখ্যা হিসাব করতে হবে যেখানে কেবল 2 টি Head উঠে। আর এমন word আছে 4C2 বা 6 টি।(এই হিসাব কিভাবে করতে হয় তা হাবিজাবির পরবর্তী সংখ্যাগুলোতে আলোচনা হবে।) ফলে, সম্ভাবনা দাঁড়াবে 6/16 বা 3/8 ।
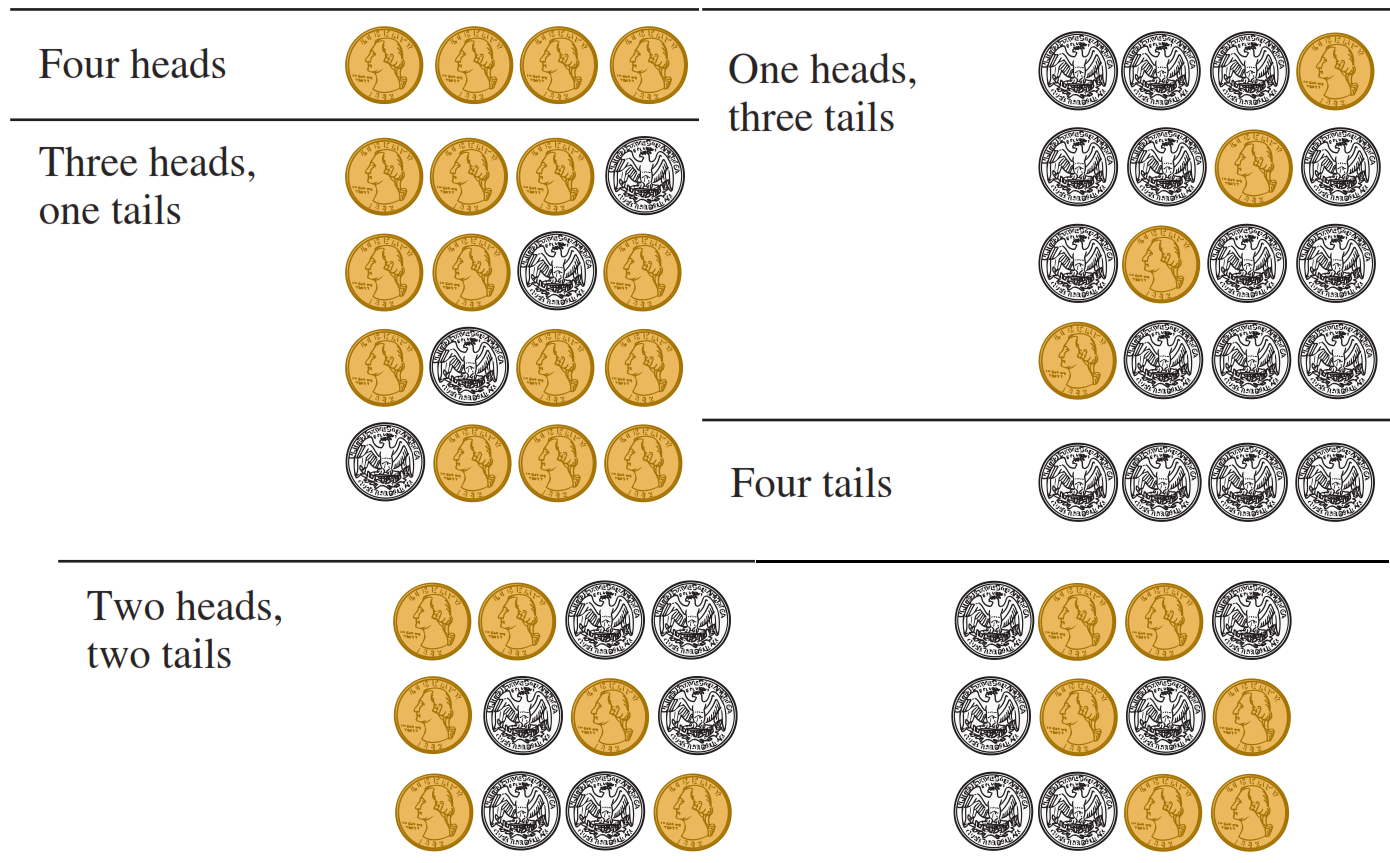
এবার আমরা চারটি পয়সা উপরে ছুঁড়ব। এটির ঘটনাগুলোও কিন্তু আমরা string গুণে বের করতে পারি। এক্ষেত্রেও মোট ঘটনার সংখ্যা 16 । আচ্ছা, এবারেও কি 2 টি Head পাওয়ার সম্ভাবনা 3/8 ? মনে কর, তোমার এক বন্ধুকে এই প্রশ্ন জিজ্ঞেস করায় সে উত্তর দিল, “এখানে পাঁচটি ঘটনা সম্ভব। কোনো Head নাও উঠতে পারে, একটা Head উঠতে পারে, দুইটা উঠতে পারে, তিনটা উঠতে পারে আর চারটা উঠতে পারে। এদের মধ্যে কেবল একটা ঘটনা আমাদের কাঙ্ক্ষিত। আর সেটা হচ্ছে দুইটা হেড পাওয়া। তাই সম্ভাবনা 1/5।” তোমার আরেক বন্ধুকে জিজ্ঞেস করায় সে একটা পয়সা চারবার উপরে ছুঁড়লে যেভাবে সম্ভাবনা হিসাব করতে হয় তার সাথে সাদৃশ্য টেনে বলল যে সম্ভাবনা 3/8। কোনটা সঠিক?
তাই তুমি হয়তো ভেবে ভেবে বের করলে যে পয়সাগুলো যদি একই রকম (Identical) দেখতে হয় তাহলে প্রথম বন্ধুর মত অনুযায়ী সম্ভাবনা হবে 1/5 আর যদি এক রকম দেখতে না হয় (Nonidentical) তাহলে হবে 3/8। এখন তাহলে একটা Thought experiment হয়ে যাক। ধরা যাক, তুমি চারটে একই রকম দেখতে পয়সা নিলে এবং পয়সাগুলোর উপর ইনফ্রারেড ক্যামেরায় ধরা পড়ে এমন কালি দিয়ে 1, 2, 3, 4 লিখলে। ফলে, সাধারণ ক্যামেরা আর আমাদের চোখের জন্য পয়সাগুলো একই রকম থাকল, কিন্তু ইনফ্রারেড ক্যামেরার ক্ষেত্রে ভিন্ন ভিন্ন হয়ে গেল। এই পয়সাগুলো নিয়ে এক্সপেরিমেন্ট করলে তাই আমরা শুধু একটা পদ্ধতিতে বের করা সম্ভাব্যতা অনুযায়ী ফলাফল পাব। আর তাই, অন্য সম্ভাব্যতাটা ভুল হিসেবে গণ্য হবে। তুমি যদি সত্যি সত্যি অনেকবার পয়সাগুলো ছুঁড়ে Head Tail এর হিসাবগুলো লিখে রাখ তাহলে দেখবে যে দুইবার Head উঠে এরকম পরীক্ষণের সংখ্যা মোট পরীক্ষণের সংখ্যার 3/8 গুণ হবে। তার মানে দুইবার Head উঠার সম্ভাবনা দাঁড়াবে 3/8। কিন্তু, তোমার প্রথম বন্ধু যে যুক্তিতে সম্ভাবনা 1/5 বের করেছে সেখানে ভুল কোথায়? লক্ষ্য কর আমি Probability এর সংজ্ঞা দেয়ার সময় ‘সমসম্ভাব্য’ কথাটা উল্লেখ করেছিলাম। তোমার প্রথম বন্ধু যে ঘটনাগুলো নিয়ে কাজ করেছে সেগুলো সমসম্ভাব্য নয়। মানে, কোনো Head না পাওয়া আর দুইটা Head পাওয়া- এই ঘটনা দুটি equally likely নয়। কারণ, কোনো হেড নেই এরকম ঘটনা হতে পারে মাত্র একটা; অন্যদিকে দুটি হেড পাওয়া যায় এমন ঘটনার সংখ্যা 6 টি। আর তাই এভাবে বের করা সম্ভাব্যতাটা ভুল। এরকম আর কি কি ভুল আমরা করি? অনেক সময়ই আমরা বলি যে, যেকোনো কিছু ঘটার সম্ভাবনা ½। কারণ হিসেবে আমরা বলি- ঘটনাটি ঘটতেও পারে, নাও পারে। তাই ঘটনাটি ঘটার সম্ভাবনা হয়ে যায় ½। এখানেও ঠিক আগের মত ভুল হয়েছে। কারণ, সবক্ষেত্রে ‘ঘটনাটি ঘটা’ আর ‘না ঘটা’ এই দুটো সমসম্ভাব্য থাকে না। সম্ভাব্যতা নির্ণয়ের ক্ষেত্রে তাই এটি মাথায় রাখা খুবই গুরুত্বপূর্ণ।
সম্ভাব্যতার কিছু সমস্যা এখন দিয়ে যাব-
- 52 কার্ডের একটা ডেক থেকে randomly চারটা কার্ড বেছে নিলে,
- চারটা Ace পাওয়ার সম্ভাবনা কত?
- সবগুলো ভিন্ন ভিন্ন suit এর হওয়ার সম্ভাবনা কত?
- {A, B, C, D, E} ব্যবহার করে তৈরি করা 4-letter word গুলোর মধ্যে যেকোনো একটা বেছে নিলে,
- তাতে কোনো বর্ণ একবারের বেশি না থাকার সম্ভাবনা কত?
- দুটো পাশাপাশি বর্ণ একই না হওয়ার সম্ভাবনা কত?
পরবর্তী সংখ্যায় থাকবে Arrangement আর Derangement নিয়ে কিছু সমস্যা ও তা সমাধানের উপায় নিয়ে কিছু কথাবার্তা।
ATM Jahid Hasan
Latest posts by ATM Jahid Hasan (see all)
- আজ আমি বৃষ্টি দেখেছি! - February 2, 2016
- কুইজ :: Nov 2015; Week 2 - November 29, 2015
- কুইজ :: Nov 2015; Week 1 - November 12, 2015