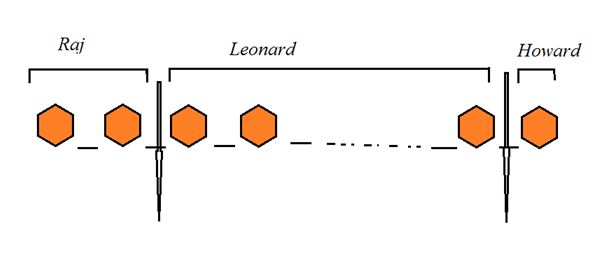
সমস্যা – ১ : Sheldon Cooper এর কাছে 100 টি Juzt Jelly আছে। সে এগুলো Raj, Leonard ও Howard এর মধ্যে এমনভাবে বণ্টন করতে চায় যেন প্রত্যেকে কমপক্ষে একটি Juzt Jelly পায়। Sheldon Cooper এই কাজটি কত উপায়ে সম্পন্ন করতে পারবে?
সমাধান : Sheldon Cooper এর কাছে যেই Juzt Jelly গুলো আছে সেগুলো সমজাতীয় (Identical)। প্রথমে আমরা এই জেলিগুলোকে একটি সারিতে সাজাই। যদি সাজানোর সময় আমরা এদেরকে পরস্পর থেকে সামান্য দূরে দূরে রাখি তাহলে এদের মধ্যবর্তী ফাঁকা স্থান হবে 99 টি। এখন, এই 99 টি খালি বা ফাঁকা স্থান থেকে আমরা যেকোনো দুইটি জায়গা বেছে নিব যেখানে আমরা দুটি কলম বসাব। এতে জেলিগুলো তিনটি ভাগে ভাগ হয়ে যাবে।
এখন, এই তিনটি ভাগ Raj, Leonard আর Howard কে দিয়ে দিলেই আমাদের বণ্টনকার্য শেষ হয়ে যাবে! তাহলে মূল প্রশ্নটি রূপান্তরিত হয়ে দাঁড়াল যে, “99 টি জায়গা থেকে যেকোনো 2 টি জায়গা কতভাবে বেছে নেয়া যায় ?” এর উত্তর হচ্ছে 99C2 । এটাই প্রথম কুইজের উত্তর।
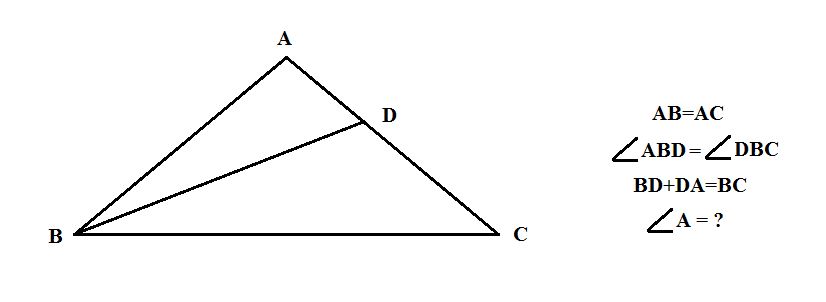
সমস্যা – ২ : ত্রিভুজ ABC তে AB=AC এবং কোণ ABD= কোণ DBC । আরো বলে দেয়া আছে, BD+DA=BC । তাহলে, কোণ A এর মান কত?
সমাধান :
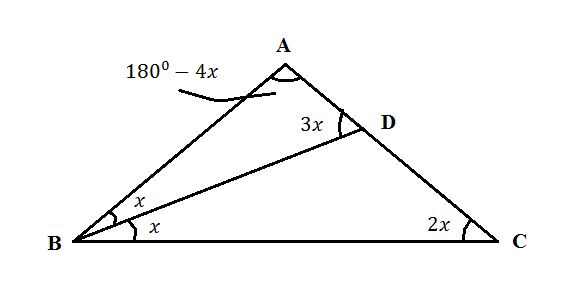
এই সমস্যা সমাধানের জন্য আমাদের ত্রিভুজের সাইন রুল (sine rule) প্রয়োগ করতে হবে। প্রথমে আমরা সাইন রুল প্রয়োগ করব ত্রিভুজ ABD তে। এক্ষেত্রে আমরা যা পাব তা হচ্ছে,
তারপর, আমাদের ত্রিভুজ ABC তে সাইন রুল খাটাতে হবে। এক্ষেত্রে,
এখন, BD+DA=BC সমীকরণটিকে আমরা AB দ্বারা ভাগ করব। ফলে, আমাদের সমীকরণের প্রত্যেকটি পদকে আমরা সাইন ফাংশনের অনুপাতগুলো দ্বারা প্রতিস্থাপন করতে পারব।
এখন এই ত্রিকোণমিতিক সমীকরণ সমাধান করে আমাদের x এর মান বের করতে হবে।
এখন আমাদের উপরের সমীকরণটি সমাধান করতে হবে। আমরা সাইন সমীকরণের সাধারণ সমাধান ব্যবহার করব এক্ষেত্রে। আমরা তিনটি উত্তর পাব যা হচ্ছে,
এই তিনটির মধ্যে মাত্র একটি গ্রহণযোগ্য। সেটি হচ্ছে দ্বিতীয়টি। দ্বিতীয়টি থেকে আমরা যা পাব তা হল,
ফলে, কোণ A দাঁড়াবে,
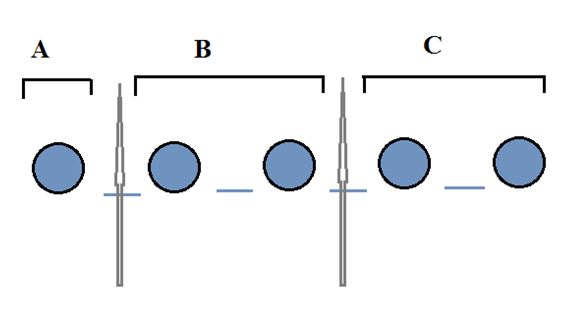
সমস্যা – ৩ : ধরা যাক, তোমার কাছে 5টি সমজাতীয় (identical) বল আছে যেগুলোকে তিনটি বক্স A, B ও C তে এমনভবে রাখতে হবে যেন কোনো বক্স খালি না থাকে। এই কাজটি তুমি কত সংখ্যক উপায়ে করতে পারবে?
সমাধান : আসলে, সমস্যা–১ আর সমস্যা-৩ একই। প্রথম সমস্যায় ব্যবহৃত Juzt Jelly গুলো এই সমস্যার বল আর Raj, Leonard ও Howard কে বক্স A, B ও C ধরে নিলেই কাঙ্ক্ষিত সমধান পাওয়া যাবে। আবারো মনে করি যে আমরা বল 5 টি একসারিতে সাজিয়েছি।
এখন, আবারো এদের মধ্যে অবস্থিত 4 টি খালি জায়গা থেকে 2 টি বেছে নিতে পারি আমরা। তাহলেই, A, B ও C এর জন্য আমরা 5 টি বলকে তিন ভাগে বিভক্ত করে ফেলতে পারব। সুতরাং, উত্তর হবে 4C2 বা 6 ।
সমস্যা – ৪ : ধরা যাক, তুমি একটি এনালগ ঘড়ির দিকে তাকিয়ে দেখলে ঘড়ির কাঁটাটি 5 ও 6 এর মধ্যে, আর মিনিটের কাঁটাটি 6 ও 7 এর মধ্যে আছে। কিছুক্ষণ পর ফিরে এসে দেখলে এখন মিনিটের কাঁটাটি 5 ও 6 এর মধ্যে, আর ঘণ্টার কাঁটাটি 6 ও 7 এর মধ্যে আছে। তোমার কাছে মনে হল যে ঘণ্টার ও মিনিটের কাঁটাটি কেবল নিজেদের জায়গা অদলবদল করেছে! প্রশ্ন হচ্ছে, সময় দুইটি কত?
সমাধান :
(প্রথম ঘটনা) প্রথমে ধরে নাও যে ঘড়িতে চিহ্নিত 5 দাগটি থেকে ঘণ্টার কাঁটাটি x দূরত্বে আছে। ঘণ্টার কাঁটা একটি ছোট দাগ অতিক্রম করলে 12 মিনিট অতিক্রান্ত হয়। ফলে, x দূরত্বের জন্য মিনিটের হিসাব হবে 12x । আর সময় হবে 5 ঘণ্টা 12x মিনিট। আবার ধরি, মিনিটের কাঁটাটি ঘড়িতে 6 চিহ্নিত দাগটি থেকে y দূরত্বে অবস্থিত। তাহলে মিনিটের হিসাব হবে 30+y । তাহলে,
(দ্বিতীয় ঘটনা) দ্বিতীয় ক্ষেত্রে ঘণ্টার কাঁটাটি 6 দাগটি থেকে y দূরত্বে আছে। ফলে, মিনিটের হিসাব হবে 12y। আবার, এই ক্ষেত্রে মিনিটের কাঁটাটি আছে 5 দাগটি থেকে x দুরত্বে। এই কারণে, সময় হবে 6 ঘণ্টা (25+x) মিনিট। সুতরাং,
এখন, এই সমীকরণ দুটি সমাধান করতে হবে। প্রথমে, উপরের সমীকরণ দুটি যোগ করব।
এরপর, যেকোনো একটি সমীকরণ ব্যবহার করলেই একটি চলকের মান বের হয়ে যাবে। এরপর ঠিক উপরের সমীকরণ ব্যবহার করলে আরেকটি চলকের মান পাওয়া যাবে।
এবং,
অতএব, সময় দুটি হচ্ছে 5 ঘণ্টা 420/13 মিনিট এবং 6 ঘণ্টা 360/13 মিনিট।
সমস্যা – ৫ : শাকুরের 5 জন বন্ধু ঈদের দিন শাকুরের বাসায় বেড়াতে এল। এরপর কোলাকুলি শুরু হল। (কে কার সাথে কোলাকুলি করেছে বা করেনি তা আমরা জানি না!) কোলাকুলির পর্ব শেষ হওয়ার পর শাকুর লেমোনেড আনতে বাইরে গেল। ফিরে আসার পর শাকুর প্রত্যেককে আলাদাভাবে জিজ্ঞেস করল, “তুই কতজনের সাথে কোলাকুলি করেছিস?” উত্তরে প্রত্যেকেই ভিন্ন ভিন্ন সংখ্যা বলল। প্রশ্ন হচ্ছে, শাকুর নিজে কতজনের সাথে কোলাকুলি করেছে?
সমাধান : একজন সর্বোচ্চ 5 জনের সাথে আর সর্বনিম্ন 0 জনের সাথে কোলাকুলি করতে পারে। কিন্তু, কেউ একজনও যদি কোলাকুলি না করে তাহলে কিন্তু কারো পক্ষে 5 জনের সাথে কোলাকুলি করা সম্ভব না। (অর্থাৎ, 0 আর 5 পরস্পরবিরোধী) ফলে, হয় 0,1,2,3,4 অথবা 1,2,3,4,5 এই সংখ্যাগুলো শাকুরের বন্ধুরা বলেছে। কিন্তু, এই দুটি অবস্থা বিবেচনা করার আগে আমাদের অন্য একটা আইডিয়া বুঝতে হবে।
ধরা যাক, A, B ও C এই তিনজন কোলাকুলি করেছে। এক্ষেত্রে তিনটি কোলাকুলি সম্ভব; A-B, B-C, C-A । আমরা যদি প্রত্যেককে আলাদা করে জিজ্ঞেস করি কতগুলো কোলাকুলি তারা করেছে তাহলে তারা প্রত্যেকেই উত্তর দিবে 2 । এদের উত্তরে বলা সংখ্যাগুলো যোগ করলে দাঁড়ায় 6, যা মোট কোলাকুলি সংখ্যার দ্বিগুণ। (কারণ, আমরা যখন তাদের উত্তরে বলা সংখ্যাগুলো যোগ করেছি তখন আসলে, প্রত্যেকটি কোলাকুলি দুইবার গণনা করা হয়েছে!) সুতরাং, আমরা যা জানতে পারলাম তা হচ্ছে শাকুরের বন্ধুদের উত্তরে বলা সংখ্যাগুলোর সাথে শাকুর যতগুলো কোলাকুলি করেছে সেই সংখ্যা যোগ করলে যোগফল হবে জোড়। (দুই এর গুণিতক অবশ্যই জোড় হবে।)
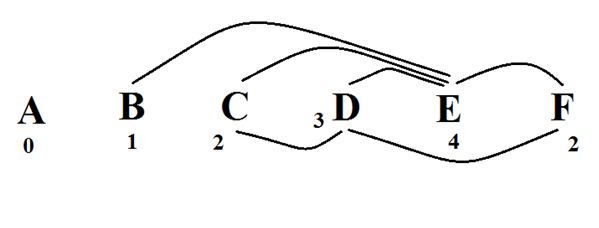
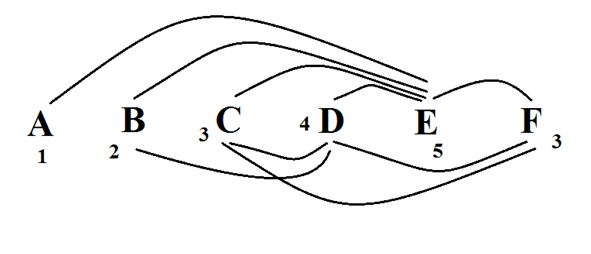
এখন 0,1,2,3,4- এই কেসটি বিবেচনা করি। এদের যোগফল হচ্ছে 10 । এখন, তাহলে শাকুরের কোলাকুলির সংখ্যা হতে পারে 0,2,4 । এক্ষেত্রে 0 উত্তর হতে পারবে না। কারণ, তাহলে যেই বন্ধু উত্তরে 4 বলেছে সে কোলাকুলির জন্য চারজনকে পাবে না। এই প্যারাডক্সের জন্য 0 বাদ পড়ে গেল। আবার 4 ও উত্তর হতে পারে না। কারণ, যেই বন্ধু উত্তরে 4 বলেছে সে যদি চারজনের সাথে কোলাকুলি করে ফেলে তাহলে শাকুর সর্বোচ্চ 3 জনের সাথে কোলাকুলি করতে পারবে। (যে শূন্য বলেছে সে প্রথমেই বাদ। আর যে এক বলেছে সে যদি আর কারো সাথে কোলাকুলি করে তাহলে তার উত্তর ঠিক থাকছে না!) বাকি থাকল 2 । নিচের চিত্র দেখলেই বুঝা যাবে যে, 2 হচ্ছে উত্তর। (শাকুরকে F দ্বারা প্রকাশ করা হয়েছে, আর তার বন্ধুদের A, B, C, D ও E দ্বারা।)
আবার, 1,2,3,4,5- এই কেসটি বিবেচনা করতে হবে। এক্ষেত্রে যোগফল দাঁড়াচ্ছে 15 । ফলে মোট যোগফল জোড় করতে শাকুরকে বিজোড় সংখ্যক কোলাকুলি করতে হবে। সম্ভাব্য উত্তর তাই 1,3,5 । প্রথমেই 1 বাদ, কারণ, যে উত্তরে 5 বলেছে সে সবার সাথে কোলাকুলি করার পর দুই জন বাদ পড়ে যাচ্ছে। (যে 1 বলেছে সে আর শাকুর নিজে ।) ফলে, যে 4 বলেছে সে তার বাকি তিনটি কোলাকুলি সম্পন্ন করার জন্য মাত্র দুইজনকে পাবে। আবার, 5 ও হতে পারে না। কারণ, যে উত্তরে 5 বলেছে সে কোলাকুলি সম্পন্ন করার পর যে উত্তরে 1 বলেছে সে বাদ পড়ে যাচ্ছে। ফলে, শাকুর নিজে সেই উত্তরে 1 বলা বন্ধুর সাথে কোলাকুলি করতে পারছে না। বাকি থাকল শুধু 3।
অবশেষে উত্তর যা পাচ্ছি তা হচ্ছে “হয় 2, অথবা 3”!

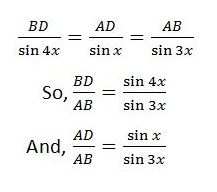
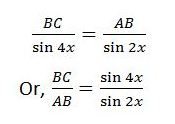
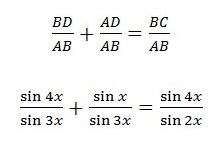
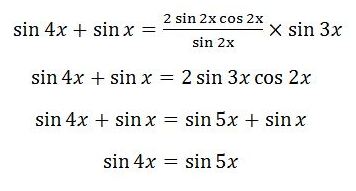
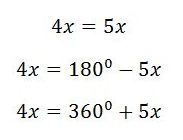
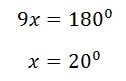
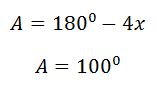
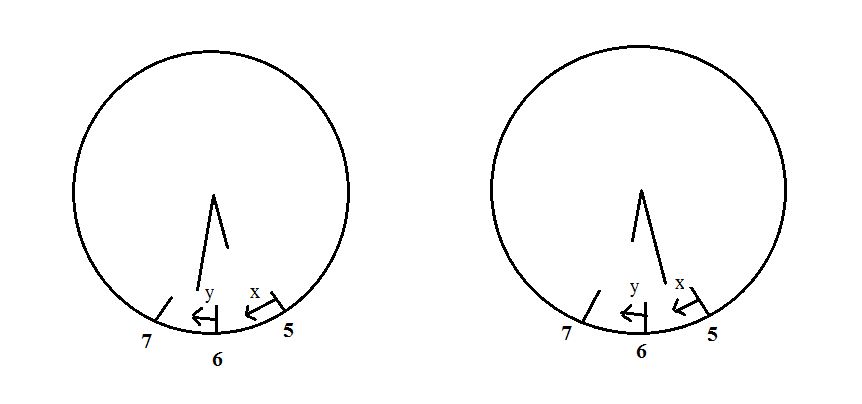
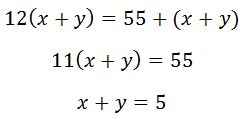
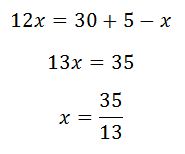
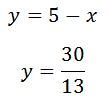

লেখাটির জন্য ধন্যবাদ…