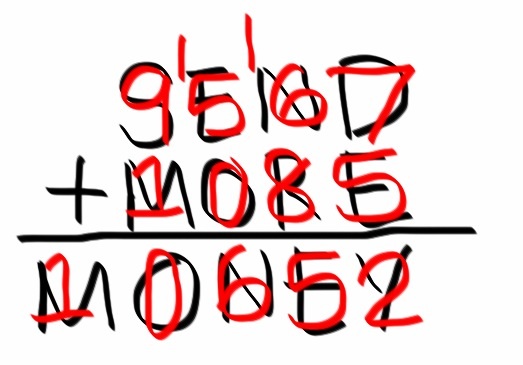ক্রিপ্টারিদমস ও আলফামেটিক্স ( অঙ্কের ধাঁধা )

ক্রিপ্টারিদমস হল অদ্ভুত ধরণের গাণিতিক ধাঁধা (puzzle) যেখানে সংখ্যার যোগ বিয়োগ গুণ ভাগ ইত্যাদি হিসেব ভিন্ন ভিন্ন অক্ষর দ্বারা নির্দেশিত থাকে। প্রতিটি অক্ষর এক একটি নির্দিষ্ট অঙ্ককে নির্দেশ করে এবং কেবলমাত্র একটি অঙ্কই নির্দেশ করে। অর্থাৎ এক একটি অঙ্ক এক একটি অক্ষরের মাঝে লুকিয়ে থাকে। ধাঁধা সমাধান করতে হয় ঐ অক্ষরগুলো থেকে গাণিতিক যুক্তির মাধ্যমে, লুকানো অংকগুলো পুনঃরুদ্ধার করে গোটা গাণিতিক হিসেব সম্পূর্ণ করার মাধ্যমে।

আলফামেটিক্স বা আলফামেট্রিক্স হল ক্রিপ্টারিদমস এরই একটা অংশ, যেখানে অক্ষরগুলো শুধু অক্ষর হিসেবেই থাকে না বরং অর্থপূর্ণ শব্দ তৈরি করে। সবচেয়ে বিখ্যাত আলফামেটিক্সটি তৈরি করেছেন পাজলিস্ট ডুডিনি (১৯২৪) :

এখানে প্রতিটি অক্ষর এক একটি নির্দিষ্ট অঙ্ককে নির্দেশ করে, তবে কোন অঙ্ক কোথায় বসবে তা বের করতে হবে গানিতক যুক্তির মাধ্যমে। কি রকম যুক্তি দরকার এখানে? না, কঠিন কিছুই দরকার নেই। শুধু গুনতে পারলেই এই ধাঁধা সমাধান করা সম্ভব। তবে অনেক ধৈর্য আর আত্মবিশ্বাস প্রয়োজন, মাথা গরম করলে চলবে না। আর একবার নিজে নিজে সমাধান করতে পারলে আনন্দের আর সীমা থাকবে না। এই ধরণের ধাঁধা সমাধানের আরেকটি উপকারিতা হল, এগুলো যত অনুশীলন করবে ততই চিন্তাশক্তি বাড়বে।

তাহলে চল দেখা যাক, কী করে সমাধান করতে হয়  আলফামেটিক্স। একটা করলেই আয়ত্বে চলে আসবে; আর শেষে থাকছে নিজে করার জন্য বেশ কিছু অদ্ভুত, সুন্দর আর মজার আলফামেটিক্স।

আমরা নিচের এই বিখ্যাত আলফামেটিক্স দিয়েই শুরু করি, এর বিশেষত্ব হচ্ছে এর একটি মাত্রই সমাধান আছে।

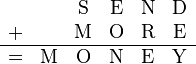       [শর্ত: একটি অক্ষরের জন্য একটি ও কেবল একটি অঙ্কই প্রযোজ্য; ০-৯ পর্যন্ত যে কোন অঙ্ক ব্যবহার করা যাবে; আর সর্ব প্রথম অঙ্ক 0 হবে না]

দেখা যাক এ সমস্যাকে কীভাবে আক্রমণ করে বের করে নিয়ে আসা যায় ভেতরের গুপ্ত সংখ্যা, তবে একটি জানা বিষয় মাথায় রাখতে হবে যে, ২ টি অঙ্ক যোগ করার সময় কখনই হাতে 1 এর বেশি অবশিষ্ট থাকতে পারে না। কেননা, ২ টি ভিন্ন অঙ্কের (8,9) সর্বোচ্চ সমষ্টি 17 হতে পারে এবং সেক্ষেত্রেও হাতে 1 বাকি থাকে।

[বিঃদ্রঃ সমাধান করার সময়ে হাতে অবশিষ্ট কিছু যোগ করার জন্য [ ] ব্র্যাকেট ব্যবহার করেছি। এছাড়া সম্ভাব্য মান লিখার সময়েও [ ]  ব্যবহার করেছি। এবং ব্যাখ্যা দেয়ার জন্য ( ) ব্রাকেট ব্যবহার করেছি। আমরা কাজ শুরু করেছি বাম থেকে ডানে  (যোগ করার আসল নিয়মের বিপরীত)। এবং O এবং 0 (zero) কে আলাদাভাবে বোঝার সুবিধার্থে O লিখা হয়েছে ‘O’ এভাবে। আর সুবিধের জন্য একটু পর পর সমস্যার চিত্র দেওয়া হয়েছে]

সমাধানঃ

• আমরা প্রথমেই বলতে পারি এখানে M এর মান অবশ্যই 1 হবে; কারণ, S ও M যোগ করে আমরা M পাব। আমাদের স্বীকার্য অনুযায়ী এ যোগফল সর্বোচ্চ 17 হতে পারে। এবং যদি আগের হাতে থাকা অঙ্ক থাকেও, তাহলে মোট সমষ্টি 18 হবে; অর্থাৎ M=1 ই হবে  (আরও একটি যুক্তি: ২টি ৪ অঙ্কের সংখ্যার যোগফল কোনক্রমেই 19999 এর বেশি হতে পারে না)।

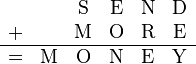
• এবার সহস্রের ঘরের যোগ, S+M+[0/1]=10+‘O’ (কারণ, S,M ও [0/1] এর যোগফল অবশ্যই 10 এর বেশী হবে, না হলে যোগফল 5 অঙ্ক বিশিষ্ট হতে পারে না এবং যোগফলের একক স্থানীয় অঙ্ক ‘O’ নির্দেশ করে); যেহেতু M=1, তাই S+1+[0/1] =10 + ‘O’। এখন সমষ্টির এর মান 10 এর বেশী হতে হলে S=8 (যখন হাতে 1 থাকে) অথবা S=9 (যখন হাতে ০ থাকে) হতে হবে। তাহলে, S=[8/9] যাই হোক না কেন ‘=’ এর ডান পাশে সমষ্টি 10 হবে। অর্থাৎ, 10+‘O’=10। অতএব ‘O’=0।

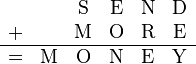
• এবার শতকের ঘরের যোগ, E+‘O’+[0/1]=N। যেহেতু ‘O’=0 তাই, E+0+[0/1]=N। এখানে স্পষ্টত হাতে অবশিষ্ট অঙ্ক 0 হতে পারে না ( কারণ, সেক্ষেত্রে E=N হয়ে যায়)। তাহলে, E+[1]=N। এখন শতকের ঘরের যোগের ক্ষেত্রে, E+[1]=N , এই অংশ হিসেব করার পর হাতে কিছুই থাকে না (কারণ হাতে 1 অবশিষ্ট থাকার জন্য E=9 হতে হবে, কিন্তু সেক্ষেত্রে N=0(10 এর 0) হতে হবে; যা সম্ভব নয় যেহেতু ইতোমধ্যে ‘O’=0)। যেহেতু হাতে কিছু নেই, তাই সহস্রের কলামে, S=9 হবে (২ নং পয়েন্টের বোল্ড হরফ দেখুন)

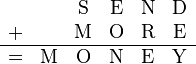
• এবার দশকের ঘরের যোগ, N+R+[0/1]=10+E (আমরা ধরে নিচ্ছি N,R এবং [0/1] এর যোগফল 10 এর চেয়ে বড়, সামনে যদি আমাদের ধরে নেওয়ার জন্য ভুল হয় বা ধরা খাই তবে আমরা আবার এখানে এসে অন্য কিছু ধরব 😛 ); অথবা,(E+1)+R+[0/1]=10+E (যেহেতু, E+1=N); অথবা, R+[0/1]=9; অতএব R=[8/9], কিন্তু S=9; তাই, R=8।

• এবার এককের ঘরের যোগ, D+E=10+Y (আমরা ধরে নিচ্ছি D এবং E এর যোগফল 10 এর চেয়ে বড়, সামনে যদি আমাদের ধরে নেওয়ার জন্য ভুল হয় বা ধরা খাই তবে আমরা আবার এখানে এসে অন্য কিছু ধরব 😛 ) । E+1=N অর্থাৎ, E=N-1, এই মান সমীকরণে বসিয়ে, D+N=10+1+Y। এখন, S=9,R=8। তাই D ও N এর সর্বোচ্চ যোগফল সম্ভব D+N=6+7=13=Y+11। অর্থাৎ, Y<=2; কিন্তু ‘O’=0,M=1; তাই, Y=2 । একই সাথে এটাও সত্য, D+N=6+7 ।

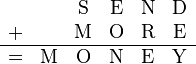
• আমাদের সর্বশেষ ২টি শর্ত, E+1=N ,

D+N=6+7

এখন যদি N=7 হয় তবে, D=6; এবং E+1=7; বা, E=6। কিন্তু D ও E উভয়ই 6 হওয়া সম্ভব নয়। তার মানে, N=6,D=7 এবং সর্বশেষ E=5।

তাহলে সম্পূর্ণ সমাধানঃ

এটার মত করেই যেকোন ধরণের আলফামেটিক্স সমাধান করা যাবে। যোগ-বিয়োগ-গুণ-ভাগ যাই থাকুক না কেন, শুধু যুক্তি অনুযায়ী সামনে আগাতে থাকব, দরকার পড়লে কিছু ধরে নিব; ধরে ধরা খেলে আবার পিছনে ব্যাক করে নতুন কিছু ধরব  😛

এবার নিজে করার জন্য কিছু আলফামেটিক্সঃ [এগুলো প্রোগ্রামিং করে করারও চেষ্টা করতে পার]

1. WRONG+WRONG=RIGHT
2. RAIN+RAIN+GO=AWAY
3. আমার+সোনার=বাংলা
4. DRUNK+DRIVE=KILLED
5. ODD+ODD=EVEN
6. ALPH+.A.+METICS [. ও অক্ষর ধরে নিতে হবে]
7. EARTH+AIR+WATER+FIRE=NATURE
8. FOUR+ONE+THREE+THREE=ELEVEN
9. FORTY+TEN+TEN=SIXTY
10. SANTA-CLAUS=XMAS
11. BANK+CASH=CHECK
12. TWO=√SQUARE
13. HAVE+SOME+SUMS+TO=SOLVE
14. 1971+FIGHTERS-RAJAKAR=BANGLADESH
15. SHOSHIKKHA+.+COM=SHOPNO
16. GOOD-BYE= 😀
17. SEE+U+AGAIN= 😈    😆  😀  😉