নামটা ইচ্ছা করেই এমন দেয়া। আজ এমন একটা সমস্যা ( আচ্ছা,সমস্যা তো একটা না,দুইটা ) নিয়ে আলোচনা করবো,যেটার নাম শোনার পর যে কারো মনে হবে যে এটা অদ্ভূত রকম সহজ একটা সমস্যা,তবে প্রথমবার সমাধান করতে গেলে কিছুটা বিপাকে পড়ে যেতে হয় মাঝেমধ্যে। সমস্যাটা তাহলে বলিঃ
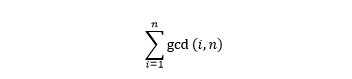
আরেকটা হচ্ছেঃ
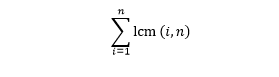
প্রথম সমস্যাটাকে যদি সহজ ভাষায় বলি,
“1 থেকে n পর্যন্ত সবগুলো সংখ্যার সাথে n এর গ.সা.গু. বের করে তাদের যোগফল বের কর”
আর দ্বিতীয় সমস্যাটা হুবুহু একই,শুধু গ.সা.গু. এর জায়গায় ল.সা.গু. বসিয়ে দিতে হবে,এই আর কি।
“1 থেকে n পর্যন্ত সবগুলো সংখ্যার সাথে n এর ল.সা.গু. বের করে তাদের যোগফল বের কর”
উদাহরণ দিয়ে যদি বুঝাই তাহলে,
” n = 6 হলে, gcd(1,6) + gcd(2,6) + gcd(3,6) + gcd(4,6) + gcd(5,6) + gcd(6,6) = 1+2+3+2+1+6 = 15 “
আর দ্বিতীয় সমস্যাটার ক্ষেত্রে উপরের উদাহরণটা চেঞ্জ হয়ে যা হবে,
” n = 6 হলে, lcm(1,6) + lcm(2,6) + lcm(3,6) + lcm(4,6) + lcm(5,6) + lcm(6,6) = 6+6+6+12+30+6 = 66 “
সমাধানঃ
অবশ্যই এবং অবশ্যই হাতে হাতে কলমে কলমে ১ থেকে n পর্যন্ত সবার জন্যে গসাগু/লসাগু বের করে যোগ যে করবো না,সেটা তো নিশ্চিত সবাই। যদি তাই করতে হতো,আজকে এই পোস্ট লিখার কোনো দরকারই ছিলো না। n = 1000000000 দিয়ে দিলে,হাতে কলমে কেন,শক্তিশালী কম্পিউটার দিয়েও ১০ সেকেন্ডের মত সময় লেগে যাবে!
তাহলে কি করা যায়?
আমরা যখন ১ থেকে n পর্যন্ত স্বাভাবিক সংখ্যাগুলোর সাথে n এর গসাগু বের করার চেষ্টা করছি,তখন আসলে আমরা কি প্রতিবার n এর সবগুলো বিভাজক নিয়ে ( একেকটা বিভাজক বিভিন্ন সংখ্যকবার নিয়ে ) তাদের যোগফলটাকেই উত্তর হিসেবে দিচ্ছি না?
উপরের উদাহরণটাই দেখা যাকঃ n = 6 এর জন্যে 1+2+3+2+1+6 এদের যোগফলটাই আমাদের উত্তর। এখানে 1,2,3,6 ছাড়া অন্য কোনো সংখ্যা নেই। একেকটা বিভাজক হয়তো বিভিন্ন সংখ্যকবার আছে। তো সমস্যা সমাধানের খাতিরে ধরেই নিই আপাতত যে,কোন বিভাজক কতবার করে আসবে সেটা আমরা কোনো একটা যাদুর সাহায্যে বের করে ফেলতে পারবো।
তাহলে আমাদের সমস্যাটা গিয়ে দাঁড়াচ্ছে যে, n এর যে কয়টা বিভাজক আছে,তাদেরকে খুঁজে বের করা। এই কাজটা খুব দ্রুত বের করে ফেলা যায়! যারা প্রোগ্রামিং করো,তারা হয়তো জানোই,একটা সংখ্যার বিভাজকগুলো বের করতে ![]() পরিমাণ সময় দরকার। আর যারা প্রোগ্রামিং এর সাথে যুক্ত নেই,তাদের বুঝার জন্যে বলছি, এক এক করে সবার গ সা গু বের করে যোগ করতে যদি আমাদের ১০০০০ ঘণ্টা লাগতো,এখন আমাদের সময় লাগবে মাত্র ১০০ ঘণ্টা!
পরিমাণ সময় দরকার। আর যারা প্রোগ্রামিং এর সাথে যুক্ত নেই,তাদের বুঝার জন্যে বলছি, এক এক করে সবার গ সা গু বের করে যোগ করতে যদি আমাদের ১০০০০ ঘণ্টা লাগতো,এখন আমাদের সময় লাগবে মাত্র ১০০ ঘণ্টা!
তাহলে n = 6 এর জন্যে আমাদের সমাধানটা গিয়ে দাঁড়ালো অনেকটা এমনঃ
![]() c1 , c2 , c3 , c4 এগুলো হচ্ছে সেই ম্যাজিক ভ্যালু,যেগুলো আমরা এখনো জানিনা। এবার একটু মনোযোগ দিতে হবেঃ
c1 , c2 , c3 , c4 এগুলো হচ্ছে সেই ম্যাজিক ভ্যালু,যেগুলো আমরা এখনো জানিনা। এবার একটু মনোযোগ দিতে হবেঃ
১ থেকে n পর্যন্ত স্বাভাবিক সংখ্যাগুলোর সাথে n এর গসাগু বের করতে গেলে,গসাগু এর মান ১ কতবার আসবে,সেই সংখ্যাটা প্রকৃতপক্ষে n এর অয়লার ফাংশন এর মান। যারা এ ব্যাপারে জানো না,তারা এই লিংক থেকে পড়াশোনা করে আসতে পারো।
সহজ ভাষায় বলতে গেলে phi(n).
phi(6) = 2
এখন কোন কোন জোড়ার গসাগু করলে আমরা মান ১ পাই? এরা হচ্ছে (১,৬) এবং (৫,৬) . তাহলে প্রথম ম্যাজিকাল ভ্যালু c1 = 2. আমরা c1 এর মান খুব সহজেই বের করে ফেললাম।
এবার c2 এর পালা। ১ থেকে n পর্যন্ত স্বাভাবিক সংখ্যাগুলোর সাথে n এর গসাগু বের করতে গেলে,গসাগু এর মান ২ কতবার আসবে,সেই সংখ্যাটা বের করার জন্যে আমাদের প্রথমে বের করতে হবে phi(6/2) = phi(3) এর মান। যেহেতু 3 একটি মৌলিক সংখ্যা , তাই phi(3) = 2. [ কেননা,phi(p) = p-1 ]
phi(3) = 2 . এর মানে হচ্ছে ১ থেকে ৩ পর্যন্ত এমন দু’টি সংখ্যা আছে,যাদের সাথে ৩ এর গ সা গু হবে ১. জোড়াগুলো হচ্ছে (১,৩) এবং (২,৩)
এবার একটা মজার কাজ করবো। এইযে দু’টো জোড়া পেলাম,এই জোড়ার প্রত্যেককে আমি ২ দিয়ে গুণ করে দিবো! কেন ২ দিয়ে? কারণ আমার মূল সংখ্যাটা ছিলো n = 6. আমি phi() এর মান বের করার সময় ৬ কে ২ দিয়ে ভাগ করে নিয়েছিলাম।
২ দিয়ে গুণ করে যা পাই, (১২,৩২) এবং (২২,৩২) = (২,৬) এবং (৪,৬)! এদের গ সা গু ই তো ২! তার মানে আমরা c2 = 2 এর মান ও বের করে ফেললাম!
একইভাবে c3 এর মান বের করে ফেলি। এটা আর কিছুই না,phi(6/3) = phi(2) = 1
বুঝতেই পারছো,c4 হবে phi(6/6) = phi(1) = 1
তার মানে,সব কিছু মিলিয়ে বলতে গেলে বলা যায়ঃ
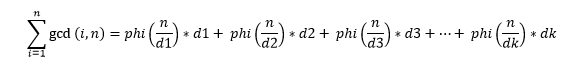
যেখানে আমরা ধরে নিয়েছি যে ,n এর মোট বিভাজক সংখ্যা হচ্ছে k এবং ![]() এরা হচ্ছে n এর বিভাজক সমূহ।
এরা হচ্ছে n এর বিভাজক সমূহ।
উদাহরণঃ
১) n = 14 হলে,
gcd(1,14) + gcd(2,14) + gcd(3,14) + gcd(4,14) + gcd(5,14) + gcd(6,14) + gcd(7,14) + gcd(8,14) + gcd(9,14) + gcd(10,14) + gcd(11,14) + gcd(12,14) + gcd(13,14) + gcd(14,14)
= 1 + 2 + 1 + 2 + 1 + 2 + 7 + 2 + 1 + 2 + 1 + 2 + 1 + 14
= 39
এটা তো গেল সাধারণভাবে সমাধান প্রক্রিয়া। এবার আমাদের উপর্যুক্ত আলোচনার প্রেক্ষিতে যদি হিসেব করতামঃ
n = 14 এর জন্যে বিভাজকসমূহ হচ্ছে ঃ 1 , 2 , 7 , 14
phi(14/14) = phi(1) = 1 [ (1,1) এর গ সা গু 1 ]
phi(14/7) = phi(2) = 1 [ (1,2) এর গ সা গু 1 ]
phi(14/2) = phi(7) = 6 [ (1,7) , (2,7) , (3,7) , (4,7) , (5,7) , (6,7) এদের সবার গ সা গু ই 1 ]
phi(14/1) = phi(14) = 6 [ (1,14) , (3,14) , (5,14) , (9,14) , (11,14) , (13,14) এদের সবার গ সা গু ই 1 ]
তাহলে,আমাদের নির্ণেয় যোগফল হবেঃ
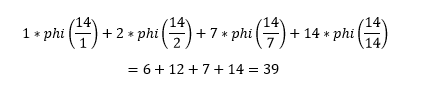
তাহলে,আমাদের আজকের আলোচনার প্রথম সমস্যাটি সমাধান করা হয়ে গেলো। এই সমস্যাটার সমাধান বুঝে গেলে পরের সমস্যাটার সমাধানে তেমন একটা বেগ পেতে হবে না।
এই সমস্যাটিতে আমাদের বের করতে হবে ১ থেকে n পর্যন্ত সবগুলো সংখ্যার সাথে n এর ল.সা.গু. বের করে তাদের যোগফল। এর সমাধানে মুখের কথার চেয়ে খাতা কলমে একটু গণিত করে যেতে হবে।
১ থেকে n পর্যন্ত সবগুলো সংখ্যার সাথে n এর ল.সা.গু. বের করে তাদের যোগফল কে আমরা সুবিধার খাতিরে ধরে নিই LCMSUM. তাহলে বলা যায়ঃ
![]()
আমরা জানি, lcm(n,n) = n. এবার,
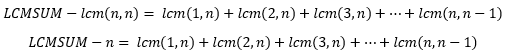
এবার উপরের দুই লাইন সমীকরণের প্রথমটিকে ১নং সমীকরণ ধরে (১) + (১) করে ফেলিঃ
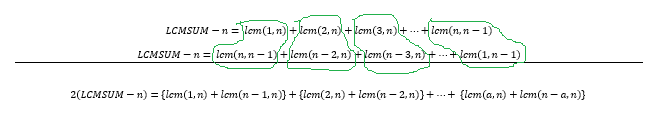
১নং সমীকরণ কে নিজের সাথেই যোগ দিয়েছি উপরের ছবিটায়। শুধু দ্বিতীয় লাইনে যোগের বেলায় আমরা সমীকরণটাকে উলটা করে লিখেছি। যেখানে lcm(n,n-1) একদম শেষে ছিলো,তাকে শুরুতে নিয়ে এসেছি। এমনটা করাই যায়। এতে যোগফলে কোনোই পরিবর্তন হয় না। কেননা, a + b যেই কথা , b + a একই কথা।
যোগফলটাকে আমরা কিঞ্চিং পরিবর্তন করে এভাবে লিখতে পারিঃ
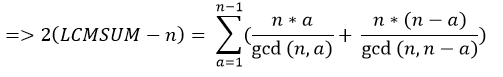
এবার এই যোগফলটা থেকে কিছু গুরুত্বপূর্ণ সমীকরণ বের করতে হবে। তার আগে আমাদের জেনে রাখা দরকারঃ
১) gcd(n,a) = gcd(n,n-a)
প্রমাণঃ ধরে নিই, একটি পূর্ণ সংখ্যা d = gcd(n,a) . তাহলে n এবং a সংখ্যা দুইটি অবশ্যই d দিয়ে বিভাজ্য এবং d হচ্ছে n এবং a এর সবচেয়ে বড় সাধারণ বিভাজক! ( গ সা গু এর মানেই তো সেটা )
এবার অনুমান করে নিই, d = gcd(n,n-a) . আমাদের অনুমান সঠিক প্রমাণ করতে পারলেই কাজ শেষ। খেয়াল করে দেখি, n এবং n-a এর সবচেয়ে বড় বিভাজক যদি d হয়,তাহলেই অনুমানটি সঠিক হয়ে যাবে! আমরা তো উপরের লাইনে বলেই দিয়েছি যে n এর সবচেয়ে বড় সাধারণ বিভাজক হচ্ছে d ( a এর সাথে গ সা গু বের করার বেলায় )। কিন্তু মজার ব্যাপার কি , n-a এর ক্ষেত্রেও এই বিভাজকটা d নিজেই,কেন না আমরা এভাবে লিখতে পারি চাইলেঃ
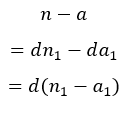
n এর ক্ষেত্রে d সবচেয়ে বড় সাধারণ বিভাজক,যা a এর ক্ষেত্রেও সত্য।
তার মানে, n-a ও a এর ক্ষেত্রেও সবচেয়ে বড় সাধারণ বিভাজক হচ্ছে d. তাহলে বলা যায়,আমাদের অনুমান সঠিক!। 😀
এবার ছোট্ট একটু অংক করে এসে আমাদের সমস্যাটিকে আরেকটু ছোট করে নিয়ে আসা যায়ঃ
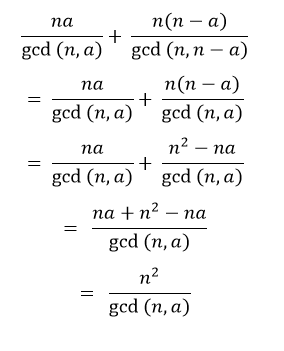
অনেকটুক এগিয়ে গেলাম,আমাদের মূল সমীকরণটিকে তাহলে এবার এমন দেখাবেঃ
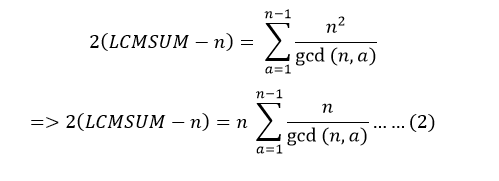
এবার আমি একটা claim করবো। প্রমাণ না করতে পারলে কিছুটা কষ্ট পাবো,তবে অয়লার ফাংশনের ব্যাপারে ধারণা থাকলে প্রমাণ করতে বেগ পেতে হবে না। Intuitive proof হলেও হবে। আমার claim টা হচ্ছেঃ
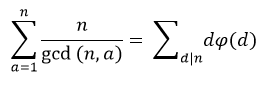
উপরের ঐ চিহ্নটার নামই হচ্ছে ফাই (phi)
এর মানে হচ্ছে , n এর যত বিভাজক আছে , সবার অয়লার ফাংশনের মানের সাথে বিভাজকগুলোকে গুণ করে যোগ করে দিলে আমরা উপরোক্ত মানটি পেয়ে যাবো। Intuition থেকে ধরতে যদি না পারো,জানিয়ে দিও কমেন্ট বক্সে।
তাহলে এবার ২ নং সমীকরণকে আরো ছোট করে নিয়ে আসা যায় এভাবেঃ

একবারে না বুঝলে,দুইবার পড়ো। তিনবার পড়ো। খাতা কলম খুলে নিজেরা লিখে লিখে দেখো। বুঝা যাবে আশা করি। এখন n = 100000000000000 = 1e14 দিলেও আমরা ১ সেকেন্ডের ও কম সময়ে সমাধান বের করে ফেলতে পারবো।
উদাহরণঃ
১) n = 14 হলে,
lcm(1,14) + lcm(2,14) + lcm(3,14) + lcm(4,14) + lcm(5,14) + lcm(6,14) + lcm(7,14) + lcm(8,14) + lcm(9,14) + lcm(10,14) + lcm(11,14) + lcm(12,14) + lcm(13,14) + lcm(14,14)
= 14 + 14 + 42 + 28 + 70 + 42 + 14 + 56 + 126 + 70 + 154 + 84 + 182 + 14
= 910
আর এই প্রক্রিয়ায়ঃ
n = 14 এর জন্যে বিভাজকসমূহ হচ্ছে ঃ 1 , 2 , 7 , 14
phi(1) = 1 [ (1,1) এর গ সা গু 1 ]
phi(2) = 1 [ (1,2) এর গ সা গু 1 ]
phi(7) = 6 [ (1,7) , (2,7) , (3,7) , (4,7) , (5,7) , (6,7) এদের সবার গ সা গু ই 1 ]
phi(14) = 6 [ (1,14) , (3,14) , (5,14) , (9,14) , (11,14) , (13,14) এদের সবার গ সা গু ই 1 ]
অতএব,
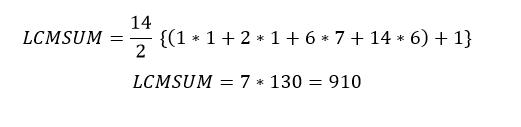
ধন্যবাদ সবাইকে ধৈর্য নিয়ে পড়ার জন্য! স্বশিক্ষার সাথেই থাকো!


১নং সমীকরণ ধরে (১) + (১) in here
lcm(1,n-1) it will be lcm(1,n) won’t it?
because lcm ( n – (n-1) ,1) = lcm (1 , n) ;
then it will be true { lcm (a,n) + lcm (n-a , n) };
where a=n-1;
১নং সমীকরণ ধরে (১) + (১) in here
lcm(1,n-1) it will be lcm(1,n) won’t it?
because lcm ( n – (n-1) ,n) = lcm (1 , n) ;
then it will be true { lcm (a,n) + lcm (n-a , n) };
where a=n-1;