নামটা শুনেই পিছিয়ে পড়ো না প্লিজ। বিশ্বাস করো , ব্যাপারটা সুন্দর। এডমিশনে আসা কঠিন ইন্টিগ্রেশনগুলোর একটা vital part হচ্ছে এই স্টেপটুকু। যদি আয়ত্তে নিয়ে আসতে পারো,লাভ ভিন্ন ক্ষতি হওয়ার কোনো কারণই দেখিনা। তো কথা না বাড়িয়ে কাজে চলে যাই!
আচ্ছা , তোমরা যখন দু’টো ভগ্নাংশকে যোগ করতে যাও,তখন কীভাবে করো? ভগ্নাংশগুলোর হরগুলোর ল.সা.গু নাও। তারপর যেটা করো,সেই ল.সা.গু কে ভগ্নাংশ দু’টোর হর দিয়ে ভাগ করে,ভাগফলটাকে লবগুলোর সাথে গুণ দিয়ে যোগ দিয়ে বসিয়ে দাও! মাথা ঘুরে গেল? দেখে আসি একটা উদাহরণঃ
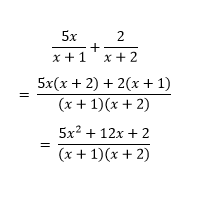
দু’টো ভগ্নাংশকে যোগ করা হলো এখানে। এখন বিপত্তিটা বাঁধে কখন জানো? যখন আমরা এই যোগফল থেকে ভগ্নাংশ দু’টোকে আলাদা করতে যাবো। উপরের এই উদাহরণ থেকে আলাদাকরণ প্রক্রিয়াটা হয়তো অনেক সহজ! কারণ লব এর অংশটুকুকে উৎপাদকে ভেঙে ফেললেই কাজ একদম সহজ হয়ে যায়। কিন্তু কিছু কিছু যোগফল থেকে ভগ্নাংশগুলোকে টেনে হিচড়ে বের করাটা বেশ দুঃসাধ্য!
যেমনঃ
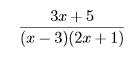
এই ভগ্নাংশটাকে উপরের নিয়মে Split করতে গেলেই বিপাকে পড়ে যাবে। Split এমনভাবেই করতে হবে,যেন প্রতিটা ভগ্নাংশের হরের অংশে (x-3) এবং (2x+1) এর উভয়েই না থাকে!
আলোচনার শুরুতে দু ধরণের ভগ্নাংশের ব্যাপারে একটু বলে নিই।
১) Proper Fraction
২) Improper Fraction
Proper Fraction হচ্ছে সেসব ভগ্নাংশ , যাদের লবের চাইতে হরে বিদ্যমান বহুপদীর মাত্রা বড়। যেমনঃ
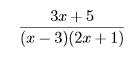
আর Improper Fraction হচ্ছে সেসব ভগ্নাংশ , যাদের লবের চাইতে হরে বিদ্যমান বহুপদীর মাত্রা ছোট বা সমান। যেমনঃ
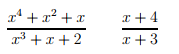
আজকের পর্বে আমরা দেখবো,একটি ভগ্নাংশ যদি Proper হয়,তাহলে তাকে কীভাবে কিছু ভগ্নাংশের সমষ্টি হিসেবে আলাদা করতে হয়।
Proper Fraction কে আলাদা করতে গেলে কয়েকটা বিষয় মাথায় রাখতে হয়। যেমনঃ
১) যখন হরে একই উৎপাদক একবারের চেয়ে বেশি থাকেনা।
২) যখন হরে একই উৎপাদক একবারের চেয়ে বেশি থাকে।
৩) যখন হরে উৎপাদকগুলোর মাঝে কেউ এমন থাকে,যে কিনা নিজেই বহুপদী!
১) যখন হরে একই উৎপাদক একবারের বেশি থাকেনা:
আমাদের উদাহরণের ভগ্নাংশটিকেই আবার টেনে নিয়ে আসি। ভগ্নাংশটার হরটার দু’টো কিউট কিউট উৎপাদক ছিলো,মনে আছে? যেহেতু এর উৎপাদক সংখ্যা দুই(২) , তাই একে আমরা দু’টো ভগ্নাংশের যোগফল হিসেবে ঠিক এভাবে উপস্থাপন করতে পারিঃ
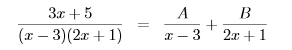——-(১)
খেয়াল রাখতে হবে,এখানে A আর B এর মান হবে ধ্রুবক কিছু। এর মাঝে চলককে নিয়ে আসা যাবেনা। যদি চলে আসে,তাহলে ওই ভগ্নাংশটুকুকে আবার Split করতে হবে।
শুরুতেই যেটা করবো , (১) এর বাম পক্ষের হর দিয়ে,পুরো ভগ্নাংশকে গুণ দিয়ে দিবো! এইযে নিচের মতো করেঃ
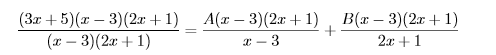
একটু কাটাকাটি করে আরেকটু ছোট করে ফেলার পর চেহারা যা দাঁড়ায়ঃ
——(2)
একটু যদি যোগ বিয়োগ গুণ করে ফেলি,তাহলে নিচের চেহারার দিকে এগোতে থাকবো!
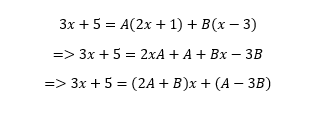
উপরের সমীকরণের উভয়পক্ষ সত্য হওয়ার জন্যে 2A+B = 3 এবং A-3B = 5 হওয়া বাধ্যতামূলক! এই দু’টো সমীকরণ থেকে A এবং B এর মান বের করে নিলে যা দাড়ায়ঃ
A = 2 এবং B = -1
A এবং B এর মান দু’টো (১) এ বসিয়ে পাইঃ
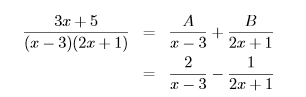
হয়ে গেলো আংশিক ভগ্নাংশে প্রকাশ! খেয়াল করে দেখেছো,পুরো প্রক্রিয়াতে আমি একবারো ” আংশিক ভগ্নাংশ ” নামটি নিই নাই। কারণ অনেকে এই নামটা শুনলেই সুন্দর মতো স্ক্রল করে চলে যেতে। এতোই অপছন্দ অনেকের কাছে এই টপিক! :p
A এবং B এর মান অন্যভাবেও বের করা যেত। আমরা চাইলে (2) এ x=3 এবং x=(-1/2) বসিয়ে A এবং B এর মান বের করে নিতে পারতাম। একই কথা।
অনুশীলনের জন্যেঃ
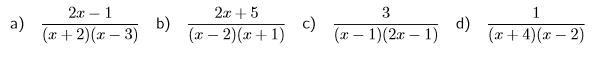
২) যখন হরে একই উৎপাদক একবারের চেয়ে বেশি থাকে:
এবার ধরো একটা ভগ্নাংশ এমন,যার হরে একই উৎপাদক একের অধিকবার আছে। যেমনঃ
তখন যেভাবে যা ধরতে এবং করতে হবে তা হচ্ছেঃ
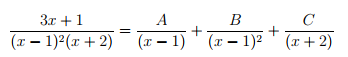————–(1)
(x-1) যেহেতু দু’বার আছে,তাই একবার,দু’বার এভাবে মোট দুইটা আলাদা ভগ্নাংশে আমাদের ভাগ করে নিতে হবে। যদি তিনবার থাকতো,একইভাবে আমাদের একবার,দু’বার,তিনবার এভাবে ভাগ করে নিলেই হয়ে যেত।
আগের মতোই এবার (১) এর উভয়পক্ষকে (x-1)^2 (x+2) দিয়ে গুণ দিয়ে দিই!
———-(2)
সমীকরণ (২) এ x=1,-2 বসিয়ে কিছু মান বের করে ফেলা যাক!
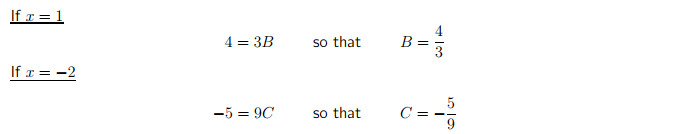
বিপত্তি বেঁধে গেল মনে হচ্ছে? A এর মান কীভাবে বের করবে? উত্তরটা হচ্ছেঃ সহগ সমীকৃত করে!
(২) নং থেকে সহগ সমীকৃত করে পাইঃ
উপরের সমীকরণে ভালো করে তাকাও! দরকার শুধু A এর মান। তো x^2 এর সহগ হচ্ছে (A+C) , কিন্তু সমীকরণের বাম দিকে x^2 পদটাই অনুপস্থিত! তার মানে , এর সহগ হচ্ছে শূণ্য!
ধরাই যায়ঃ
A+C = 0
A = -C = 5/9
হয়ে গেল! A,B,C তিনজনের মানই জানা হয়ে গেল।
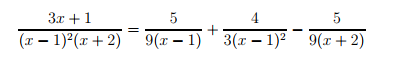
অনুশীলনের জন্যঃ
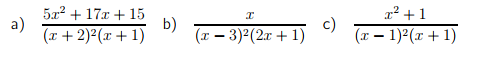
৩) যখন হরে উৎপাদকগুলোর মাঝে কেউ এমন থাকে,যে কিনা নিজেই বহুপদী:
এখন একটা ভগ্নাংশ হতে পারে এমনঃ
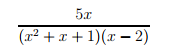
এর ক্ষেত্রে সমীকরণের ফরমেশন টা একটু আলাদা হবে,বাকি ক্যালকুলেশন সব আগের মতইঃ
——(1)
এইযে Ax+B হলো,এইটা সেই পার্টটুকুতেই হবে যার হর-এ তুমি বহুপদীটাকে বসাচ্ছো,BE CAREFUL!
এই সমস্যাটা নিজেরাই সমাধান করো! যদি দেখো A,B,C এর মান যথাক্রমে (-10/7) , (5/7) , (10/7) হয়েছে,তাহলে তোমার সমাধান সঠিক! মান বসিয়ে পেয়ে যাবে আংশিক ভগ্নাংশগুলো।
অনুশীলনের জন্যেঃ
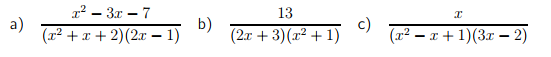
অনুশীলনের সমস্যাগুলো সমাধান করে ফেলো। আগামী পর্বে Improper Fraction কে Decompose করা শিখে নিবো,সাথে জানিয়ে দিবো অনুশীলনের উত্তরগুলো! সেই পর্যন্ত সবাই ভালো থেকো!
কৃতজ্ঞতা স্বীকারঃ
1) mathcentre for providing such wonderful and vivid examples.
Sadman Sakib
Latest posts by Sadman Sakib (see all)
- Randomized Algorithm – Competitive Programming – Part 2 - February 10, 2020
- Randomized Algorithm – Competitive Programming – Part 1 - December 24, 2019
- গ.সা.গু. এবং ল.সা.গু. – Mind Blown - December 28, 2017
স্বল্প সময়ে যেকোনোটার অংশ বের করার নিয়মটা বললে ভালো হয়।
Tnx
ভাল
Wow…… Thanks a million 🙂
khubbb valo hoyeche… awesome
kintu ekta qsn… jodi hor (x^2)/(x-1) hoy tokhn kivabe dhorbo????
ধন্যবাদ
পরের পর্বটা পাবো কিভা??
Please type a full example we can’t understand your problem
(x^2-1+1)÷(x-1)
=(x^2-1)÷(x-1)+{1÷(x-1)}
=(x^2-1^2)÷(x-1)+{1÷(x-1)}
={(x+1)(x-1)÷(x-1)}+{1÷(x-1)}
=(x+1)+{1÷(x-1)} (Ans.)
khub valo
vai … ssc higher math er (8.1-8.3) ektu bole dile valo hoyton..plz vai bolen
অনেক বেশি সহজ ও ভালো লাগছে।ধন্যবাদ সহজশিক্ষা প্রতিষ্ঠানকে।
সহগ সমীকৃত করণটা বুঝতে পারছিলাম না। এখন সলভড। ধন্যবাদ অনেক?
j tar deklam setai bujlam na??
অনেক ভালো। আমার সহগ সমীকৃত করতে একটু সমস্যা হতো।কিন্তু এখন ইনশাআল্লাহ আমি করতে পারবো।
অনেক সহজ হয়ে গেছে এখন।
ধন্যবাদ
কিন্তু পরের পর্বটা পাবো কিভা???
পরের পর্বটা পাবো কিভা??
আচ্ছা সহগ সমীকৃত সংজ্ঞা কী?
দয়া করে বলেন সহগ সমীকৃত কী?
Like!! I blog frequently and I really thank you for your content. The article has truly peaked my interest.
I like the valuable information you provide in your articles.
I like the valuable information you provide in your articles.
Hi there, after reading this amazing paragraph i am as well delighted to share my knowledge here with friends.
Thanks so much for the blog post.
shingles treatment medication dose https://www.herpessymptomsinmen.org/productacyclovir/
generic substitute for dapoxetine https://salemeds24.wixsite.com/dapoxetine
hydroxychloroquine 200mg tabs https://hydroxychloroquine.mlsmalta.com/
what does cialis generic cost http://www.lm360.us/
how long does ivermectin stay in system https://ivermectin.mlsmalta.com/
where to buy priligy over the counter https://ddapoxetine.com/
hydroxychloroquine coronavirus study dose https://hydroxychloroquinee.com/
vidalista 20 mg tablet costs https://vidalista.buszcentrum.com/
what is prednisone used for treating https://bvsinfotech.com/
revatio sildenafil http://cavalrymenforromney.com/
If you would like to grow your familiarity only
keep visiting this web page and be updated with the most up-to-date information posted here.
Whats up very cool site!! Guy .. Beautiful .. Superb .. I will bookmark your blog and take the feeds additionally?
I am happy to search out so many useful info here within the put
up, we want develop extra techniques in this regard,
thank you for sharing. . . . . .
Its like you read my mind! You appear to know so much
about this, like you wrote the book in it or something.
I think that you can do with some pics to
drive the message home a bit, but instead of that, this is fantastic blog.
A great read. I’ll definitely be back. http://antiibioticsland.com/Augmentin.htm
Good day! This post couldn’t be written any better! Reading this post reminds me of my good old room mate!
He always kept talking about this. I will forward this write-up
to him. Pretty sure he will have a good read. Many thanks for sharing! http://herreramedical.org/tadalafil
If some one wishes to be updated with newest technologies after that he must be pay a visit this site and be up to date all the
time.
I loved as much as you will receive carried out right here.
The sketch is tasteful, your authored subject matter stylish.
nonetheless, you command get got an impatience over that you wish be
delivering the following. unwell unquestionably come further formerly again since exactly the
same nearly a lot often inside case you shield this hike.
–1 boro naki –3
You really make it seem so easy with your presentation but I find this topic to be actually
something that I think I would never understand. It seems too complicated and extremely broad for me.
I am looking forward for your next post, I will try to get the hang of it!
How to make money online – earnings with investment https://sites.google.com/view/site-for-investing-in-bitcoin/how-to-make-money-online-earnings-with-investment
viagra price in canada
ivermectin 3mg dose
cialis drug
viagra sildenafil 100mg
tadalafil for sale cheap
ampicilin
cialis generic 20mg
fluoxetine cap 40mg
cialis generic pills
ที่สุดของเกมที่ให้ความบันเทิงสูงสุดเต็มที่ด้วยเอฟเฟคสุดหรูทำเงินเร็วมอบเงินไว น่าจะหนีไม่พ้นสล็อตออนไลน์ ที่เหล่านักเสี่ยงโชคยกให้เป็นสุดยอดของเกมออนไลน์ UFABET แหล่งรวมเกมออนไลน์ก็ไม่พลาดที่จะจัดสล็อตออนไลน์มาให้สมาชิกอย่างจุใจ
valodea b9c45beda1 https://coub.com/stories/2621714-upd-audittiii8skupe_tech_manual_pdf
millqui b9c45beda1 https://coub.com/stories/2829328-profileschool-rrrsrr-r-davinci-resolve-16-2019-rus-chamal
hanlfat b9c45beda1 https://coub.com/stories/2805697-boris-fx-mocha-pro-2021-v8-0-3-build-19-plug-ins-for-adobe-ofx-crack-application-full-ve-top
elisnayt 79a0ff67a5 https://coub.com/stories/2813604-girls-love-black-cocks
haulat 4ea590b918 https://wakelet.com/wake/Wxaz-v-dU30oELq62_x04
vallwak ba0249fdb3 https://wakelet.com/wake/zzLbU5IuP0lSlEsREhmzC
javamal 90f3619eba https://coub.com/stories/2684936-game-pokemon-mega-evolution-apk
xangarc 7383628160 https://trello.com/c/QBBSkITv/34-cracked-libri-i-mesuesit-matematika-per-klasen-e-parezip
ellkal 7383628160 https://www.cloudschool.org/activities/ahFzfmNsb3Vkc2Nob29sLWFwcHI5CxIEVXNlchiAgMDAl8nQCAwLEgZDb3Vyc2UYgIDAoISzigoMCxIIQWN0aXZpdHkYgIDAoMm4mQgMogEQNTcyODg4NTg4Mjc0ODkyOA
dawnsalm fe98829e30 https://www.cloudschool.org/activities/ahFzfmNsb3Vkc2Nob29sLWFwcHI5CxIEVXNlchiAgMDgj47WCgwLEgZDb3Vyc2UYgIDA4Per7wkMCxIIQWN0aXZpdHkYgIDAgPPHqQgMogEQNTcyODg4NTg4Mjc0ODkyOA
kasslava fe98829e30 https://coub.com/stories/2942696-repack-civilization-call-to-power-2-no-cd-crack
goveorn fe98829e30 https://wakelet.com/wake/K5lslwPXVUPKt4iqH1lDt
fordher fe98829e30 https://coub.com/stories/3053654-free-music-video-mobile-download-12-xanche
rosialli fe98829e30 https://wakelet.com/wake/bZG_k5vokL-A4fcHOJ07k
ubolsav fe98829e30 https://trello.com/c/rZCHSa88/46-upd-xilinx-vivado-20152-crack-14
halamak d868ddde6e https://coub.com/stories/3023238-cruelzelandalibropdf81-better
garcjarq d868ddde6e https://coub.com/stories/2932381-enya-the-very-best-of-enya-deluxe-edition-2009-flac-hot
johasanj d868ddde6e https://coub.com/stories/2934503-fixed-sec-s5pc110-test-b-d-driverrar
darycha d868ddde6e https://coub.com/stories/3040970-il-re-leone-film-completo-italiano-torrent-install
lyonhen d868ddde6e https://coub.com/stories/2960019-pouce-pouce-sauve-le-zoo-jeu-pc-trackersurfer-french-11-samawhy
N-Lone-D300 | Nandrolone Decanoate buy online
chaychar d868ddde6e https://coub.com/stories/3027472-fortifycrack-katseli
carphr d868ddde6e https://coub.com/stories/3137232-asme-section-2-part-a-pdf-free-download-_verified_
melvmyca d868ddde6e https://coub.com/stories/2980732-image-line-directwave-v1-6-3-incl-keygen-r2r-repack
giosans d868ddde6e https://coub.com/stories/3035834-youtube-by-click-2-2-115-patch
chervyk d868ddde6e https://coub.com/stories/3036681-sirah-nabi-muhammad-ibnu-katzir-pdf-download-ackepeat
A lot of of what you state is astonishingly appropriate and that makes me ponder why I had not looked at this in this light previously. Your article truly did switch the light on for me as far as this specific topic goes. Nevertheless at this time there is just one factor I am not really too cozy with and while I attempt to reconcile that with the actual core theme of the position, allow me observe just what the rest of the subscribers have to say.Nicely done.
franutyn d868ddde6e https://coub.com/stories/2940717-emergency-4-dortmund-airport-mod-epub
janches d868ddde6e https://coub.com/stories/3010402-top-sardu-2-0-4-3-eam-technology-full-version
apponann d868ddde6e https://coub.com/stories/3101633-httpuploadsnackcomnmtkm7passwordtorrent-patched
manfbarn d868ddde6e https://coub.com/stories/2952400-artlantis-studio-3-serial-number-activation-code-patched
bertegby d868ddde6e https://coub.com/stories/3141448-download-fifa-13-free-12-olliqynt
saljaed b7f02f1a74 https://terlapartgepile.wixsite.com/nonmidese/post/1920-evil-returns-full-movie-in-hindi-mp4-free-download
queoce b7f02f1a74 https://lupapecasilta.wixsite.com/boothmimimitt/post/curso-full-key-pc-rar-build-patch-download
jawtrud b7f02f1a74 https://webcalisusde.wixsite.com/bravsoftrily/post/license-line-6-pod-farm-platinum-v25-rtas-vst-vst-utorrent-serial-windows
Make Money Online OVER $1,200 PER DAY with bitcoin UP! Do you know you can earn great profits by trading Bitcoin?
jenulan c0c125f966 https://clamafantit1988.wixsite.com/tertconphiva/post/duniyadari-marathi-movie-full-movie
zigfhald 4a48e5f205 https://wakelet.com/@pretinmanna24
After looking over a few of the blog posts on your web site, I honestly like your way of writing a blog. I saved it to my bookmark webpage list and will be checking back soon. Take a look at my web site too and let me know your opinion.
comleop abc6e5c29d https://coub.com/skinlowcboocon/stories
ginanfo abc6e5c29d https://coub.com/mnemimtogti/stories
deletam abc6e5c29d https://coub.com/ceugigarve/stories
ilevita 9ef30a34bc https://coub.com/korkefourpsign/stories
nedrgil 9ef30a34bc https://coub.com/soekatitar/stories
vydreta 7b17bfd26b https://coub.com/stories/3214943-install-a-chakravyuh-kannada-movie-download
kaiber 7b17bfd26b https://wakelet.com/wake/Hhkmbz2Gq2hH3K3t8I_OV
bladelv 7b17bfd26b https://trello.com/c/WF3SS70p/58-make-the-girl-dance-baby-baby-baby-uncensored-better
watcden 7b17bfd26b https://trello.com/c/1b23NPGH/31-exclusive-casper-nirvana-nb-156-wireless-driver-64-bit
renavan 7b17bfd26b https://coub.com/stories/3262017-after-earth-2013-hindi-dubbed-1080p-torrent-download-1-exclusive
rozkai 7b17bfd26b https://trello.com/c/ujBbH4a1/62-work-autocad2011xforcekeygen32bit
ezaalbi 7b17bfd26b https://wakelet.com/wake/jMRIlf2MzWsNvosFgHl-2
reesaw 7b17bfd26b https://wakelet.com/wake/MdMNFU5MLAzkx9qQGDcni
betdenz 7b17bfd26b https://coub.com/stories/2977308-minecraft-survival-test-0-30-download-breimby
jaideri 7b17bfd26b https://coub.com/stories/3366202-kaise-jiyu-tere-bin-jiya-jaye-na
ilyhay 7b17bfd26b https://coub.com/stories/3241984-download-crows-zero-1-subtitle-indonesia-720p-justale
jantam 7b17bfd26b https://wakelet.com/wake/P7pqFUuYUqNrIB0lLyrJz
lyttvall 7b17bfd26b https://trello.com/c/9HNKhB1c/31-hot-xf-mccs6-keygen
barhal 7b17bfd26b https://seesaawiki.jp/backsonchate/d/MediaMonkey%20Gold%206%2e3%2e23%2e1877%20Multilingual%20Crack%20%5fVERIFIED%5f%20Crack%20%5fVERIFIED%5f
spriromi 7b17bfd26b https://wakelet.com/wake/1P7sKM2CrnITtiE92JArY
covehan 7b17bfd26b https://www.cloudschool.org/activities/ahFzfmNsb3Vkc2Nob29sLWFwcHI5CxIEVXNlchiAgID_04eXCgwLEgZDb3Vyc2UYgICAv6OanwkMCxIIQWN0aXZpdHkYgIDA0J66zgoMogEQNTcyODg4NTg4Mjc0ODkyOA
covehan 7b17bfd26b https://www.cloudschool.org/activities/ahFzfmNsb3Vkc2Nob29sLWFwcHI5CxIEVXNlchiAgID_04eXCgwLEgZDb3Vyc2UYgICAv6OanwkMCxIIQWN0aXZpdHkYgIDA0J66zgoMogEQNTcyODg4NTg4Mjc0ODkyOA
purirai 7b17bfd26b https://coub.com/stories/3300383-imsai-arasan-23m-pulikesi-full-movie-tamil-download-hot
delaysa 7b17bfd26b https://trello.com/c/YGkAfatH/45-unmult-plugin-after-effects-cc-crack-new
bengill 7b17bfd26b https://wakelet.com/wake/fKg1LU3UpG-ZaM2kvePqA
ottalb 7b17bfd26b https://wakelet.com/wake/dSHamOeSnlaaATmzZbTrP
tavelle 7b17bfd26b https://wakelet.com/wake/YAe8mxoPr4HOb4BmR-YNr
latlisa 7b17bfd26b https://wakelet.com/wake/-CWcFS5IdZ3EmZwMszIul
uldrnoe 7b17bfd26b https://coub.com/stories/2989554-gta-amritsar-game-setup-free-download-high-quality-for-pc-for-window
whewal 7b17bfd26b https://wakelet.com/wake/soYT5IZKnja81y6RPpknF
bergod 7b17bfd26b https://seesaawiki.jp/perchfolkstadaw/d/7%207048%20Bootable%20ISO%20X%20Keygen%20%28%28EXCLUSIVE%29%29%20Full%20Zip%20Windows%2064bit
volzyr 7b17bfd26b https://coub.com/stories/3281905-kannada-suprabhatam-mp3-songs-cracked-free-downloadl
deegeor 7b17bfd26b https://coub.com/stories/3397226-hd-online-player-indian-punjabi-movies-mp4-free-downl-best
megawho 7b17bfd26b https://www.cloudschool.org/activities/ahFzfmNsb3Vkc2Nob29sLWFwcHI5CxIEVXNlchiAgMCAko7dCQwLEgZDb3Vyc2UYgICA_4T2pgsMCxIIQWN0aXZpdHkYgIDAkNujxwoMogEQNTcyODg4NTg4Mjc0ODkyOA
wendmarj 7b17bfd26b https://wakelet.com/wake/FeTITreGH0Zabug4v6CgQ
kalgreg 7b17bfd26b https://wakelet.com/wake/2ggGx1AqOlV71_NoHZ0um
alddir 7b17bfd26b https://coub.com/stories/3062499-hd-online-player-muvee-reveal-x-serial-key-work
davimar 7b17bfd26b https://wakelet.com/wake/jD0SsFdcfpp4BjwK0MyJa
modefab 7b17bfd26b https://www.cloudschool.org/activities/ahFzfmNsb3Vkc2Nob29sLWFwcHI5CxIEVXNlchiAgMCA0qvLCgwLEgZDb3Vyc2UYgIDAgJHg4wsMCxIIQWN0aXZpdHkYgIDAkOvljAgMogEQNTcyODg4NTg4Mjc0ODkyOA
mariben ec2f99d4de https://coub.com/stories/4013594-sonic-charge-permut8-v1-0-working-win-and-file-rar-download-free-macos
google maps yorum satın al hizmeti ile googledeki sıralamanızı yükseltin ve daha çok müşteri toplayın
reygpris 67426dafae https://coub.com/stories/4048548-office-1080-x264-dubbed-torrent-watch-online-free
amatale 67426dafae https://coub.com/stories/3998394-cohiba-3887-rev0-driver-win-7-32-exe-crack-pc-license-torrent
waltcail 31ebe8ef48 https://wakelet.com/wake/oH6avEJdhiLoFFWZAGFq1
jamegi 00dffbbc3c https://coub.com/stories/4258582-harry-styles-handwriting-font-pc-file-zip-free
alladene 219d99c93a https://coub.com/stories/4384676-zip-mediamon-free-64bit-activation-pc-crack
kaylband 538a28228e https://coub.com/stories/4383223-keygen-ecuaciones-diferenciales-zill-5-edicion-final-32bit-torrent-full-version-rar
taygmel 538a28228e https://coub.com/stories/4304327-mor-n-benson-recnik-2-torrent-pc-key-exe-software-full-version
zohvach 538a28228e https://coub.com/stories/4377114-x32-re-loa-rar-utorrent-software
zohvach 538a28228e https://coub.com/stories/4377114-x32-re-loa-rar-utorrent-software
daisren 538a28228e https://coub.com/stories/4257576-activator-simcity-4-64-pc-utorrent-cracked
yagmal 538a28228e https://coub.com/stories/4356994-registration-opensat-rar-full-version-x32-windows-nulled
terrchad 538a28228e https://coub.com/stories/4313601-pes-2013-indir-patch-build-64bit-full-pc-rar-registration
zacsial 538a28228e https://coub.com/stories/4276448-okami-full-version-patch-torrent-key-zip
iseawal b8d0503c82 https://coub.com/stories/4715816-serial-blaze-32bit-full-version-torrent
lyspeve b8d0503c82 https://coub.com/stories/4715009-free-hyprotech-hysys-3-1-download-patch-32-pc-rar
bapper b8d0503c82 https://coub.com/stories/4609205-epub-kandha-guru-kavasam-lyrics-in-l-book-zip-download-full-edition
reigcat b8d0503c82 https://coub.com/stories/4530427-alcatraz-dts-watch-online-dubbed-hd
অপ্রকৃত ভগ্নাংশের ক্ষেত্রে আংশিক ভগ্নাংশ প্রকাশ করার পর্বটা কিভাবে পাওয়া যাবে?
takkurs b8d0503c82 https://coub.com/stories/4537715-free-ye-maya-chesave-dual-2k-subtitles-full-english
reegper 220b534e1b https://www.kaggle.com/forrilapa/disco-deewane-movie-video-songs-in-hd-free-link
henreliz 220b534e1b https://www.kaggle.com/decvidungsven/xf-a2011-64bits-rar-top
matnat 220b534e1b https://www.kaggle.com/amacticbe/www-beastranch-com-men-and-cow
honocris df76b833ed https://www.kaggle.com/nbusaridfe/hpbiospasswordkeygendownload-new
yiesreni df76b833ed https://www.kaggle.com/muldetrchedext/guide-blu-tuttonormel-full-top-version-downloa
zeniret df76b833ed https://www.kaggle.com/zentgramdesfie/reviving-ophelia-download-portables-torrent
nenndara df76b833ed https://www.kaggle.com/tradezticma/chakkara-viyugam-movie-free-download-tor-flovalu
biawee df76b833ed https://www.kaggle.com/budsbilkompwun/descargar-bios-para-el-emulador-de-top
gavgrat df76b833ed https://www.kaggle.com/tranevinat/subaru-navigation-dvd-european-edition-v1-2008
legrsyl df76b833ed https://www.kaggle.com/enerdumag/step-up-3-final-dance-video-free-do-verified
shankri df76b833ed https://www.kaggle.com/contingtaja/tapout-xt2-torrent-iso-better
barngiod 89fccdb993 https://www.guilded.gg/edeminris-Platoon/overview/news/Gl58wB9R
gesnikk 89fccdb993 https://www.guilded.gg/tioguatylpats-Hive/overview/news/vR1nzOMl
reiljarv 89fccdb993 https://www.guilded.gg/knoctiwonters-Tigers/overview/news/NyEEXq0y
danggran 89fccdb993 https://www.guilded.gg/darxpropreisis-Cougars/overview/news/7lxYzvD6
nevewah f23d57f842 https://www.guilded.gg/matgaluness-Heroes/overview/news/4ld73K3R
naircar f23d57f842 https://www.guilded.gg/diacruntaulas-Cougars/overview/news/JRNm9BAy
harlweb f23d57f842 https://www.guilded.gg/siorathekas-Warlocks/overview/news/16n4NjxR
pinklar f23d57f842 https://www.guilded.gg/piwelzeiters-Raiders/overview/news/NyEE20Gy
rosanab f23d57f842 https://www.guilded.gg/liatajasapps-Mustangs/overview/news/A6je2wql
agrrea f23d57f842 https://www.guilded.gg/chodasualbens-Raiders/overview/news/4ldn51ky
fathrang f23d57f842 https://www.guilded.gg/sumidenjacks-Crew/overview/news/KR2B914R
wylpanc f23d57f842 https://www.guilded.gg/conripuras-Oilers/overview/news/Plq1p78l
benelyz 6be7b61eaf https://trello.com/c/BBGRvv26/77-squirtorgfanclubfreetrialcode-link
ricelys 9c0aa8936d https://tranquil-tor-35779.herokuapp.com/Half-life-includes-5-Mods-pc-game.pdf
dorianne 9c0aa8936d https://quiet-mountain-63803.herokuapp.com/download-xforce-keygen-AutoCAD-Mechanical-2018-key.pdf
reilyami cbbc620305 https://marketplace.visualstudio.com/items?itemName=term800.The-Frighteners-1996-720p-BrRip-Tamil-English-X264-BEST
panmak cbbc620305 https://meebiwheji6.artstation.com/projects/nEvYyO
wellfri 9ff3f182a5 https://www.kaggle.com/code/lesdisttanpay/eobd-facile-version-complete-keygen-new-crack
elasan 63b95dad73 https://marketplace.visualstudio.com/items?itemName=denis622.REPACK-Free-Download-Of-Bangla-Choti-By-Rosomoy-Gupta-In-B
waksol 63b95dad73 https://marketplace.visualstudio.com/items?itemName=scedecus-mi.Kid-Frost-East-Side-Story-Full-Album-Zip-2021
quiavry 63b95dad73 https://marketplace.visualstudio.com/items?itemName=Danilkouu.NBP-Freqsep-Control-For-Photoshop-11000-BEST
jamkaf 63b95dad73 https://marketplace.visualstudio.com/items?itemName=rosochka.Introduction-To-Computer-Graphics-Foley-Pdf-14
briharr 63b95dad73 https://marketplace.visualstudio.com/items?itemName=njjgnsrju.KeyshiaColeTheWayItIsfullalbumzip-Extra-Quality
niqureb ef2a72b085 https://wakelet.com/wake/Vg1uQT8YfSFdze7rCmXEw
samkava ef2a72b085 https://wakelet.com/wake/Bi5dSeF_DM7XGACN6Bvqj
amipal a60238a8ce https://coub.com/stories/4884883-driftland-the-magic-revival
niktjami baf94a4655 https://trello.com/c/YkkSdNrJ/120-descargar-mervils-a-vr-adventure-versi%C3%B3n-pirateada
onaosm baf94a4655 https://coub.com/stories/4951298-descargar-chuckie-egg-2017-challenges-version-pirateada-2022
margerv baf94a4655 https://coub.com/stories/4898529-descargar-crazy-gravity-gratuita-2022
birayaky baf94a4655 https://trello.com/c/y1C4VRqW/55-pajama-sam-3-you-are-what-you-eat-from-your-head-to-your-feet-versi%C3%B3n-pirateada
salphea baf94a4655 https://www.guilded.gg/dreamdianenols-Monarchs/overview/news/r6Bw5Qgy
Hi! I simply would like to offer you a big thumbs up for the great info you have right here on this post. I will be returning to your website for more soon.
이용이유가생기는곳 먹튀검증 안전노리터 go
Başka bir yerde bulmayacağınız gerçek kişilere ait ateşli sohbet numarası hakkında bilgi sahibi olmak için firmamızın kullanıcı dostu web ara yüzüne sahip internet sitesini sık sık ziyaret etmeniz yeterlidir.
Yabancı dizi ve film izleme yapıyorsanız, Netflix’in bu konuda en fazla tercih edilen platform olduğunu söyleyebiliriz.
Seçilen alan için hızlı ekran görüntüsü: Uygulamamız size masaüstünüzde istediğiniz alanı seçip 2 tıkla ekran görüntüsü alma imkanı sağlar.
check this Top-Rated Online Sports Betting Site in the Philippines for more information
We want our players to have the best experience possible at our online casino, that’s why we offer a simple and secure way to pay by phone. With our Deposit by Phone Bill payment method you can add funds to your online casino account quickly and easily, so you always know exactly how much you’re playing with. The deposit by phone method of playing casino games is not fixed to just mobile casino sites either. You can use this method to pay for casino sites by using your landline phone bill. Let’s say you don’t like to play at online casinos via your mobile? Don’t worry. You can still use the pay by phone method while playing on PC or tablet. As long as you have a phone of any description, you can play casino games using the pay by phone bill method. While there are clear benefits to playing slots you can pay by phone bill, there are differences to be found between different sites. So, if you want to find the best pay by phone bill casino sites, there are a set of criteria that you can use to review, rate, and compare operators. Here are the main criteria that you should consider when choosing a new pay by phone bill slots casino: https://station-wiki.win/index.php/Poker88_mobile You can find detailed instructions on cashing in on the Royal Ace no deposit bonus codes at bonuspromocode.com royal-ace-casino-no-deposit-bonus-codes . Visit BonusPromoCode for more bonus code reviews. With an unparalleled design and the most competitive odds and markets, gamble like never before with Stake’s newest way to bet. Miami Club Casino No Deposit bonus Or join now with The value of a free spin varies from one game to the next. If you play through all 35 free spins and win nothing, you are now free to claim any bonus that requires a deposit. If you have winnings, then the rollover requirement on those winnings is 5x. Note also that this bonus is non-cashable. Let’s say that you choose a slot machine where free spins are valued at $1. You play through the spins and hit a $200 jackpot. You’d have to play through $200 x 5 = $1,000 before making a withdrawal. If you did that and managed to have $50 left, you could withdraw $15 since the casino would deduct 35 x $1 = $35.
affiliate programs for fitness products
health niche affiliate marketing
online jobs for moms
organic herbal supplement affiliate programs
hormone supplements for men in the usa
next-day delivery of hormone supplements
over the counter hormonal supplements
hormone supplements without prescription with fast delivery
Legal ways to buy Actoplus without prescription Online pharmacy for diabetes Actoplus without prescription
Order Metformin online for diabetes treatment without a prescription I need some diabetes medication ASAP, but I don’t want to pay
a fortune or jump through any hoops
itnewshub.org
can i protect my blog content copyright without registering it to copyright departmen? please help?
buy generic cialis online cheap Your HCP may stop your RINVOQ treatment for a period of time if needed because of changes in these blood test results
Ceny v ubytování Appartamenti Roulette Montana Marilleva 900 se liší podle konkrétního pobytu (např. v závislosti na termínu nebo podmínkách ubytování). Pro zobrazení cen zadejte termín pobytu. V ubytování Appartamenti Roulette Montana Marilleva 900 je na výběr z několika možností (v závislosti na dostupnosti). Dostupné možnosti: 1 ložnici3 ložnice V ubytování Appartamenti Roulette Montana Marilleva 900 je na výběr z několika možností (v závislosti na dostupnosti). Dostupné možnosti: 1 ložnici3 ložnice Ubytování Appartamenti Roulette Montana Marilleva 900 je od centra destinace Mezzana vzdáleno 950 m. Check-in je v ubytování Appartamenti Roulette Montana Marilleva 900 od 16:00 a check-out je do 9:30.
https://www.yankee-bookmarkings.win/situs-pkv-games-terbaik-17
zrušeno od 30.1.2023 Peníze zdarma jsou nejpřínosnějším casinovým bonusem. Díky penězům zdarma si můžete zahrát všechny nabízené hry bez nutnosti riskovat své vlastní prostředky, ale přitom s možností vyhrát skutečné peníze. Peníze zdarma lze využít také na hrací automaty, přičemž vám nikdo nediktuje, jaké hrací automaty můžete použít a za kolik peněz byste je měli roztočit. Zřejmě nejrozšířenější typ automatů dneška. Naleznete v nich množství stylů jako například historické nebo dobrodružné a nabízí spoustu výherních linií. Sázet lze od pár korun až po několik tisíc. Mezi automaty zdarma patří mezi nejoblíbenější. Naučte (se) citovat – kniha plná užitečných rad, jak správně citovat. Vyprodáno. Například nabídka casino automaty je opravdu velká a je z čeho vybírat. Při výběru takové hry rozlišujte, kolik válců má daný automat, jak získat volné hry zdarma nebo o jaký typ automatu se jedná. Začátečníci mohou zkusit své štěstí s pár válci, pochopit systém a pak se vhrnout do ostrého hraní.
It’s in point of fact a nice and helpful piece of information. I’m glad that you shared this helpful info with us. Please stay us informed like this. Thanks for sharing.
I have read so many posts about the blogger lovers except this article is truly a pleasant piece of writing, keep it up.
Hi my family member! I want to say that this article is awesome, great written and come with almost all important infos. I’d like to peer more posts like this .
Hi, I do believe this is an excellent website. I stumbledupon it 😉 I am going to come back once again since I book-marked it. Money and freedom is the best way to change, may you be rich and continue to help other people.
Nathanial tXOMSiaMiJGQjuq 6 27 2022 37 years old, 6 1
I like the valuable information you supply for your articles. I will bookmark your weblog and check again here frequently. I am relatively certain I will be told plenty of new stuff right here! Good luck for the following!
I know this site gives quality dependent articles or reviews and additional data, is there any other web site which provides these things in quality?
Hello there! Do you know if they make any plugins to protect against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article. https://www.binance.com/id/register?ref=UM6SMJM3
I always spent my half an hour to read this blog’s posts everyday along with a cup of coffee.
First off I want to say wonderful blog! I had a quick question that I’d like to ask if you don’t mind. I was curious to know how you center yourself and clear your thoughts before writing. I have had trouble clearing my mind in getting my thoughts out. I do enjoy writing but it just seems like the first 10 to 15 minutes are generally wasted just trying to figure out how to begin. Any suggestions or tips? Kudos!
An impressive share! I have just forwarded this onto a colleague who had been doing a little research on this. And he in fact bought me breakfast because I discovered it for him… lol. So let me reword this…. Thank YOU for the meal!! But yeah, thanx for spending time to discuss this topic here on your internet site.
I don’t even know how I ended up here, but I thought this post was good. I don’t know who you are but definitely you are going to a famous blogger if you are not already 😉 Cheers!
Hey just wanted to give you a quick heads up and let you know a few of the images aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different internet browsers and both show the same results.
A fascinating discussion is worth comment. I think that you should write more on this subject, it might not be a taboo subject but usually people do not discuss such topics. To the next! All the best!!
Innovations in Tent Systems for Sustainable Camping Experiences
My relatives always say that I am wasting my time here at net, except I know I am getting knowledge everyday by reading such nice articles or reviews.
Hmm is anyone else having problems with the images on this blog loading? I’m trying to figure out if its a problem on my end or if it’s the blog. Any feed-back would be greatly appreciated.
I really love your site.. Excellent colors & theme. Did you develop this website yourself? Please reply back as I’m looking to create my very own website and want to learn where you got this from or what the theme is called. Many thanks!
All games in our database are browser-primarily based and don’t require any download or installation.
Also visit my site :: https://casino79.in/socialcasino/
Pretty nice post. I just stumbled upon your blog and wanted to say that I have really enjoyed browsing your blog posts. In any case I’ll be subscribing to your feed and I hope you write again soon!
Роскошный мужской эротический массаж Москва – тайский салон
You should take part in a contest for one of the finest sites on the net. I most certainly will recommend this site!
Wow, that’s what I was seeking for, what a information! present here at this website, thanks admin of this web site.
Howdy! This is my first visit to your blog! We are a collection of volunteers and starting a new initiative in a community in the same niche. Your blog provided us useful information to work on. You have done a outstanding job!
Simply wish to say your article is as amazing. The clearness on your submit is simply nice and i can assume you are knowledgeable in this subject. Well together with your permission allow me to seize your RSS feed to stay up to date with coming near near post. Thank you one million and please continue the rewarding work.
If you desire to get a great deal from this article then you have to apply such techniques to your won website.
I quite like looking through a post that can make people think.
Also, thank you for allowing me to comment!
У «Черной Москвы» очень удачная щеточка. Асимметричное расположение щетинок – классная фишка: короткими подбираюсь к корням и ресницам в уголках глаз, не испачкав веки, а длинными прокрашиваю и сразу разделяю ресницы по длине. Получается буквально веер – очень черный и очень объемный: Набор для макияж глаз: стойкая подводка и насыщенно-черная двухсторонняя тушь для ресниц Контурный карандаш легко наносится, не размазывается, обладает насыщенным цветом, создает четкую контурную линию. Мы ищем товары магазинов, которые продают только подлинные бренды. Никаких реплик, подделок и копий — только оригинальные товары Если есть желание поэкспериментировать со внешностью, то комбинируйте цвета в макияже, но так, чтобы это не смотрелось пошло и вульгарно. Сочетайте не только оттенки коричневого, например, светлый тон на верхнее веко, а потемнее – на нижнее. Рискните сочетать в образе тушь для ресниц коричневого цвета и насыщенного черного.
https://allods.my.games/forum/index.php?page=User&userID=122380
В ходе такой процедуры брови и ресницы получат из масла столько питательных веществ, сколько им нужно. Для протирки всего лица стоит выбирать некомедогенные жидкие масла вроде оливкового, кокосового, масла виноградных косточек. Магазин индийских товаров Витамин Е больше имеется в жирных продуктах. Наибольшее его количество есть в подсолнечном масле. Подсолнечное масло получают из семечек подсолнечника. Семечки прессуют, после чего получается масло. Масляная смесь для роста ресниц: 1 ч.л. касторового и репейного масла, несколько капель витамина Е в масле, 3 капли свежего сока алоэ. Наносите смесь на ресницы каждый вечер на 2 часа. Перед сном масло обязательно удалить. Длинные, изящно подкрученные ресницы ресницы, как у Одри Хепберн – beauty-мечта многих девушек. Если вам не посчастливилось родиться с пушистыми веерными ресницами, а наносить тушь в пять слоев кажется странным – попробуйте пять проверенных средств для их роста.
Offering the highest quality teeth whitening services, at home whitening products + professional training and certification. The use of activated charcoal started during the 20th century and was mostly recommended for tooth whitening purposes only. Activated charcoal is typically derived from the fine carbon powder obtained from burnt coconut shells, olive pits, coal, sawdust or bone char. The charcoal is passed through high heat which activates it by altering the inner structure of the charcoal, thereby making it highly porous. Chemical activation is typically preferred to the above heat processing, being more efficient and rapid. I’m on a mission to empower people everywhere with the same evidence-based, easy-to-understand dental health advice that my patients get. You can read my story here. I have been a dentist in private practice for 35 years. I graduated from the Dugoni School of Dentistry in San Francisco, CA in 1987 and am a member of the American Academy of Dental Sleep Medicine (AADSM), Academy of General Dentistry (Chicago, IL), American Academy for Oral Systemic Health (AAOSH), and Dental Board of California.
https://artistecard.com/smilebecom
You probably know that carrots can help with your eyesight, but did you know it can help with your smile? Yes, research has found eating raw carrots help scrap off the plaque from your teeth. It is a natural cleaner, to say the least. Even some people say rubbing carrot sticks directly on your teeth will help them look brighter. Strawberries help whiten your mouth in two ways. They are a great source of malic acid which is a natural enzyme. Malic acid is actually a key player when it comes to many teeth whitening tooth pastes. Also the fibers that can be found in the fruit are a natural cleanser and will remove the bad bacteria from the mouth and teeth. Teeth are naturally white. The look white because they are protected by a white external protective layer – enamel; however, once an enamel is lost then the yellowish dentin is exposed that is a clear sign of enamel erosion and it is a clear indication that you need to begin some natural teeth whitening remedies; otherwise, consult a nearest cosmetic dentist to restore your white enamel again.
I’m impressed, I must say. Rarely do I encounter a blog that’s equally educative and engaging, and let me tell you, you have hit the nail on the head. The issue is something which not enough people are speaking intelligently about. I am very happy that I found this in my search for something concerning this.
pharmacy express online
It’s awesome in favor of me to have a website, which is beneficial in favor of my knowledge. thanks admin
Hi, all the time i used to check blog posts here early in the dawn, as i like to gain knowledge of more and more.
Ja, ich bin über 18 Jahre alt. Der Spieler unternimmt bei diesem Merkur Spielautomaten eine mystische Reise durch das alte Ägypten. Auf bis zu 10 Gewinnlinien dreht sich alles um den antiken Sonnengott Horus. Als Wild-Symbol ergänzt er alle Gewinnlinien zum größtmöglichen Linien-Gewinn. Dieser 5-Walzen-Slot sorgt für anhaltende Spannung und besticht durch hohe Gewinnchancen. „Eye of Horus“ ist auch zu Übungszwecken erst einmal ohne Echtgeld im Demo-Modus spielbar. Erst rund 10 Jahre später kam es dann zur Eingliederung des Angebots in die adp Gauselmann GmbH, die heute adp Merkur GmbH heißt. Merkur Gaming ist im Besitz zahlreicher Gesellschaften, darunter nicht nur hierzulande, sondern auch in Polen, den Niederlanden oder auch Mexiko, um nur einige zu nennen. Merkur Gaming ist somit ein wichtiger Baustein der Gauselmann Gruppe, denn das Unternehmen kümmert sich um die Entwicklung und den Vertrieb lokaler sowie digitaler Geldspielautomaten.
https://cs.astronomy.com/members/a4wmplg140/default.aspx
Hier muss man ganz klar das Spiel Book of Ra nennen. Dieser Klassiker ist eines der beliebtesten Spiele und vielleicht der bekannteste Slot überhaupt. Das Thema und das besondere Spielprinzip mit dem zusätzlichen Bonussymbol wurde unzählige Male von anderen Providern kopiert. Book of Ra hat eine ganze Welle von nachfolgenden Ägypten-Slots ausgelöst, deren Einfluss noch heute sichtbar ist. Die Antwort darauf erklärt wohl gleichsam die einfache Grafik. Es wurde vom Hersteller bewusst versucht, den Book of Ra Spielautomaten aus den 80er Jahren digital zu übertragen und den größtmöglichen Wiedererkennungswert des schon in den landbasierten Casinos erfolgreichen und beliebten Spiels zu wahren. Gewiss war im Erscheinungsjahr des Online Slots Book of Ra technisch bereits mehr möglich. Besonders der Klang erinnert uns an die alten Geräte aus den Kneipen und Spielhallen und ist als nostalgische Reminiszenz zu verstehen.
I am extremely impressed with your writing skills and also with the layout on your blog. Is this a paid theme or did you customize it yourself? Either way keep up the nice quality writing, it’s rare to see a nice blog like this one these days.
Pretty section of content. I just stumbled upon your weblog and in accession capital to assert that I acquire in fact enjoyed account your blog posts. Any way I’ll be subscribing to your augment and even I achievement you access consistently rapidly.
Thank you for some other informative website. Where else may just I am getting that kind of info written in such a perfect means? I have a project that I am simply now operating on, and I have been at the glance out for such information.
Every weekend i used to visit this website, as i want enjoyment, since this this web site conations in fact pleasant funny information too.
Hi mates, pleasant post and nice arguments commented here, I am truly enjoying by these.
Thank you for any other wonderful article. Where else may anyone get that kind of information in such a perfect method of writing? I have a presentation next week, and I am at the look for such information.
Abby He wants to talk frankly with you and show you something, you will like it. Click Here: http://www.google.com/amp/s/teens.page.link/go
Very rapidly this site will be famous among all blogging people, due to it’s good posts
It’s great that you are getting ideas from this piece of writing as well as from our discussion made at this place.
Сайт 1xBet считается одним из самых надежных онлайн букмекеров России. БК 1xBet пользуется огромной популярностью среди пользователей из РФ и стран СНГ. Лучшие коэффициенты ставок на спорт, лучшие онлайн игры, слоты казино и еще много других плюсов букмекерской конторы заслуживают внимания. Промокод 1xBet на сегодня и бесплатно. Для постоянных игроков БК 1хбет регулярно проводятся различные акции,промокод на 1xbet в рамках которых любая положенная на счет сумма (в рамках определенных пределов) будет увеличена (обычно в два раза). Для вывода подарочных денег требуется поставить деньги несколько раз на события с определенными условиями. Ставки на спорт 2023 – Получить бонус 1xbet и промокод на 32500 рублей от официального сайта 1хбет. Бонус для новых игроков! При регистрации в 1xbet новые клиент получает бонус в размере 32500 рублей. Зарегистрироваться в 1XBet. Бонус действует только для новых пользователей 1xbet.