আমরা আজকে বিচ্ছিন্ন ফাংশনের লেখচিত্রের একটি অসাধারণ বৈশিষ্ট্য নিয়ে কথা বলব, তা হল অসীমতট রেখা। তাহলে কথা না বাড়িয়ে মূল আলোচনা শুরু করে ফেলা যাক। 😀
অসীমতট হল সেই রেখা যা কোনো একটি বক্ররেখাকে অসীমের কোনো বিন্দুতে স্পর্শ করে বা বক্ররেখাটি যেই রেখার দিকে আগাতে থাকে অথবা বক্ররেখার limiting value যেই রেখার দিকে যেতে থাকে।
সহজ কথায়, কোনো একটি রেখা আর বক্ররেখার মধ্যবর্তী দূরত্ব যদি ক্রমশ কমতে থাকে এবং অসীমে তা শূন্যের কাছাকাছি হয় তাহলে ওই রেখাটিকে ওই বক্ররেখার অসীমতট রেখা বলে।
 অসীমতট থেকে কোনো একটি ফাংশনের লেখচিত্রের অসীমে ব্যাবহার সম্পর্কে জানা যায়। লেখচিত্র আঁকাতে অসীমতট নির্ণয় করা অনেক সময় একটা গুরুত্বপূর্ণ প্রাথমিক ধাপ হিসেবে কাজ করে।
অসীমতট থেকে কোনো একটি ফাংশনের লেখচিত্রের অসীমে ব্যাবহার সম্পর্কে জানা যায়। লেখচিত্র আঁকাতে অসীমতট নির্ণয় করা অনেক সময় একটা গুরুত্বপূর্ণ প্রাথমিক ধাপ হিসেবে কাজ করে।
তিন ধরনের অসীমতট রেখা আছেঃ আনুভূমিক (horizontal), উল্লম্ব (vertical) আর তির্যক (oblique)
আনুভূমিক অসীমতট:
আনুভূমিক অসীমতট হল আনুভূমিক রেখা যা x অক্ষের সমান্তরাল এবং বক্ররেখার ফাংশনের ভুজ অর্থাৎ x এর মান অসীমের দিকে যেতে থাকলে এর কোটি অর্থাৎ functional value ওই রেখার দিকে অগ্রসর হতে থাকে।
অর্থাৎ y = c রেখাটি y = f(x) বক্ররেখার আনুভূমিক অসীমতট হবে যদি

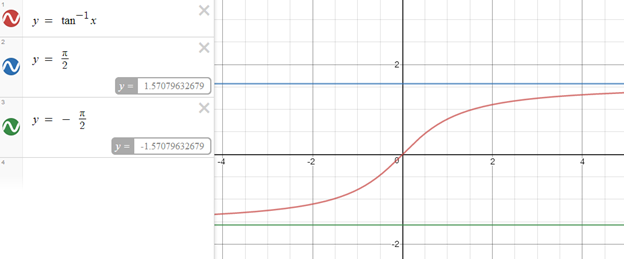

উল্লম্ব অসীমতট:
উল্লম্ব অসীমতট হল উল্লম্ব রেখা যা y অক্ষের সমান্তরাল এবং বক্ররেখার ফাংশনের ভুজ অর্থাৎ x এর যেকোনো মানের জন্যে এর কোটি অর্থাৎ functional value অসীমের দিকে যেতে থাকে অর্থাৎ ওই রেখার দিকে অগ্রসর হতে থাকে।
অর্থাৎ x = c রেখাটি y = f(x) বক্ররেখার উল্লম্ব অসীমতট হবে যদি

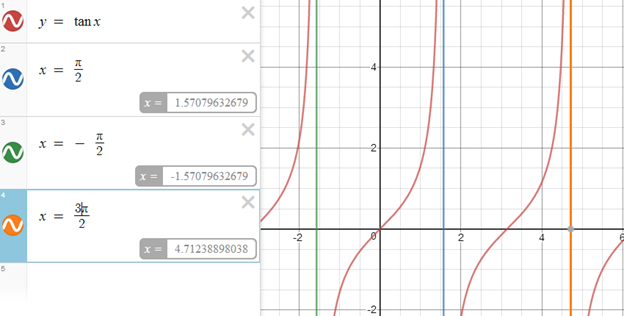

তির্যক অসীমতটঃ
আরেক ধরণের অসীমতট রেখা আছে যা x বা y কোনো অক্ষেরই সমান্তরাল নয়। তাই এই ধরণের অসীমতটকে বলা হয় তির্যক অসীমতট। অর্থাৎ তির্যক একটা রেখা যখন অসীমে কোন বক্ররেখাকে স্পর্শ করে বা বক্ররেখা থেকে ঐ তির্যক রেখার দূরত্ব যদি কমতে থাকে এবং অসীমে তা প্রায় শুন্যের কাছাকাছি হয় তাহলে ঐ তির্যক রেখাটি ঐ বক্ররেখার অসীমতট।
অর্থাৎ y = mx + c যেখানে m , রেখাটি y = f(x) বক্ররেখার তির্যক অসীমতট হবে যদি

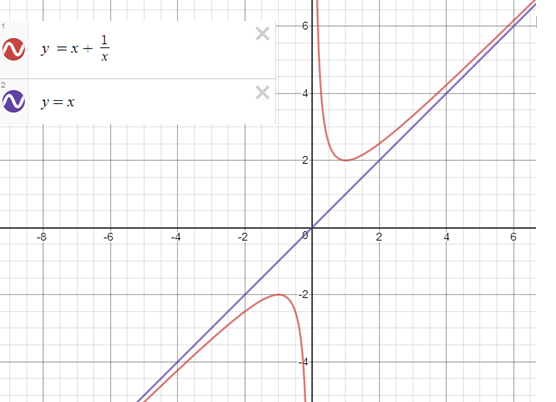

বহুপদী ভগ্নাংশের অসীমতট রেখাঃ
একটি বহুপদী ভগ্নাংশের সর্বোচ্চ একটি আনুভূমিক অসীমতট রেখা, সর্বোচ্চ একটি তির্যক অসীমতট রেখা এবং অনেকগুলো উল্লম্ব অসীমতট রেখা থাকতে পারে।
কিছু উদাহারণ দিয়ে ব্যাপারটা পরিষ্কার করে দেখা যাক।

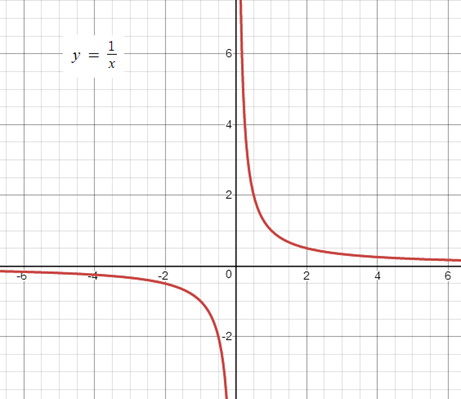
এর একটি আনুভূমিক অসীমতট রেখা আছে যা হল y = 0 রেখাটি বা x অক্ষ এবং একটি উল্লম্ব অসীমতট রেখা আছে যা হল x = 0 রেখাটি বা y অক্ষ।
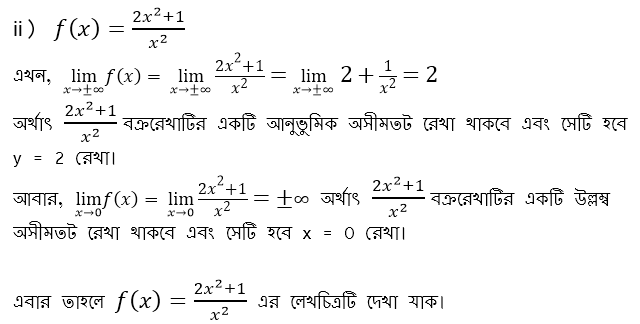
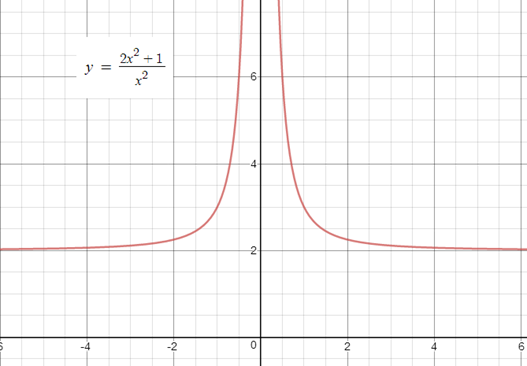 এর একটি আনুভূমিক অসীমতট রেখা আছে যা হল y = 2 রেখাটি এবং একটি উল্লম্ব অসীমতট রেখা আছে যা হল x = 0 রেখাটি বা y অক্ষ।
এর একটি আনুভূমিক অসীমতট রেখা আছে যা হল y = 2 রেখাটি এবং একটি উল্লম্ব অসীমতট রেখা আছে যা হল x = 0 রেখাটি বা y অক্ষ।

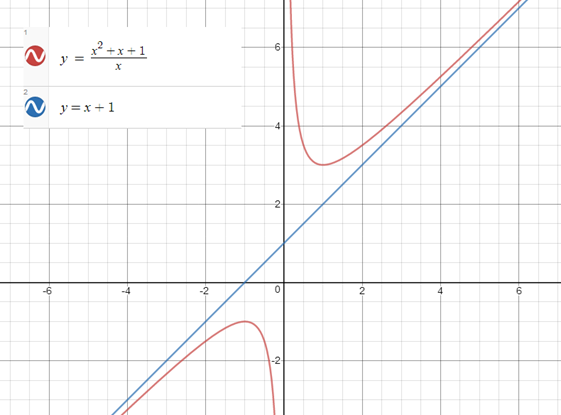 এর একটি তির্যক অসীমতট রেখা আছে যা হল y = x + 1 রেখাটি এবং একটি উল্লম্ব অসীমতট রেখা আছে যা হল x = 0 রেখাটি বা y অক্ষ।
এর একটি তির্যক অসীমতট রেখা আছে যা হল y = x + 1 রেখাটি এবং একটি উল্লম্ব অসীমতট রেখা আছে যা হল x = 0 রেখাটি বা y অক্ষ।

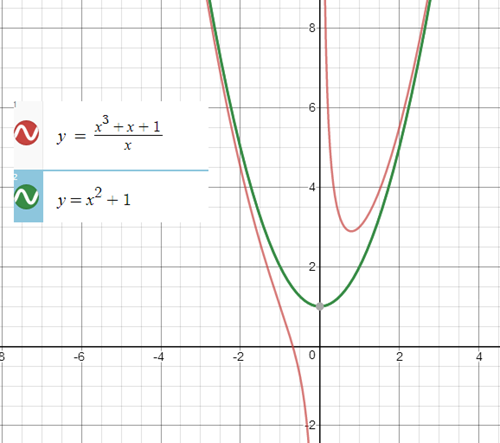
এর একটি উল্লম্ব অসীমতট রেখা আছে যা হল x = 0 রেখাটি বা y অক্ষ। কিন্তু কোনো তির্যক বা আনুভূমিক অসীমতট রেখা নেই। এর একটি অসীমতট বক্ররেখা (curvilinear asymptote) আছে, যেই বক্ররেখাটি একটি পরাবৃত্ত।
বহুপদী ভগ্নাংশের অসীমতট রেখার ধারণাটিকে একটি ছকের সাহায্যে প্রকাশ করা হলঃ
| লবের মাত্রা – হরের মাত্রা | আনুভূমিক বা তির্যক অসীমতট রেখার ধরণ |
| < 0 |
y = 0 রেখা |
| = 0 |
y = “লব ও হরের মুখ্য সহগের অনুপাত” রেখা |
| = 1 |
y = “লবকে হর দিয়ে ভাগ করলে প্রাপ্ত ভাগফল” রেখা |
| > 1 | কোনো আনুভূমিক বা তির্যক অসীমতট রেখা পাওয়া যাবে না কিন্তু অসীমতট বক্ররেখা (curvilinear asymptote) পাওয়া যাবে। |
কেবল মাত্র বহুপদী ভগ্নাংশের হর শূন্য হলেই উল্লম্ব অসীমতট রেখা পাওয়া যাবে। এক্ষেত্রে উল্লেখ্য যে লব আর হরে যদি কোনো সাধারণ উৎপাদক থাকে তাহলে সাধারণ উৎপাদক ভাগ দেয়ার পর যে সরলরূপ থাকবে তার হর শূন্য হলে উল্লম্ব অসীমতট রেখা পাওয়া যাবে।
যেমনঃ ![]() এর উল্লম্ব অসীমতট রেখা পাওয়া যাবে x = 0 এবং x = 1 এ, x = 2 তে কোনো উল্লম্ব অসীমতট রেখা পাওয়া যাবে না।
এর উল্লম্ব অসীমতট রেখা পাওয়া যাবে x = 0 এবং x = 1 এ, x = 2 তে কোনো উল্লম্ব অসীমতট রেখা পাওয়া যাবে না।
এক পলকে লেখচিত্রটি দেখে নেয়া যাক।
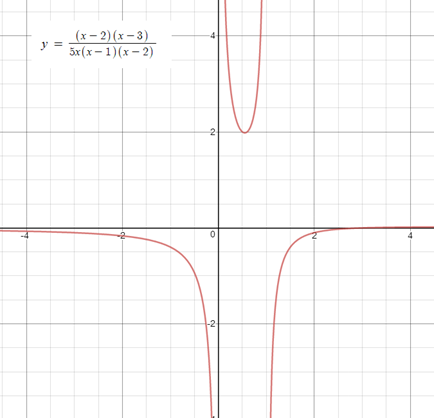
আরো কিছু উদাহারণ দেখা যাক।
![]() এর লেখচিত্রটি দেখা যাক।
এর লেখচিত্রটি দেখা যাক।
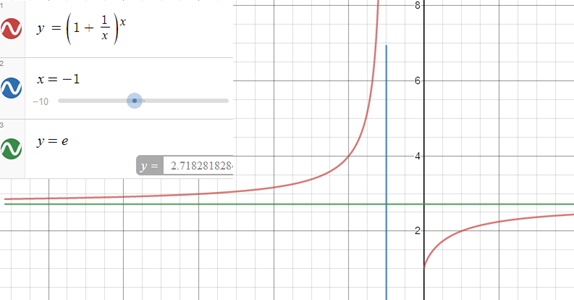
এর একটি আনুভূমিক অসীমতট y = e রেখা আর একটি উল্লম্ব অসীমতট x = -1 রেখা।
![]() এর লেখচিত্রটি দেখা যাক।
এর লেখচিত্রটি দেখা যাক।
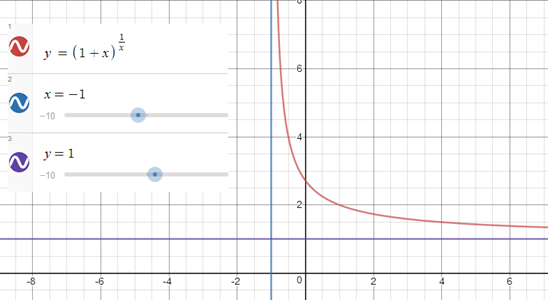 এর একটি আনুভূমিক অসীমতট y = 1 রেখা আর একটি উল্লম্ব অসীমতট x = -1 রেখা।
এর একটি আনুভূমিক অসীমতট y = 1 রেখা আর একটি উল্লম্ব অসীমতট x = -1 রেখা।
![]() এর লেখচিত্রটি দেখা যাক।
এর লেখচিত্রটি দেখা যাক।
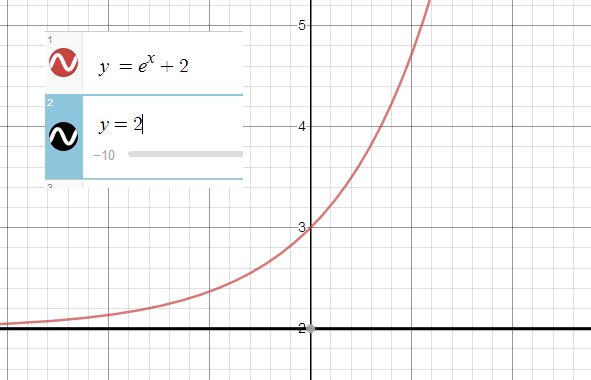 এর একটি আনুভূমিক অসীমতট y = 2 রেখা।
এর একটি আনুভূমিক অসীমতট y = 2 রেখা।
![]() এর লেখচিত্রটি দেখা যাক।
এর লেখচিত্রটি দেখা যাক।
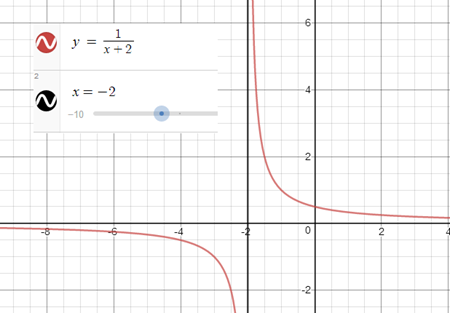 এর একটি উল্লম্ব অসীমতট x = -2 রেখা।
এর একটি উল্লম্ব অসীমতট x = -2 রেখা।
![]() এর একটি উল্লম্ব অসীমতট হল x = 0 রেখা। তাহলে
এর একটি উল্লম্ব অসীমতট হল x = 0 রেখা। তাহলে ![]() এর একটি উল্লম্ব অসীমতট হল x = 0-2 = -2 রেখা।
এর একটি উল্লম্ব অসীমতট হল x = 0-2 = -2 রেখা।
অর্থাৎ x = a যদি f(x) এর একটি উল্লম্ব অসীমতট রেখা হয় তাহলে x = a+h হবে f(x-h) এর একটি উল্লম্ব অসীমতট রেখা।
![]() এর লেখচিত্রটি দেখা যাক।
এর লেখচিত্রটি দেখা যাক।
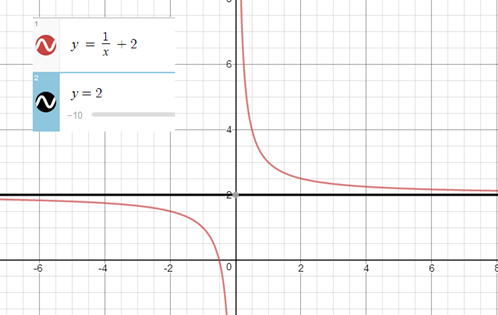 এর একটি আনুভূমিক অসীমতট y = 2 রেখা।
এর একটি আনুভূমিক অসীমতট y = 2 রেখা।
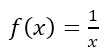 এর একটি আনুভূমিক অসীমতট হল y = 0 রেখা। তাহলে
এর একটি আনুভূমিক অসীমতট হল y = 0 রেখা। তাহলে ![]() এর একটি আনুভূমিক অসীমতট হল y = 0+2 = 2 রেখা।
এর একটি আনুভূমিক অসীমতট হল y = 0+2 = 2 রেখা।
অর্থাৎ y = a যদি f(x) এর একটি আনুভূমিক অসীমতট রেখা হয় তাহলে y = a+h হবে f(x) + h এর একটি আনুভূমিক অসীমতট রেখা।
![]() এর লেখচিত্রটি দেখা যাক।
এর লেখচিত্রটি দেখা যাক।
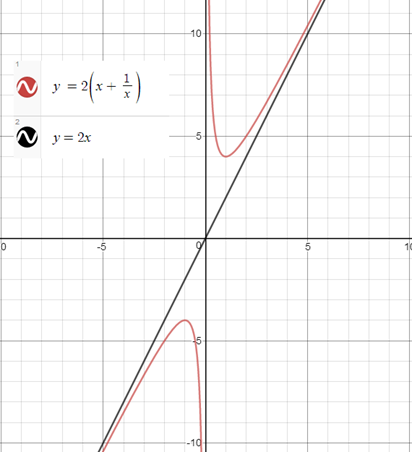
এর একটি তির্যক অসীমতট y = 2x রেখা।
![]() এর একটি তির্যক অসীমতট হল y = x রেখা। তাহলে
এর একটি তির্যক অসীমতট হল y = x রেখা। তাহলে ![]() এর একটি তির্যক অসীমতট হল y = 2x রেখা।
এর একটি তির্যক অসীমতট হল y = 2x রেখা।
অর্থাৎ y = ax+b যদি f(x) এর একটি তির্যক অসীমতট রেখা হয় তাহলে y = c(ax+b) হবে cf(x) এর একটি তির্যক অসীমতট রেখা।
কনিকের (অধিবৃত্তের) অসীমতটঃ

কিছু উদাহারণ দেখা যাক।

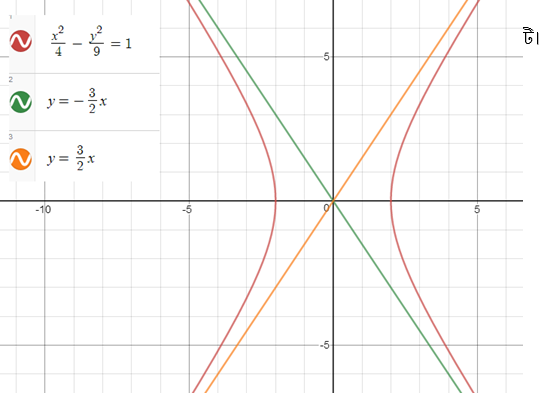

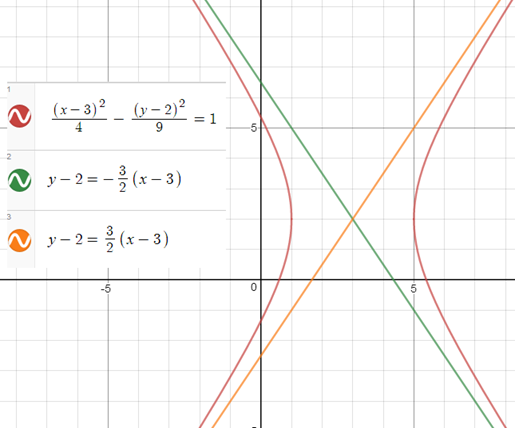
এখন তাহলে দেখা যাক যেকোনো অধিবৃত্তের জন্যে অসীমতট রেখার সমীকরণ কি হবে।

একটি উদাহারণ দেখা যাক তাহলে বিষয়টি পরিষ্কার হবে।
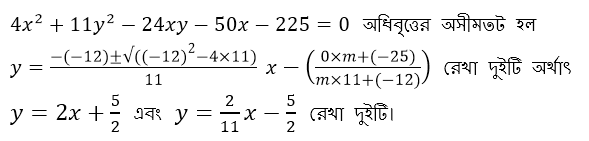

curvilinear asymptote:
কোনো কোনো ফাংশনের লেখচিত্রের অসীমতট সরলরেখা না হয়ে বক্ররেখা হতে পারে, তখন ওই অসীমতট কে বলা হয় curvilinear asymptote.
একটি উদাহারণ দিয়ে তাহলে ব্যাপারটা পরিষ্কার করে ফেলা যাক।
![]() এই ফাংশনটির কথাই ধরা যাক।
এই ফাংশনটির কথাই ধরা যাক।
এর ক্ষেত্রে
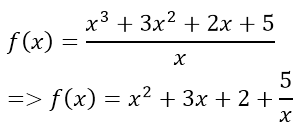
x এর মান অসীমের দিকে যেতে থাকলে 5/x প্রায় শুন্যের কাছাকাছি হতে থাকে অর্থাৎ f(x) প্রায় x2 + 3x + 2 এর কাছাকাছি হতে থাকে।
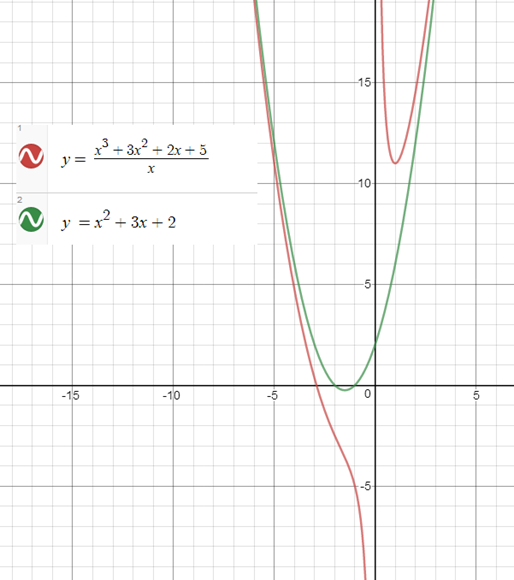
অর্থাৎ f(x)এর একটি উল্লম্ব অসীমতট রেখা হল x = 0 রেখা বা y অক্ষ। কিন্তু এর কোনো আনুভূমিক বা তির্যক অসীমতট রেখা নেই, যে অসীমতট আছে তা একটি পরাবৃত্ত যেটি হল যা একটি বক্ররেখা। এই পরাবৃত্তীয় অসীমতট হল f(x) এর curvilinear asymptote.
এবার তাহলে লেখচিত্রটি এক পলকে দেখে ফেলা যাক।
আজ তাহলে এ পর্যন্তই। আশা করি অসীমতট সম্পর্কে ধারণা পেয়েছ এবং বিষয়গুলো বুঝতে পেরেছো। কোনো কিছু বুঝতে না পারলে অবশ্যই জানাবে কিন্তু। 😀
দেখা হবে আবার সামনে নতুন কোনো বিষয় নিয়ে। 🙂

Amazing depiction.
অসীমতটের ব্যবহার করে কোনো রিয়েল লাইফ প্রবলেম সলভ করে দেখালে আরো ইন্টারেস্টিং হত লিখাটা।
মহাবিশ্ব ক্রমেই সম্রসারিত হচ্ছে।অসীমতট এর সাহায্যে কোন গ্রহের পূর্বে অবস্থান বা পরের অবস্থান।এবং কোন সংঘর্ষের সম্ভবনা নির্নয় করা হয়