শেষমেশ আবার ফিরে এলাম। নতুন কিছু লেখা হয় নি বেশ অনেক দিন। কাজেই, এসেই যখন পড়েছি তখন শুরু করাই যাক।
শিরোনাম দেখেই বুঝতে পারছো, আজকে আমরা আমাদের চিরপরিচিত চার্লসের সূত্র(Charles’ Law) নিয়ে কিছু একটা পড়ার চেষ্টা করবো।
আমরা যখন Ideal Gas বা আদর্শ গ্যাস নিয়ে লেখাপড়া করতে যাই আমাদের বেদবাক্যের মতো তিনটা সূত্র পড়ে যেতে হয়। বয়েলের সূত্র, চার্লসের সূত্র, রেনোর কিংবা গে লুস্যাক’র(যা- ই বলি না কেন) চাপীয় সূত্র। আর তাদের প্রত্যেকের বিবৃতি খুবই সোজা। যেমন ধরো, বয়েলের ক্ষেত্রে আমরা বলি P এবং V পরস্পর ব্যস্তানুপাতিক; চার্লসের ক্ষেত্রে V এবং T সমানুপাতিক; আর গে লুস্যাকের ক্ষেত্রে P আর T পরস্পর সমানুপাতিক।
কিন্তু সমস্যাটা বাঁধে যখন আমাদের বইয়ে বিবৃতির নামে কি এক বিদঘুটে কাহিনী শোনানো হয়। কি শোনানো হয় আমিই বরং বলে দিইঃ “স্থির চাপে কোনো নির্দিষ্ট ভরের গ্যাসের আয়তন প্রতি ডিগ্রি সেলসিয়াস তাপমাত্রা হ্রাস বা বৃদ্ধির জন্য শূন্য ডিগ্রি সেলসিয়াস তাপমাত্রার আয়তনের 1/273 অংশ হ্রাস বা বৃদ্ধি পায়”। কি আজগুবি কথা বলো তো। কোথায় “V এবং T সমানুপাতিক” আর কোথায় এ বিদঘুটে বিবৃতি আর তার সাথে আজগুবি একটা ম্যাথম্যাটিক্যাল ব্যাখ্যা। কাজেই চলো,
এর মাহাত্ম্য বের করা যাক।
বিদঘুটে বিবৃতির গাণিতিক ব্যাখ্যাঃ
তা জানার জন্য আমাদের উচ্চতর গণিত প্রথম পত্রের সরলরেখা অধ্যায়ের কিছু Concept কাজে লাগবে। (যদিও উচ্চতর গণিত বলা হচ্ছে তারপরও Concept টা মোটেও উচ্চতর কিছু না কিন্তু। অতএব, ঘাবড়াবার কিছু নেই)
এখন দেখো, এ বিবৃতির সাথে একটা গ্রাফ দেয়া থাকে। আমরা এ গ্রাফ দেখেই আমরা এর মাহাত্ম্যটুকু পুরোপুরি বুঝে নিবো।
গ্রাফটা দেখো তো; এরকম না দেখতে?
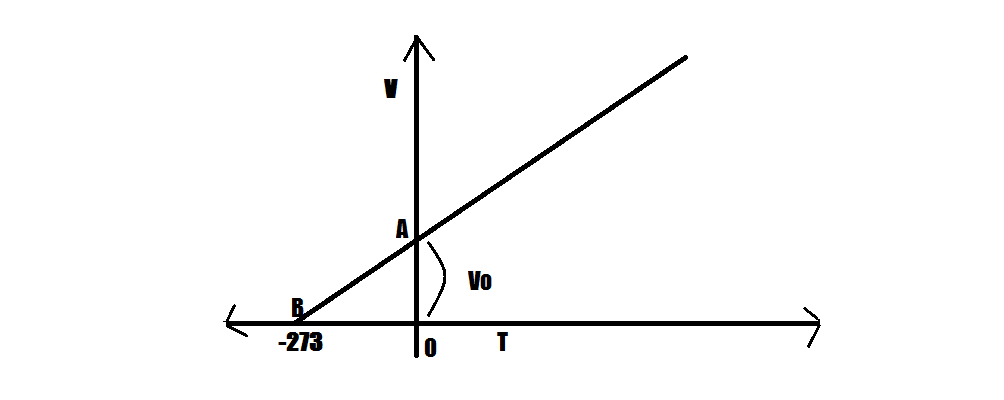
Charles law
এখন মনোযোগ দাও। x অক্ষে তুমি দেখতে পাচ্ছো V অর্থাৎ আয়তনকে আর y অক্ষে তুমি দেখতে পাচ্ছো T অর্থাৎ তাপমাত্রাকে।
এবার তোমাকে গণিতের সেই সরলরেখার বিখ্যাত সমীকরণে নিয়ে যাই
![]()
আচ্ছা, x অক্ষে যেহেতু তুমি T কে দেখতে পাচ্ছো x এর জায়গাতে T কে বসিয়ে দাও আবার y অক্ষে যেহেতু তুমি V কে দেখতে পাচ্ছো কাজেই y এর জায়গাতে তুমি V কে বসিয়ে দাও। দেখো তো, দেখতে নিচের সমীকরণের মতো হয় কি না!
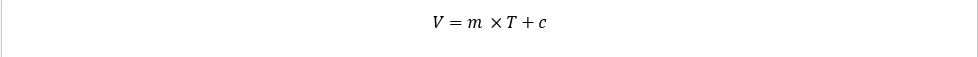
এখন তুমি বলতে পারো, এ আবার কেমন কথা। x আছে দেখে সেখানে T বসিয়ে দিবো আবার যেখানে y আছে সেখানে V কে বসিয়ে দিবো। বললেই হয়ে গেলো নাকি। [আসলে, এই ফাঁকে তোমাকে জানিয়ে রাখি, আমি যে কাজটা করলাম এটা গ্রাফ এনালাইসিস করার খুব গুরুত্বপূর্ণ একটা Tool. তোমার পরীক্ষাতে অনেক সময় প্রশ্ন আসে না, যে, অমুক সূত্রের গ্রাফ কিরকম সেখানে তুমি সূত্রের রাশিমালায় x আর y বসিয়ে দেখবে, সূত্রটা দেখতে কিরকম লাগে। সেটা যদি দেখতে সরলরেখার মতো হয় তাহলে সেটা সরলরেখার গ্রাফ, আবার যদি দেখো সেটা পরাবৃত্তের মতো দেখতে তাহলে সেটা পরাবৃত্তের গ্রাফ আর অন্যকিছুর মতো হলে সেটা অন্যকিছুর গ্রাফ। যাক গে! অনেক কথা বলে ফেললাম!]
এখন তুমি আমাদের গ্রাফের দিকে আরেকটু তাকাও। দেখো, x অক্ষে T কে প্লট করা হয়েছে যেখানে 0^0 সেলসিয়াসে (অর্থাৎ, মূলবিন্দুতে)আমাদের সরলরেখা y অক্ষকে যে বিন্দুতে ছেদ করেছে সেটা অবশ্যই 0^0 সেলসিয়াসে আয়তন(আর আমরা তার নাম দিয়েছি V knot; V এর নিচে ছোট্ট করে একটা শূন্য 😛 )। কারণ y অক্ষে আমরা আয়তনকে প্লট করেছি।
এবার আসো, আমরা আমাদের সমীকরণে যে m নামের রাশিটা আছে তাকে ব্যাখ্যা করে ফেলি। তোমরা ইতিমধ্যেই জানো m হচ্ছে সরলরেখার ঢাল নির্দেশ করে। এখন ঢাল বের করার জন্য তুমি যে সূত্র জানো আমিই তোমাকে বলে দিই সেটা হল
![]()
এখানে, তুমি দেখতে পাবে OAB ত্রিভুজে tanθ=V_0/273 (খেয়াল করো তো, আমি এখানে “–” sign omit করেছি। কেন বলতে পারবে?)
এখন তুমি মানগুলো Inject করে দাও আমাদের সমীকরণে। দেখো তো, সেটা নিচের সমীকরণের মতো কি নাঃ
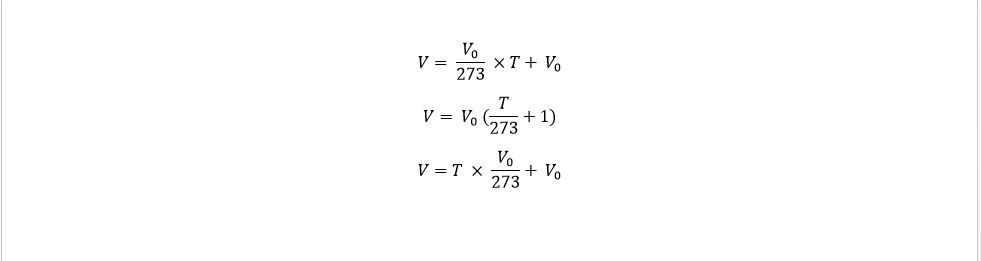
হুররে! আমরা পেয়ে গেলাম আমাদের বিবৃতির সাথে বইয়ে যে ম্যাথমেটিক্যাল ব্যাখা দেয়া তা কোত্থেকে এলো তার প্রমাণ। এবার আমরা মেলাবো তা কিভাবে “V এবং T সমানুপাতিক” এই কনসেপ্টকে প্রকাশ করে।
খেয়াল করো, নিচের লেখাটা একটা নিখাদ constant! এবার তুমিই বলো আমরা একে “V এবং T সমানুপাতিক” না বলে উপায় আছে?!
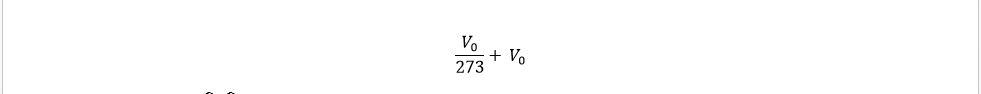
এবারে আসো বিবৃতির ব্যাখায়ঃ
স্থির চাপ আর নির্দিষ্ট ভর কেন রাখতে হবে তা চিন্তা করার দায়িত্ব আমি তোমার উপর ছেড়ে দিলাম। এখন দেখো, বিবৃতি কি বলছে? বিবৃতি বলছে, “প্রতি ডিগ্রি সেলসিয়াস তাপমাত্রা হ্রাস বা বৃদ্ধির জন্য শূন্য ডিগ্রি সেলসিয়াস তাপমাত্রার আয়তনের 1/273 অংশ হ্রাস বা বৃদ্ধি পায়”।
তো চলো, আমরা ধাপে ধাপে এগোই,
শূন্য ডিগ্রি সেলসিয়াস তাপমাত্রায় আয়তনের 1/273 অংশ মানে নিচের লেখা না?
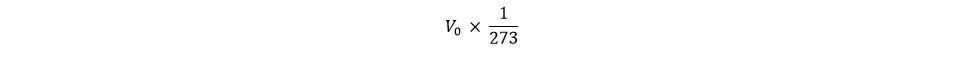
তাহলে T ডিগ্রি তাপমাত্রা পরিবর্তনের জন্য আয়তনের পরিবর্তন নিচের লেখাটা হবে না?
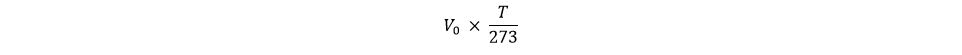
কিন্তু…কিন্তু… আমরা কিন্তু এতোক্ষণ T ডিগ্রিতে আয়তন কতো হবে তা বের করি নি? তাহলে কি বের করেছি? আমরা বের করেছি T ডিগ্রিতে “পরিবর্তন” কতো হবে তা! কাজেই মোট আয়তন এখন কতো হবে বলো তো?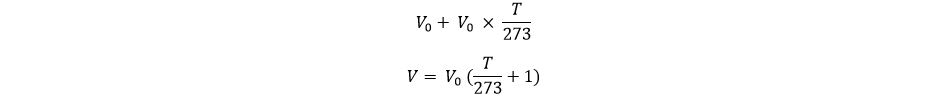
কি চমৎকার! তাই না?! কারণ এটাই তো তুমি ম্যাথম্যাটিক্যাল ব্যাখ্যায় পেয়েছিলে!
এখন বোঝা গেলো তো কিভাবে এই গাণিতিক ব্যাখ্যা আর বিদঘুটে বিবৃতিটি খাপে খাপে মিলে যায়!
যদি না বুঝে থাকো তাতে আর সমস্যা কি! আরেকবার পড়েই দেখো না!
