ধরে নাও একদিন সকালে তুমি রাস্তায় হাঁটতে হাঁটতে  ঢুকে পড়লে কোন এক সরু, নির্জন গলিতে। গলিটির যেই প্রান্ত দিয়ে তুমি ঢুকেছ, তার ঠিক একই সময় বিপরীত প্রান্ত থেকে আরেকজন মানুষ এসে তোমার দিকে হাঁটা শুরু করলো। তখন হয়তো  তোমার দৃষ্টিকোণ থেকে মনে  হবে যে সেই লোকটিই তোমার দিকে এগিয়ে আসছে, লোকটির মনে হবে যে তুমিই তাঁর দিকে হেটে যাচ্ছ, আবার পাশের বাড়ির বারান্দা থেকে তোমাদের দুজনকেই দেখতে থাকা আরেকজনের দৃষ্টিতে মনে হবে তোমরা দুজনই একজন আরেকজনের দিকে এগিয়ে যাচ্ছ। কারো দৃষ্টিকোণ থেকেই কেউ ভুল নয়, আবার কারো উত্তরই কারো সাথে মিলছে না। তবে এমনটি হওয়ার কারণ কি? আসলে কে কার দিকে এগুচ্ছে?

স্থিরতা ও গতিশীলতার আপেক্ষিক বৈশিষ্ট্য নিয়ে এমন সব প্রশ্নের উত্তর আমরা  খুঁজবো আমাদের আজকের এই পর্বে।

তাহলে চল, এবার একেবারে প্রথম থেকেই শুরু করা যাক।

প্রতিদিন আমরা আমাদের চারপাশে এমন অনেক কিছুই দেখি যা কোন একটি নির্দিষ্ট জায়গা দখল করে বসে থাকে প্রায় অনন্তকাল জুড়ে, অন্তত যতক্ষণ না পর্যন্ত আমরা জোর করে সেগুলিকে সরিয়ে না দেই তাদের নিজের জায়গা থেকে। আবার, সেই সাথে এমন অনেক কিছুই (এবং অনেক মানুষও রয়েছে বটে :p) রয়েছে যারা কোনভাবেই এক জায়গায় স্থির থাকতে পারে না, অন্তত যতক্ষণ না পর্যন্ত আমরা সেগুলিকে থামানোর জন্য কোন ব্যবস্থা নেওয়া হয়।

প্রথম শ্রেণির জিনিসগুলোর উদাহরণ হিসেবে ধরে নিতে পারো তোমার টেবিলকে, যেটিকে তুমি ধাক্কা দিয়ে সরিয়ে না দেওয়া পর্যন্ত তা তোমার ঘরের সেই একই কোণেই বসে থাকবে, অথবা টেবিলের উপর রাখা তোমার খাতাটিকে, বাতাস এসে যার পাতাগুলিকে উলটিয়ে না নিলে তা ঠিক সেই একি অবস্থাতেই পরে থাকবে দিনের পর দিন (বিশেষ করে আমাদের মত ফাঁকিবাজ ছাত্র হলে তো কথাই নেই, তুমি সেই খাতাটিকে খুলেও দেখবে না, পরীক্ষার আগের রাত পর্যন্ত 😉 )। এইসব বস্তুর অবস্থানকে আমরা বলি স্থির, একটি নির্দিষ্ট সময়কালের মধ্যে এদের অবস্থানের কোন পরিবর্তন হয় না। সহজ ভাষায় বললে, তারা যেখানে ছিল, সেখানেই থাকে।

দ্বিতীয় যেই শ্রেণির কথা বলা হয়েছে, সেগুলিকে আমরা বলতে পারি গতিশীল, যেমন একটি চলন্ত বাস, একটি ঘুরন্ত ফ্যানের ব্লেড, নির্দিষ্ট কক্ষপথে পরমাণুর নিউক্লিয়াসকে আবর্তন করতে থাকা একটি ইলেকট্রন, অথবা তোমার টেবিলের উপর বীরদর্পে হেটে যাওয়া একটি পিঁপড়া। বাস হোক, ইলেকট্রন হোক, হোক তা একটি ছোট্ট পিঁপড়া, তাদের সবার সম্বন্ধেই একটি কথা প্রযোজ্য, আর তা হল যে তাদের অবস্থান পরিবর্তনশীল। কাল অতিক্রান্ত হওয়ার সাথে সাথে তাদের অবস্থানেরও পরিবর্তন ঘটে। এক কথায়, তারা গতিশীল।

আর এই গতিশীলতারই কিছু মৌলিক ব্যাপার-স্যাপার নিয়ে আমরা আলোচনা করার চেষ্টা করবো এই সিরিজে, যার শুরু হল আজ এই লেখাটির মাধ্যমে।

এবার একটু ফিরে তাকানো যাক।

০.১ টেবিলটিকে স্থির ঘোষণা করার ইতিকথা

পদার্থের গতিশীলতা আর স্থিরতা নিয়ে যতগুলি উদাহরণ দিলাম এই পর্যন্ত, তা সবগুলিই কিন্তু আপেক্ষিক। অর্থাৎ, তারা স্থির নাকি গতিশীল, তা নির্ভর করবে তোমার নিজের দৃষ্টিকোণের উপর।

খুব সহজ সরলভাবে চিন্তা করলে হয়তো তোমার মনে হতে পারে যে তোমার রুমে যেই টেবিলটি রয়েছে, তা সব দৃষ্টিকোণ থেকেই স্থির অবস্থানে রয়েছে। সত্যিই তো, টেবিলটিকে যেই দেয়ালের সাথে গা ঘেঁষিয়ে রাখা হয়েছে, সেই দেয়াল থেকে তো তা এক চুল পরিমাণও নড়ছে না।

যদি তাই মনে হয়, তবে এবার আরেকটু বৃহত্তর পরিসরে চিন্তা করা যাক ব্যাপারটা নিয়ে। আগেই বলেছি, গতিশীলতা আর স্থিরতা আপেক্ষিক ব্যাপার। কোন বস্তু স্থির নাকি আপেক্ষিক, তা কিন্তু সম্পূর্ণভাবেই নির্ভর করবে তার অবস্থানকে আমরা কিসের সাপেক্ষে বিবেচনা করছি, তার উপর। তোমার ঘরের সাপেক্ষে চিন্তা করলে তোমার টেবিলটি স্থির অবস্থাতেই রয়েছে। এক্ষেত্রে তুমি তোমার নিজের ঘরকেই ধরে নিয়েছ তোমার প্রসঙ্গ কাঠামো (Frame Of Reference)  হিসেবে। অর্থাৎ তোমার টেবিলের গতিপ্রকৃতিকে আমরা বিবেচনা করেছি যেই কাঠামোর সাপেক্ষে, তা হল তোমার ঘর।

এবার Frame Of Reference বা Reference Frame নিয়ে একটু সংক্ষেপে বলে নেই। Reference Frame হল একটি মাপকাঠি, যার সাহায্যে কোন বস্তুর অবস্থান ও কাল নিয়ে ধারণা পাওয়া যায়। গতিশীলতা পরিমাপের ক্ষেত্রে আমরা সাধারণত একটি নির্দিষ্ট সিস্টেমকে ধরে নেই, যার সাপেক্ষেই পরিমাপ করা হয় একটি বস্তুর অবস্থান, গতি, ত্বরণ ইত্যাদি। এর আগের উদাহরণটিতে যেমন আমরা রুমের সাপেক্ষেই টেবিলের অবস্থান ও গতি প্রকৃতিকে মেপে এসেছি, সেভাবেই যে কোন Reference Frame-কে আমরা ব্যবহার করতে পারি যেকোনো বস্তুর অবস্থান পরিমাপ করতে।  উল্লেখ্য, Reference Frame-কে যে সবসময় কোন বাহ্যিক অবকাঠামো হতে হবে, এমন কিন্তু কোন কথা নেই। আমরা আমাদের মনের মাধুরি মিশিয়ে মহাবিশ্বের যেকোনো স্থানেই একটি প্রসঙ্গ কাঠামো ধরে নিতে পারি, এমন নয় যে সেটি আমাদের ঘরের মত তার একটি সুগঠিত অবকাঠামো থাকতে হবে।

আরেকটি গুরুত্বপূর্ণ কথা, প্রত্যেক Reference Frame-এরই থাকে একটি মূলবিন্দু বা Reference Point, যার সাপেক্ষে বাকি সকল বিন্দুকেই একটি নির্দিষ্ট স্থানাংক দিয়ে চিহ্নিত করা যায়। Reference Point এর কাজ একটি দ্বি-মাত্রিক লেখচিত্রের (০,০) বিন্দুর মত, এবং ওই মূলবিন্দুকে ঘিরে রাখা সকল বিন্দুকে নিয়েই গঠিত হয় আমাদের Reference Frame।

আমাদের Frame Of Reference কিন্তু একমাত্রিক, দ্বিমাত্রিক, ত্রিমাত্রিক, এমনকি আরও বেশি মাত্রারও হতে পারে, ব্যাপারটি সম্পূর্ণই নির্ভর করবে কোন পদার্থের গতিশিলতাকে প্রকাশ করতে যতগুলি মাত্রার co-ordinate system-এর প্রয়োজন হয় তার উপর।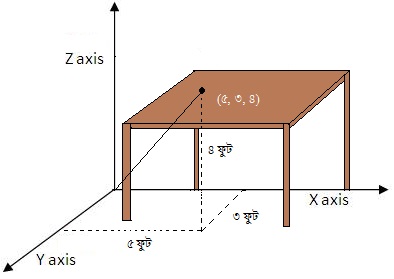

 

অতএব, আমরা যদি আমাদের ঘরের মেঝের একটি কোণ কে আমাদের Reference Point ধরে নেই, এবং যদি আনুমানিকভাবে সেই কোণটি থেকে আমাদের টেবিলের যেকোন একটি বিন্দুর দূরত্ব হয় রুমটির দৈর্ঘ্য বরাবর ৫ ফুট, প্রস্থ বরাবর ৩ ফুট ও উচ্চতা বরাবর ৪ ফুট; তবে আমরা এই Reference frame এর সাপেক্ষে ওই বিন্দুটির স্থানাংক দাড়ায় (৫, ৩, ৪)।

 

এখন যদি আমরা ৫ মিনিট পর এসে আবার এই একি টেবিলেরই একই বিন্দুর স্থানাংক মাপতে যাই, তবে আমরা ঠিক একই ফলাফলই পাব। এর অর্থ হল, আমাদের বর্তমান reference frame অনুযায়ী টেবিলটি স্থির অবস্থাতেই থেকে গেছে এই ৫ মিনিট জুড়ে।

 

বিঃ দ্রঃ কেউ যদি এই ৫ মিনিটের মধ্যে রুমে ঢুকে টেবিলটি নাড়াচাড়া করে আবার ঠিক আগের অবস্থানে রেখে দেয়, তাহলেও কিন্তু আমরা বলব যে বস্তুটি ৫ মিনিট সময়ের মধ্যে স্থির অবস্থানেই রয়েছে।

 

০.২ ঘূর্ণায়মান  পৃথিবী, ঘূর্ণায়মান টেবিল

 

আচ্ছা, নিজের ঘরই যখন স্বয়ং Frame of Reference, তখন টেবিলটি যে স্থির, তা বুঝার জন্য তো আমাদের প্রতিদিনের অভিজ্ঞতাই যথেষ্ট, co-ordinate systems নিয়ে এত প্যাঁচাল না পাড়লেও হয়। 😀 কিন্তু এবার একটু চিন্তা করে দেখ, যেই ঘরটির সাপেক্ষে আমরা এতক্ষণ টেবিলটির অবস্থান মাপলাম, সেই ঘরটিই কি পুরোপুরি স্থির? আমরা জানি যে, পৃথিবী তার নিজ অক্ষ বরাবর ঘুরছে, এবং একটি নির্দিষ্ট কক্ষপথ বরাবর তা সূর্যের চারপাশেও ঘুরে বেরায়। পৃথিবী নিজেই গতিশীল, এবং পৃথিবীর উপর প্রতিটি জিনিসও পৃথিবীর সাথে সাথেই নড়ছে, including তোমার ঘর, তোমার টেবিল, তোমার টেবিলের উপর রাখা খাতা, তুমি নিজে এবং আরও কত কি! পৃথিবী ঘুরছে, তার সাথে ঘুরছে পৃথিবীর উপর সবকিছুই। পৃথিবীর সাথেই সেগুলি প্রতি ২৪ ঘণ্টায় একবার করে পৃথিবীর অক্ষকে আবর্তন করে, সৌর জগতের বাকি সকল গ্রহের মতই তারা বছরজুড়ে সূর্যের চারপাশে ঘুরে। সুতরাং, আমরা যদি পৃথিবীপৃষ্ঠের বাইরে কোন বিন্দুকে আমাদের  Reference Point ধরে নিয়ে একটি Reference frame চিন্তা করি, তখন দেখা যাবে তোমার ঘরের টেবিলটিও সেই Reference frame -এ গতিশীল।

 

ঠিক একইভাবে চিন্তা করে দেখ, একজন পথচারীর সাপেক্ষে একটি চলন্ত বাস অবশ্যই গতিশীল, তবে বাসের ভিতরে থাকা একজন যাত্রীর সাপেক্ষে বাসটি কিন্তু স্থির অবস্থাতেই রয়েছে। বরং সেই যাত্রী যদি বাসের জানালা দিয়ে বাইরের কোন এক পথচারীকে দেখে, তবে তার দৃষ্টিতে সেই পথচারীই বরং বাসটির সাপেক্ষে উলটো দিকে বাসটির সমান গতিতে ছুটছে।

 

লেখাটির প্রথমদিকে আমরা যেই টেবিলের উপর রাখা খাতাটির কথা বলছিলাম, সেই খাতাটিকে যদি তুমি তোমার ব্যাগের ভিতর ঢুকিয়ে তোমার স্কুল/কলেজের দিকে হাটা শুরু কর, তাহলে হয়তো পথে দারিয়ে থাকা একজনের সাপেক্ষে সেই খাতাটি গতিশীল থাকবে, তবে তোমার ব্যাগের সাপেক্ষে কিন্তু খাতাটি স্থির অবস্থান-ই বজায় রাখবে।

 

এই সব উদাহরণের মাধ্যমে যেই একটি ব্যাপারকে আমরা স্পষ্ট করে বলার চেষ্টা করছি, তা হল যে কোন পদার্থের গতিশীলতা ও স্থিরতা সম্পূর্ণই আপেক্ষিক ব্যাপার। কোন কিছুর অবস্থানকে আমরা মাপি একটি নির্দিষ্ট বিন্দুর বা Reference Point এর সাপেক্ষে, অবস্থানের পরিবর্তনের হার (গতি)-কেও সেভাবেই মাপা হয়, একইভাবে মাপা হয় গতির পরিবর্তনের হার(ত্বরণ)-কেও। গতিশীলতা নিয়ে আমরা যত আলোচনা করবো, সবকিছুতেই এই ব্যাপারটি মাথায় রাখা প্রয়োজন, যে আমরা কীসের সাপেক্ষে গতি, সরণ, ত্বরণ, ইত্যাদি মেপে যাচ্ছি।

 

০.৩. বাস্তব জগতে আপেক্ষিক পরিমাপ

 

আমরা এখন যা করবো তা হল গতিশীলতা ও স্থিরতার আপেক্ষিক চরিত্রকে ব্যবহার করে আমাদের বাস্তব জগতে দেখা কিছুটা আজব(!) কিন্তু অত্যন্ত স্বাভাবিক দৈনন্দিন ঘটনাকে বিশ্লেষণ করার চেষ্টা। চল, একে একে শুরু করা যাক সেগুলি।

০.৩.১ বাসের ভিতর লাফঝাপ!!!

পদার্থের গতিশীলতা নিয়ে আলোচনা করতে গিয়ে বাসের কথা আসলেই বারবার উঠে আসছে। কখনো আমরা কথা বলছি বাসের ভিতরের মানুষজনদের নিয়ে, কখনো তার বাইরের। কেনই বা নয়? Reference Frame –কে ঘন ঘন পরিবরতন করার এমন সুযোগ বাসের মত আর কোথায়ই বা পাওয়া যায়? :3

যাইহোক, ধর তুমি একটি বাসে দাঁড়িয়ে আছো। বাসটি চলন্ত থাকা অবস্থাতেই ধর তুমি একেবারে সোজাসোজি উপরের দিকে লাফ দিলে। একটু খেয়াল করে দেখ, বাসটি কিন্তু চলন্ত। তুমি যেই জায়গা থেকে লাফ দিয়েছিলে, নামার পর বাসটি আর সেই জায়গায় নেই। আর তুমি লাফ দেওয়ার পর কিন্তু বাসের কোন অংশের সাথেই তোমার সংস্পর্শ নেই। অর্থাৎ, সাধারণভাবে চিন্তা করলে যা হওয়ার কথা তা হল, তুমি তোমার নিজের জায়গাতেই থাকবে, আর বাস তার গতিতেই এগিয়ে যাবে। সুতরাং, নামার পর বাসের মেঝেতে তোমার অবস্থান আরও পিছিয়ে যাওয়ার কথা। কিন্তু বাস্তবে দেখা যাবে মেঝের ঠিক যেই জায়গা থেকে তুমি লাফ দিয়েছিলে, ঠিক সেই জায়গাতেই আবার এসে নামবে, যদি না এর মধ্যে বাসটির গতি হ্রাস বা বৃদ্ধি না পায়। অর্থাৎ তোমার অবস্থান বাসের মেঝে বরাবর এক চুল পরিমাণও নড়বে না।

 

কিন্তু কেন এমনটি হয়?

 

বিষয়টিকে আমার এবার রেফারেন্স ফ্রেমের আলোকে চিন্তা করে দেখি। অনেকেই হয়তো খেয়াল করে ফেলতে পারো যে বাসের মেঝে বরাবর অবস্থান পিছিয়ে যাওয়ার হিসেব কষবার সময় আমরা একাধিক রেফারেন্স ফ্রেমকে মিশিয়ে ফেলেছি। ঘটনাটিতে প্রথমে বাসকে রেফারেন্স ফ্রেম ধরে বিবেচনা কর। বাইরের মানুষের দৃষ্টিতে বাসটি চলন্ত বা স্থির-যেটাই থাকুক না কেন, বাসটির ভিতরের যাত্রীর সাপেক্ষে কিন্তু বাসটি স্থির অবস্থাতেই রয়েছে, এবং যাত্রীটিও সেই বাসের সাপেক্ষে স্থির অবস্থানে রয়েছে। অতএব, এক্ষেত্রে যাত্রীটি কেবল বাসটির উপর উলম্বভাবে লাফিয়েছে, এবং বাসটির মেঝে বরাবর যাত্রীটির অবস্থানের পরিবর্তন হওয়ারও কোন কারন নেই, যদি আমরা কেবল বাস ও যাত্রীর মধ্যকার (আপেক্ষিক) গতিশীলতাকে মাপতে যাই।

 

বাসের বাইরে থেকে কোন একটি রেফারেন্স ফ্রেমের মাধ্যমেও ব্যাপারটি ব্যাখ্যা করা যায়। সেক্ষেত্রে যাত্রীটির পৃথিবীর পৃষ্ঠ বরাবর বেগ সবসময়ই বাসের সমান, এবং লাফ দেয়ার মাধ্যমে যাত্রীটি কেবল উলম্ব তল বরাবর একটি বেগ সৃষ্টি করছে, যার ফলে পুরো প্রক্রিয়ার সময় সে তার অবস্থান পরিবর্তন করছে পরাবৃত্তাকার পথে।

 

তবে এটি নিয়ে আরও বিস্তারিত আলোচনা ও গাণিতিক বিশ্লেষণ আমরা ভবিষ্যতে অন্য একটি পর্বে করবো বলে আশা করছি। আপাতত এইটুকু বুঝতে পারলেই হবে যে বাস ও যাত্রীর মধ্যকার আপেক্ষিক গতি মাপার জন্য আমরা স্বয়ং বাসটিকেই একটি রেফারেন্স ফ্রেম ধরে নিতে পারি, এবং তার সাপেক্ষেই বাসের/যাত্রীর গতিশীলতাকে পরিমাপ করতে পারি।

 

০.৩.২ পশ্চিমমুখী বিমানের গল্প

 

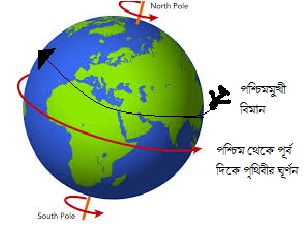
আমরা জানি পৃথিবী প্রতিনিয়তই নিজের অক্ষের উপর আবর্তন করছে। এবং পৃথিবীর আবর্তনের দিক পশ্চিম থেকে পূর্ব দিক বরাবর। এবার চিন্তা করা যাক, ধর একটি বিমান পূর্ব দিক থেকে পশ্চিম দিক বরাবর যাচ্ছে, সেক্ষেত্রে কি তার একই রুটে চলা আরেকটি পূর্বমুখী বিমানের চাইতে অপেক্ষাকৃত কম সময় লাগার কথা? (যেহেতু নীচের ভূমি পশ্চিমমুখী বিমানটির দিকে এগিয়ে আসার কথা, এবং পূর্বমুখী বিমানটি থেকে দুরে সরে যাওয়ার কথা।)

না, ব্যাপারটা একদমই সেরকম নয়। প্রথম কথা, পৃথিবীর মাধ্যাকর্ষণ বল থেকে  বিমানটিও মুক্ত নয়, এবং দ্বিতীয়ত, এখানেও আপেক্ষিকতার প্রসঙ্গটি উঠে আসা বাঞ্ছনীয়। একটি বিমানের বেগ বলতে আমরা যা বুঝি, তা মাপা হয় পৃষ্ঠ বরাবর তার অবস্থান পরিবর্তনের হারের মাধ্যমে। এক্ষেত্রে আমাদের রেফারেন্স ফ্রেম হল পৃথিবীপৃষ্ঠ নিজেই। পৃথিবী ঘুরছে, সাথে ঘুরছে বিমানটিও, তবে বিমানটি তার নিজস্ব বেগের সাহায্যে ভূমি বরাবর তার নিজের অবস্থানকে পাল্টাচ্ছে। পৃথিবীর নিজের গতিশীলতা বিমানটির আপেক্ষিক গতির উপর কোন প্রভাব রাখছে না, ঠিক যেমন বাসের গতিশীলতা বাসের যাত্রীর (মেঝের উপর) শেষ গন্তব্যের উপর কোন প্রভাব ফেলেনি।

বিমান ও যাত্রী-দুটির ক্ষেত্রেই যা প্রযোজ্য তা হল তাদের আপেক্ষিক গতি রেফারেন্স ফ্রেমের গতির উপর নির্ভরশীল নয়। রেফারেন্স ফ্রেম যদি হয় পুরো পৃথিবী, তবে সেই পৃথিবী কোনদিকে কিভাবে ঘুরছে, তার প্রভাব বিমান ও  ভূমির আপেক্ষিক গতির উপর পড়বে না। এক্ষেত্রে বিমান পশ্চিমমুখীই হোক বা পূর্বমুখীই হোক, তার গন্তব্যে পৌঁছতে কতক্ষণ সময় লাগবে তা কেবল নির্ভর করবে তার নিজের গতির উপর, পৃথিবীর ঘূর্ণনের উপর নয়।

 

 

০.৩.৩ একটি সহজ সমস্যা

 

আমরা অনেকেই হয়তো স্রোতের প্রতিকূলে এবং অনুকূলে যাওয়ার সময় একটি নৌকোর বেগ যথাক্রমে অমুক এবং তমুক হলে স্রোতহীন নদীতে নৌকোর বেগ কত এবং নদীর স্রোতের বেগ কত হবে-এই ধরণের অংক করে এসেছি। এবার এই সমস্যারই একটি ভিন্নরূপ দেখব আমরা।

 

ধরো, একটি নৌকোর বেগ ঘণ্টায় ৭ কিঃমিঃ । অপরদিকে স্রোতের বেগ ঘণ্টায় ৩ কিঃমিঃ । তাহলে নৌকোর মাঝির সাপেক্ষে নদীর পানির বেগ কত যখন নৌকোটি যথাক্রমে স্রোতের প্রতিকূলে ও অনুকূলে যায়? এক্ষেত্রে নৌকোর মাঝিই আমাদের রেফারেন্স পয়েন্ট। সমস্যাটির সমাধান আমি তোমাদের উপরেই ছেড়ে দিচ্ছি, কোন প্রশ্ন বা সমস্যা হলে যেকোন সময় আমাদের সাথে যোগাযোগ করতে পারো নির্দ্বিধায়! 🙂

 

আজ এই পর্যন্তই। সম্ভব হলে গতিবিদ্যার মৌলিক কনসেপ্ট ও সেগুলির গাণিতিক ব্যাখ্যা নিয়ে আলোচনা করবো আমরা পরবর্তী পর্বগুলিতে। আশা করি এটি কেবল শুরুর শেষ, শেষের শুরু নয়। 😀