সম্ভাবনা শব্দটি আমরা প্রতিদিনই বুঝে বা না বুঝে বিভিন্ন কাজে ব্যবহার করি। যেমন, আবহাওয়া পূর্বাভাসে বলা হয় আজ বজ্র সহ বৃষ্টিপাতের সম্ভাবনা রয়েছে। কিংবা খেলার সময় আমরা বলি, আজকে বাংলাদেশ জেতার সম্ভাবনা অনেক বেশি। আবার পরীক্ষার আগের দিন হয়তো বলি, আজকে “হয়তো” পাশ করা হবে না – অর্থাৎ পাশ করার সম্ভাবনা খুবই কম। কিন্তু সমস্যা হল, আমাদের এসব কথা সম্ভাবনা বেশি বা কম – এর মধ্যেই সীমাবদ্ধ। এর কোনো সাংখ্যিক মান এখানে বলা যায় না। সম্ভাব্যতার সাংখ্যিক মান নির্ণয় এবং এর তাৎপর্য নিয়েই আমাদের এই সিরিজ!
তো শুরু করার আগেই আমাদের কিছু টার্ম সম্পর্কে জেনে নিতে হবে। যেমন,
দৈব পরীক্ষা
ধর, তোমার কাছে একটি কয়েন আছে, যার দুইটি পিঠ – হেড এবং টেল। তুমি জান যে, এটি নিক্ষেপ করা হলে এতে কেবল হেড এবং টেল আসা সম্ভব। এর বাইরে কোনো কিছু হওয়া সম্ভব না। কিন্তু তুমি নিশ্চিত ভাবে বলতে পারবে না যে একবার নিক্ষেপে হেড আসবে নাকি টেল আসবে। অথবা ধর তোমার কাছে ৫২ টা তাস আছে। এখন এখান থেকে একটা বেছে নিলে সম্ভাব্য কী কী কার্ড তোমার কাছে আসতে পারে, তুমি তা জান। কিন্তু তুমি নিশ্চিতভাবে বলতে পার না যে, একটা কার্ড বেছে নিলে সেটা হরতন হবে বা রুইতন!
দৈব পরীক্ষা বলতে এই ব্যাপারটাকেই বোঝায়, যখন আমরা পরীক্ষায় কী কী ফলাফল হতে পারে, সেটা জানি। কিন্তু একবার পরীক্ষা দিলে কী হবে সেটা নিশ্চিত ভাবে বলতে পারি না। এখানে কয়েন নিক্ষেপ করা কিংবা একটি তাস বেছে নেওয়া হল এক একটি দৈব পরীক্ষা।
ঘটনা
ধর, তোমার কাছে একটি ছক্কার গুটি আছে। তুমি এটি নিক্ষেপ করলে (এটি হল দৈব পরীক্ষা), এবং ছক্কার গুটিতে আসলো ৪। এখন একবার ছক্কা নিক্ষেপ করে ৪ পাওয়াটা হল একটি ঘটনা। আবার খেয়াল কর, ৪ একটি জোড় সংখ্যা। তাহলে, এক্ষেত্রে জোড় সংখ্যা পাওয়াও একটি ঘটনা। আবার তুমি চাইলে বলতে পার, ৪-এর গুনিতক পাওয়া একটি ঘটনা। কিংবা ৮-এর গুণনীয়ক পাওয়া! একটি দৈব পরীক্ষার ঘটনাগুলোকে এভাবে অনেকভাবেই ব্যাখ্যা করা যায়।
কিতাবী ভাষায় ঘটনার সংজ্ঞা হল, কোনো পরীক্ষার ফলাফল বা ফলাফলের সমাবেশকে ঘটনা বলে।
সমসম্ভাব্য ঘটনাবলী
তুমি যখন একটি মুদ্রা নিক্ষেপ কর, তোমাকে যদি জিজ্ঞেস করা হয়, হেড আসার সম্ভাব্যতা বেশি নাকি, টেল? তোমার উত্তর হবে দুইটা আসার সম্ভাবনাই একই। এক্ষেত্রে মুদ্রা নিক্ষেপের ব্যাপারটা হল একটি সমসম্ভাব্য ঘটনা। বল তো, মুদ্রা নিক্ষেপের পরীক্ষাটা কখন অসমসম্ভাব্য হয়ে যাবে? এটা হতে পারে যদি তুমি মুদ্রার যেকোনো একটি পিঠে কিছু ভর সংযুক্ত করে দাও! আবার ছক্কার গুটি নিক্ষেপের পরীক্ষা অসমসম্ভাব্য হয়ে যেতে পারে, যদি তুমি এর যেকোনো একটা ধার ভোতা করে দাও। (খেয়াল কর, আমি হয়ে যাবে বলছি না, বলছি হয়ে যেতে পারে। অর্থাৎ এখানেও সম্ভাব্যতা। জগতে সবই সম্ভাব্যতার খেলা! 😀 )
পরস্পর বিচ্ছিন্ন ঘটনাবলী
যখন একটি নিরপেক্ষ মুদ্রা নিক্ষেপ করা হয়, তখন হেড আসতে পারে, টেলও আসতে পারে। কিন্তু কখনো হেড আসলে একইসাথে টেল আসতে পারে না। অর্থাৎ হেড অথবা টেল – যেকোনো একটা অবশ্যই আসবে। কিন্তু দুইটা একসাথে কখনোই আসবে না। এটা হল পরস্পর বিচ্ছিন্ন ঘটনার উদাহারণ।
কেতাবী ভাষায়, কোনো পরীক্ষায় যদি একটা ঘটনা ঘটে যাওয়া সাপেক্ষে অন্য ঘটনাগুলো ঘটতে না পারে, তবে উক্ত ঘটনাগুলোকে বলে পরস্পর বিচ্ছিন্ন ঘটনা।
অনুকূল ফলাফল
ধর তুমি চাও একটি ছক্কার গুটি নিক্ষেপের ফলে জোড় আসার সম্ভাবনা বের করতে। এখন ছক্কার গুটি নিক্ষেপে মোট ফলাফল ৬ টি – ১, ২, ৩, ৪, ৫, ৬। জোড় সংখ্যা আছে ৩ টি – ২, ৪ এবং ৬। অর্থাৎ তোমার কাঙ্ক্ষিত ঘটনার স্বপক্ষের আছে ৩ টা। এই ৩ টি ঘটনাই হবে এক্ষেত্রে তোমার অনুকূল ফলাফল। আবার, যদি বলা ছক্কা নিক্ষেপের ফলে ৬-এর চেয়ে কম আসার সম্ভাবনা কত, সেক্ষেত্রে অনুকূল ফলাফল হবে ৫ টি – ১, ২, ৩, ৪, ৫।
খেয়াল কর, এখানে জোড় আসার ব্যাপারটা হল ঘটনা, আর ২, ৪, ৬ একেকটা আসার ব্যাপারটা হল ফলাফল। অর্থাৎ ফলাফলের সমাবেশ হল ঘটনা।
কেতাবী ভাষায়, কোনো পরীক্ষায় একটি ঘটনার স্বপক্ষের ফলাফলকে উক্ত ঘটনার অনুকূল ফলাফল বলে।
নমুনাক্ষেত্র ও নমুনা বিন্দু
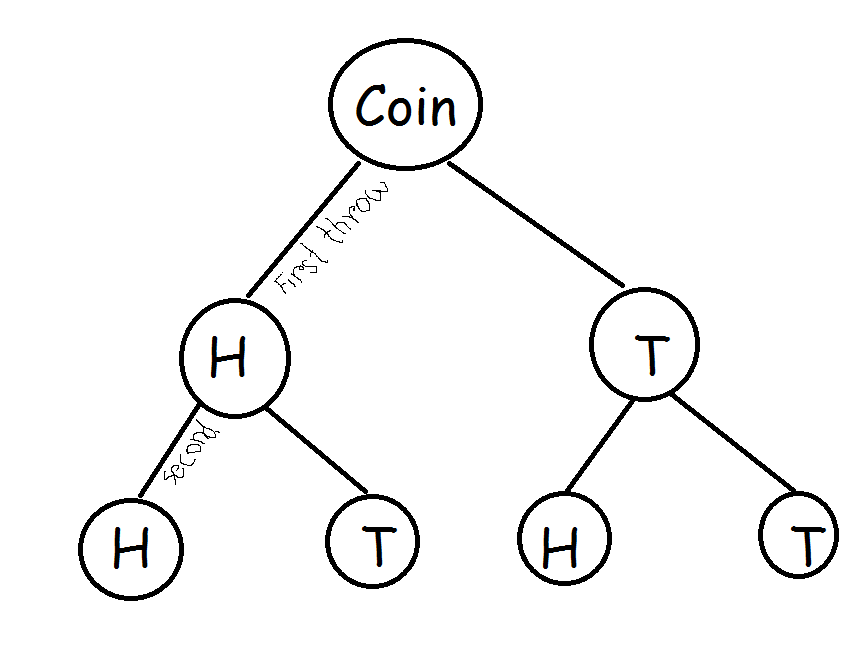
একটি দৈব পরীক্ষায় সম্ভাব্য যা যা ফলাফল আছে, সবগুলো নিয়ে গঠিত সেটকে বলা হয় নমুনাক্ষেত্র। যেমন একটি নিরপেক্ষ মুদ্রা নিক্ষেপের ক্ষেত্রে দুইটা ফলাফল আছে – হেড(H) এবং টেল(T)। তাহলে এই দুইটার সেটই হবে নমুনাক্ষেত্র। অর্থাৎ, নমুনাক্ষেত্র, S = {H, T}
আবার যদি মুদ্রাটি পরপর দুইবার নিক্ষেপ করা হয়, তাহলে ফলাফল আসতে পারে ৪ ধরণের।
তাহলে, এক্ষেত্রে নমুনাখেত্র, S = {HH, HT, TH, TT}
এখানে HH মানে হল, প্রথমবার হেড, দ্বিতীয়বারও হেড। HT মানে হল প্রথমবার হেড, দ্বিতীয়বার টেল। ইত্যাদি…
আবার এই S সেটটির প্রতিটি উপাদান হল একেকটি নমুনা বিন্দু। কেতাবী ভাষায়, নমুনাক্ষেত্রের প্রতিটি বিন্দুকে নমুনা বিন্দু বলে।
এবার দেখা যাক সম্ভবনার সাংখ্যিক মান বের করবো কীভাবে
“Bangladesh has won x% of matches where Shakib has played.” ক্রিকেট খেলা দেখার সময় প্রায়ই এ ধরণের কিছু পরিসংখ্যান ভেসে উঠে। এই কথাটার মাধ্যমে একটা সম্ভাবনা দেখার চেষ্টা করা হয়। যেমন, যেহেতু সাকিবের খেলা x% ম্যাচ বাংলাদেশ জিতেছে, সেহেতু সাকিব যদি আজকে খেলে, তাহলে বাংলাদেশের আজকে জেতার সম্ভাবনা x%। (ধরে নিলাম সব টিম একই মানের খেলা খেলে… অর্থাৎ নিরপেক্ষ ঘটনা!)
তো আমরা এখানে এই সম্ভাব্যতা-টা কীভাবে বের করলাম? আমরা প্রথমেই নিলাম সাকিবের খেলা মোট ম্যাচের সংখ্যা, ধরা যাক ২০০। এরপর নিলাম সাকিবের জেতা ম্যাচের সংখ্যা, ধরা যাক ৮০। বাকিটা ঐকিক নিয়মের খেলা!
২০০ ম্যাচের মধ্যে জিতেছে ৮০ ম্যাচ
অর্থাৎ, ১ ম্যাচের মধ্যে জিতেছে ৮০/২০০ ম্যাচ
খেয়াল কর, এখানে আমরা বের করতে চাই সাকিব খেলা অবস্থায় বাংলাদেশ জেতার সম্ভাবনা। তাহলে,
সাকিবকে সাথে নিয়ে বাংলাদেশ ম্যাচ জেতা হল আমাদের কাঙ্ক্ষিত ঘটনা
সাকিবের খেলা মোট ম্যাচ হল সকল সম্ভাব্য ফলাফল।
আর, সাকিবের জেতা ম্যাচগুলো হল অনুকূল ফলাফল।
এখান থেকে আমরা সম্ভাবতার মূল সূত্রটা দাঁড় করাতে পারি এভাবে, সম্ভাব্যতা = উক্ত ঘটনার অনুকূল ফলাফল/মোট সম্ভাব্য ফলাফল
তাহলে এবার আমরা দেখি আমাদের বের করা সূত্র ঠিক আছে কি না। ধর, তোমাকে বলা হল, একটি নিরপেক্ষ মুদ্রা একবার নিক্ষেপে হেড আসার সম্ভাবনা বের করতে।
তাহলে মোট সম্ভাব্য ফলাফল আছে ২ টি – H আর T
অনুকূল ফলাফল আছে একটি – H
তাহলে সম্ভাবনা দাড়াচ্ছে 1/2 = .5
আবার একইভাবে আমরা টেলের সম্ভাবনা বের করলেও আসবে .5
অর্থাৎ আমাদের সূত্র অনুসারে একটি নিরপেক্ষ মুদ্রা একবার নিক্ষেপে হেড আসার সম্ভাবনা টেল আসার সম্ভাবনার সমান। অর্থাৎ আমাদের সুত্র ঠিক আছে! 😀
আমরা এতক্ষণ বকবক করতে করতে দুই ধরণের সম্ভাবনা দেখে ফেলেছি।
(১) যুক্তিভিত্তিক সম্ভাবনা – যখন হেড আর টেল দুইটা আলাদা ফলাফল বিবেচনা করে সম্ভাবনা বের করলাম
(২) তথ্যভিত্তিক সম্ভাবনা – যখন ম্যাচের পরিসংখ্যান থেকে সম্ভাবনা বের করলাম
তুমি একটা কাজ করে দেখতে পার। তা হল, একটা ১ টাকার কয়েন নিয়ে ২০ বার নিক্ষেপ করতে পার। আমি করে দেখেছি, আমার ১৩ বার এসেছে বঙ্গবন্ধু-র সাইডটা, আর ৭ বার এসেছে শাপলার সাইডটা। অর্থাৎ এক্ষেত্রে, শাপলা সাইড আসার সম্ভাবনা হয়ে গেছে 7/20
আমরা এবার তথ্যের উপর ভিত্তি করে হেড টেলের সম্ভাবনা বের করলাম। কিন্তু আমরা তো বলেছিলাম, দুইটার সম্ভাবনা একই হবে। এক্ষেত্রে হল না কেন? কারণ আমরা পুরোপুরি নিরপেক্ষভাবে কয়েন নিক্ষেপ করতে পারিনি! একবার হয়ত মেরে ছাদের সাথে লাগিয়ে দিয়েছি, আরেকবার হয়ত বাতাস এসে কয়েনটিকে সরিয়ে দিয়েছে, ইত্যাদি! তবে আমরা যদি ২০ বারের বদলে ১০০ বার করতাম, তাহলে রেজাল্টটার মান তত .5-এর আরও কাছাকাছি চলে যাবে। আবার ১০০০ বার করলে আরও কাছাকাছি। অর্থাৎ যত বেশিবার টেস্ট করে দেখবো, আমাদের তথ্যভিত্তিক সম্ভাবনা তত নির্ভুল হবে!
তাহলে এবার কিছু কাজ দেওয়া যাক!
(১) একটি ছক্কা একবার নিক্ষেপে জোড় আসার সম্ভাবনা কত?
হিন্টসঃ জোড় সংখ্যা আছে ৩ টি, মোট ফলাফল আছে ৬ টি
(২) একটি ছক্কা একবার নিক্ষেপে ৪-এর গুণিতক আসার সম্ভাবনা কত?
(৩) একটি মুদ্রা ১০০০ বার নিক্ষেপে ৪৮১ বার টেল পাওয়া গেল। মুদ্রাটি একবার নিক্ষেপে হেড পাওয়ার সম্ভাবনা কত?
(৪) একটি আবাসিক এলাকায় ১৫২ টি পরিবারের মধ্যে ৬১-টি পরিবার প্রথম আলো, ৫৭-টি পরিবার ডেইলি স্টার পড়ে। বাকিরা কোনো পত্রিকা রাখে না, কেউ দুইটা পত্রিকা নেয় না। তাহলে, আমরা যদি হঠাত একজনের বাসায় গিয়ে হাজির হই, তার বাসায় প্রথম আলো পাওয়ার সম্ভাবনা কত? 😀
আরেকটি জিনিস দেখে আজকের মত শেষ করবো। আমরা জানি, সাকিব বাংলাদেশের একজন ক্রিকেটার। এখন যদি কেউ জিজ্ঞেস করে, আজ রাতের ইউসিএল ফাইনালে সাকিবের আবাহনীর হয়ে বার্সেলোনার বিপক্ষে হ্যাটট্রিক করার সম্ভাবনা কত, তাহলে তুমি নিশ্চয় তাকে পাগলই বলবে। কারণ, প্রথমত সাকিব ক্রিকেটার। দ্বিতীয়ত, আবাহনী ইউসিএল খেলে না। তৃতীয়ত, আজ রাতে ইউসিএল ফাইনাল না!
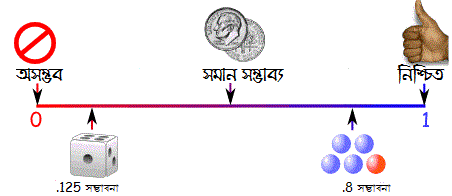
সোজা কথায়, এক্ষেত্রে সাকিবের হ্যাটট্রিক করার সম্ভাবনা শূণ্য(০)। অর্থাৎ এটি হল একটি অসম্ভব ঘটনা।
আবার যদি বলা হয়, আজকে সূর্য পশ্চিম দিকে অস্ত যাওয়ার সম্ভাবনা বের করতে, তাহলে তুমি জান যে সূর্য অবশ্যই পশ্চিম দিকেই অস্ত যাবে। এর অন্যথা হবে না। অর্থাৎ এক্ষেত্রে সম্ভাবনা দাঁড়িয়ে যাচ্ছে ১। অর্থাৎ এটি হল নিশ্চিত ঘটনা।
এখন, এখান থেকে আমরা আরও একটি জিনিস দেখলাম, তা হল কোনো কিছু ঘটার সম্ভাবনা অবশ্যই ০ থেকে ১-এর মধ্যেই থাকবে। ০-এর কম হওয়া সম্ভব না, আবার ১-এর বেশিও হতে পারবে না। তাহলে কোনো একটি দৈব পরীক্ষার পরস্পর বিচ্ছিন্ন ঘটনাগুলোর প্রতিটি পৃথক পৃথক ভাবে ঘটার সম্ভাবনার সমষ্টি ১! 😀 কী? মাথার উপর দিয়ে গেল নাকি? 😀
যেমন ধর, একটি ছক্কার গুটি নিক্ষেপ করা হলে,
১ আসার সম্ভাবনা 1/6
২ আসার সম্ভাবনা 1/6
৩ আসার সম্ভাবনা 1/6
৪ আসার সম্ভাবনা 1/6
৫ আসার সম্ভাবনা 1/6
৬ আসার সম্ভাবনা 1/6
তাহলে সবগুলো ঘটনার সম্ভাব্যতার সমষ্টি = 6 * 1/6 = 1
আজকের মত এখানেই শেষ। 🙂

vaia, tahole majhe moddhe shuni 200% sure, , othoba bivinno company char day 250% eta kivabe?
Let ,total outcome be n and favourable outcome m.
By defination,p(A)=m/n.
Always,m<=n and m non-negative
The value of m can be 0.So,P(A) can be 0.
Again m can be eual to n.P(A) = n/n =1
0<=p(A)<=1
range: 0% ~ 100%
good explanation