হ্যারি পটারের কথা তো সবাই শুনেছি। তো উইজার্ডদের ব্যাংক হল গ্রিনগটস, যার ভল্টগুলো কি না মাটির নিচে। সেখানে এক ভল্ট থেকে আরেক ভল্টে যেতে হয় কার্টে করে, যার দায়িত্বে থাকে একজন গবলিন। এত হাজার হাজার ভল্টের কোনটায় যেতে হলে কোন পথে যেতে হবে, তা তারা মনে রাখে কীভাবে? জাদুকরী শোনায় না ব্যাপারটা? আসলে জাদুর কিছুই না। এসবই ডায়াক্সট্রা বাবাজির খেলা। কীভাবে? আজ কথা বলবো তা নিয়েই।
প্রথমেই আমরা এই সমস্যাটিকে একটি গ্রাফ থিওরির সমস্যায় রূপান্তর করি। আমরা ধরে নিই যে প্রতিটা ভল্ট হল একেকটি নোড। আর যাত্রা শুরু হয় 1 নাম্বার নোড থেকে, যেটি আসলে কোনো ভল্ট না, বরং এটি হল গ্রিনগটসের মেইন হল। তাছাড়া যেহেতু এক ভল্ট থেকে আরেক ভল্টে যাওয়ার দুরত্ব সমান হবে না, তাই আমাদের গ্রাফটি হবে একটি weighted গ্রাফ। তাহলে আমরা নিচের মত একটি গ্রাফ পাবো।
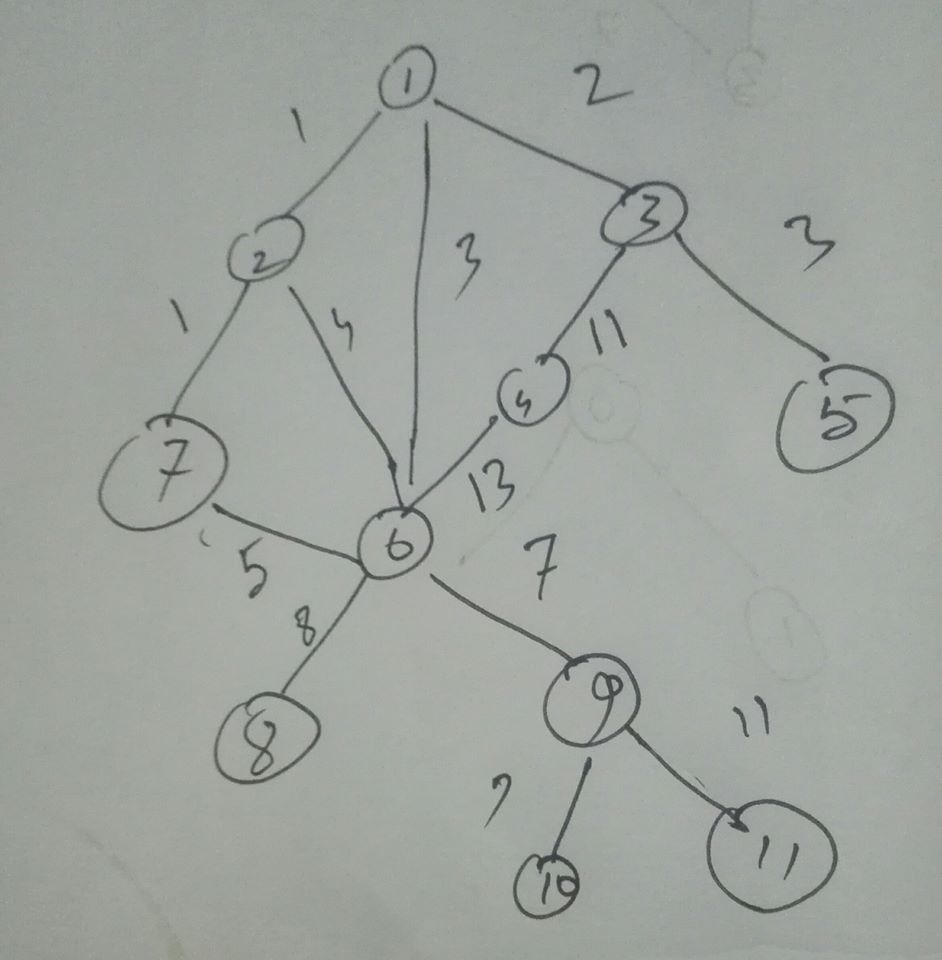
এখন বোঝার ব্যাপার হল, আমরা যদি ১ থেকে ৬-এ যেতে চাই, তাহলে নিশ্চয় সরাসরি ১->৬ এজটা ব্যবহার করবো। কেন? কারণ অন্য কোনো পথে গেলে আমাদের বেশী দুরত্ব যাওয়া লাগবে। তাহলে শুধু ১ নাম্বার নোড থেকে বাকিসব নোডগুলোর সর্বনিম্ন দুরত্ব বের করলেই কাজ শেষ!
এই সমস্যার সাথে কি আমাদের জানা কোনো এলগরিদমের মিল আছে? হ্যা, গ্রাফটি যদি unweighted হত, তাহলে আমরা বিএফএস অথবা ডিএফএস ব্যবহার করেই এই সমস্যা সমাধান করে ফেলতে পারতাম। কিন্তু এখন ঝামেলা হল গ্রাফটি weighted. দেখেই বোঝা যাচ্ছে সরাসরি বিএফএস এখানে কাজ করবে না। ১->৬ এজটার কস্ট যদি ১০০ হত, তাহলে বিএফএস বলতো যে এটাই সর্বনিম্ন দুরত্ব, যদিও এর চেয়ে কম দুরত্ব দিয়ে ১ থেকে ৬-এ যাওয়া যায়। তাহলে কী করা যায়? আমরা প্রথমেই বিএফএসকে একটু একটু করে পরিবর্তন করার চেষ্টা করি।
ধরা যাক, আমাদের কাছে নিচের গ্রাফটি আছে।
আমরা প্রথমে বলবো যে, প্রতিটি নোডের দুরত্ব INF (এটা প্রবলেম অনুসারে ঠিক করতে হবে, এমন কোনো বড় মান, যেটা কোনোভাবেই ঘটা সম্ভব না। অথবা -1 দিয়েও ইনিশিয়ালাইজ করা যায়। কিন্তু সেক্ষেত্রে আলাদা ভাবে চেক করে নিতে হয়)। এরপর আমরা বলি যে (১ থেকে) ১-এর দুরত্ব ০। এরপর আমরা নিচের মত একটি এলগরিদম নিয়ে কাজ করি।
int distance[MAX];
for (int i=0; i<MAX; i++) distance[i] = INF;
queue <int> Q;
Q.push(1);
while (!Q.empty) {
int currentNode = Q.front();
Q.pop();
for (int i=0; i<edge[currentNode].size(); i++) {
if (distance[edge[currentNode][i]] == MAX) {
distance[edge[currentNode][i]] = distance[currentNode] +
cost[currentNode][i];
}
}
}
৬ নাম্বার লাইনে আমরা কিউ-তে যে নোড প্রথমে আছি, তাকে নিচ্ছি। এরপর এই নোডের সাথে সংযুক্ত সব নোডের দুরত্ব আপডেট করে নিচ্ছি। তাহলে আমরা নিচের মত দুরত্ব পাবো।
খেয়াল কর, যেহেতু আমরা বিএফএসের মত করে করেছি, তাই প্রতিটি নোডে খুব বেশীতে একবার যাওয়া যাবে। তাই আমরা যখন ৪ নাম্বার নোড কে (২ থেকে) একবার ভিজিট করে ফেলেছি, এরপর আর ৩ থেকে এই নোডে আসতে পারি নাই। একারণে ৩->৪ (নীল কালিতে চিহ্নিত) এই এজটা অব্যবহৃত থেকে গেছে।
কিন্তু খেয়াল কর, যদি আমরা এই এজটা ব্যবহার করতাম, তাহলে ৪ নাম্বার নোডটার দুরত্ব কমে হত ৪+২ = ৬, যার কারণে আবার এর সাবট্রীতে যত নোড আছে সবগুলোর দুরত্বই কমে যেত। যে নোডগুলোর দুরত্ব এভাবে কমা সম্ভব, কিন্তু আমাদের এলগরিদমে কমানো যায় নি, সেগুলো সবুজ রঙে চিহ্নিত।
আমরা ব্যর্থ হলাম প্রথম চেষ্টায়। তবে হতাশ হওয়ার কিছুই নেই, আমরা সমাধানের দিকেই আগাচ্ছি। :p এখন তাহলে আমাদের এলগরিদমে আরো একটু পরিবর্তন আনা দরকার। আমরা এখন যা করবো তা হল, আমরা যখন দেখবো কোনো নোডের সাথে সংযুক্ত একটি নোড আগে ভিজিট করা হয়েছে, তখন আমরা চেক করে দেখবো এই এজটা ব্যবহার করলে ওই নোডের দুরত্ব কমে কিনা। এটি একটা (distance[edge[currentNode][i]] > distance[currentNode] + cost[currentNode][i]) চেক দিয়েই করে ফেলা সম্ভব।
ধরা যাক, এভাবে আপডেট করলাম। কিন্তু এর সাবট্রীতে যেসব নোড আছে, তাদের কী হবে? তাদের কাজ করতে চাইলে আমাকে এই নোডটিকে কিউ-তে পুশ করে দিতে হবে। তারপর যখন এই নোডের সুযোগ আসবে, তখন এর সাবট্রীও আপডেট হয়ে যাবে। তাহলে আমাদের বর্তমান এলগরিদম দেখতে এরকমঃ
int dis[MAX];
for (int i=0; i<MAX; i++) dis[i] = INF;
queue <int> Q;
Q.push(1);
while (!Q.empty) {
int cur = Q.front();
Q.pop();
for (int i=0; i<edge[cur].size(); i++) {
if (dis[edge[cur][i]] > dis[cur] + cost[cur][i]) {
dis[edge[cur][i]] = dis[cur] + cost[cur][i];
Q.push(edge[cur][i]);
}
}
}
অভিনন্দন, আমরা প্রায় গন্তব্যে পৌছে গিয়েছি। আমাদের এখন কেবল ছোট্ট একটা পরিবর্তন করা দরকার। তাহলেই আমরা গ্রিনগটসের (এবং ডায়াক্সট্রা) সব রহস্য জেনে যাবো! 😉
খেয়াল করো, আমরা এখানে একটি সাধারণ কিউ ব্যবহার করেছি, যেটা কিনা আগে আসলে আগে পাবেন ভিত্তিতে কাজ করে। আমরা যখনই কোনো একটি নোডকে এই কিউতে রাখি, এটা নোডটাকে সবার শেষে রেখে দেয়। এরপর নোডটাকে অপেক্ষা করতে হয়, যতক্ষণ না তার আগের সব নোডের কাজ শেষ হয়। আমরা এখানে নোডটার দুরত্ব কত, তা নিয়ে কোনো মাথা ঘামাচ্ছি না। এটা কি ঠিক হচ্ছে? যেসব নোড রুট থেকে কাছে, তাদেরকে নিয়েই কি আগে কাজ করা উচিত না?
তাই আমরা এখানে একটি min priority_queue ব্যবহার করবো, যেটা আমাদেরকে কিউ থেকে সবচেয়ে কম দুরত্বের নোডটি খুজে পেতে সাহায্য করবে। আর আমাদের এলগরিদমের কমপ্লেক্সিটি হবে O(V log V + E log V)।
struct element{
int node, path_cost;
element(){}
element(int _node, int _path_cost){
node = _node;
path_cost = _path_cost;
}
// The following is to ensure a min priority queue
bool operator >(const element &a)const {
return path_cost > a.path_cost;
}
} ele;
void dijkstra (int root) {
for (int i=0;i<MAX; i++) dis[i] = INF;
dis[root] = 0;
priority_queue <element> q;
q.push(element(root, 0));
while (!q.empty()) {
element nxt = q.top();
q.pop();
int nx = nxt.node;
for (int i=0; i<edge[nx].size(); i++) {
element tmp;
tmp = element(edge[nx][i], cost[nx][i]);
if (dis[tmp.node] > dis[nx] + cost[nx][i]) {
dis[tmp.node] = dis[nx] + cost[nx][i];
q.push(element(tmp.node, dis[tmp.node]));
}
}
}
}
এখানে মূলত যে দুইটা ধারণা ব্যবহার করা হয়েছে, তা হলঃ
- প্রায়োরিটি কিউঃ এটি মূলত একটি min heap। এখান থেকে সবচেয়ে কম দুরত্বের নোডটা বের করে নেওয়া যায়। এবং এটি ব্যবহার করার কারণ হল এটি কাজ করে O(log n)-এ। যেখানে সাধারণ লুপ চালিয়ে করলে লাগতো O(n)। প্রায়োরিটি কিউ ব্যবহার করার কারণ ব্যাখ্যা করি নাই। তবে মোটামুটি একটা বড় গ্রাফ নিয়ে হাতে কাজ করলেই বুঝতে পারবে যে, কিউ ব্যবহার করলে যতবার আপডেট করতে হচ্ছে, প্রায়োরিটি কিউ ব্যবহার করলে তার চেয়ে অনেক কম আপডেটেই কাজ হয়ে যাবে।
- পাথ রিলাক্সেশন (Path Relaxation): যখন কোনো একটি এজ ব্যবহারের কারণে কোনো নোডের দুরত্ব কমে, আমরা শুধু তখনই ওই এজটি ব্যবহার করছি। এ ধারণাকে বলা হয় পাথ রিলাক্সেশন।
তো, আমি তো অনেক ভাব নিলাম গবলিনদের সাথে। আমি তাদের সব রহস্য জেনে গেছি। তখন তারা রেগে গিয়ে আমাকে একটা ভল্টে রেখে দিয়ে চলে গেল। এবার আমি ফিরে যাবো কীভাবে? আমি তো আগেই গ্রাফ বানিয়ে রেখেছি, কিন্তু সেই হিজিবিজি থেকে এখন আমার পথটা খুজে পাবো কীভাবে?
এখন আমার সমস্যা হল, একটা গ্রাফ এবং একটা রুট দেওয়া থাকলে কীভাবে সেই রুট থেকে বাকি সব নোডে যাওয়ার পথ বাতলে দেওয়া যায়, যাতে দুরত্ব সর্বনিম্ন হয়। আমরা কি এই এলগরিদমের সাথে আর কিছু অতিরিক্ত ইনফর্মেশন ব্যবহার করেই এই সমস্যাটা সলভ করতে পারি? সেটা চিন্তা কর। আশা করি পারবে, না পারলে কমেন্টে জানিও।
ডায়াক্সট্রা কখন ব্যবহার করবো এবং কখন করবো না?
আমরা ডায়াক্সট্রা তখনই ব্যবহার করতে পারবো, যখন গ্রাফে কোনো নেগেটিভ সাইকেল থাকবে না। নেগেটিভ সাইকেল মানে কী? নেগেটিভ সাইকেল মানে হল এমন একটা সাইকেল, যার টোটাল কস্ট ০-এর চেয়ে কম। নেগেটিভ সাইকেলের ক্ষেত্রে কীভাবে সর্বনিম্ন দুরত্ব বের করতে হয়, তার জন্য জানতে হবে বেলম্যান ফোর্ড। সেই বেলম্যান ফোর্ড নিয়ে আলোচিত হবে আগামী পর্বে!
ডায়াক্সট্রা ব্যবহার করে সলভ করা যায় এমন কিছু সমস্যা
হঠাত কেন ডায়াক্সট্রা লিখলাম
আসলে লেখার মটিভেশন হারিয়ে ফেলেছি। তাই লেখা হয় না সচরাচর। আজ সকালে হঠাত Quora-তে একটা প্রশ্ন দেখছিলাম। সেটার উত্তর দেওয়ার পর ভাবলাম উত্তরটা এখানেও লিখে ফেলি। তাই লেখা। মটিভেশন আবার উধাও না হলে আশা করি বাকিগুলো নিয়েও লিখবো। হ্যাপি কোডিং!

vai, last e je problem tar kotha bollen ota bujhi nai,, apni 1 ke root dhorei sob node e jawae shortest path gula ber kortesen na?
Not the “shortest path” , but the “Second best shortest path”.