সাইকেল খুজে বের করা – ফ্লয়েডের খরগোস এবং কচ্ছপ এলগরিদম

আমরা বাস্তব জীবনে অনেক সময়ই এমন ফাংশন দেখি, যেগুলোতে কিছুদূর পর পর একই মান পুনরাবৃত্তি হতে থাকে। কথা না বাড়িয়ে একটি উদাহারণ দিয়ে ফেলি। ধরা যাক, আমাদের কাছে একটি ফাংশন আছে এমনঃ

f(x) = (f(x-1) * 2) % 10, for n > 0।

এখানে % হল মডুলাস অপারেশন।

আর ফাংশনের বেস কেস হল f(0) = 1

এখন বলা হল, f(1000000000)-এর মান বের করতে। কীভাবে করা যায়? একটি উপায় হল লুপ চালিয়ে দেওয়া।

#include <bits/stdc++.h>
using namespace std;
int main () {
    int n;
    scanf("%d", &n);
    int cur = 1;
    for (int i=1; i<=n; i++) {
        cur = cur * 2;
        cur = cur % 10;
    }
    printf("%d\n", cur);
    return 0;
}

কিন্তু বুঝতেই পারছো এটি প্রচন্ড ইনএফিসিয়েন্ট। আমরা অন্য কোনো উপায় বের করার চেষ্টা করি।  আমরা ফাংশনটির প্রথম কিছু এলিমেন্টের মান বের করে ফেলি।

f(0)	1
f(1)	2
f(2)	4
f(3)	8
f(4)	6
f(5)	2
f(6)	4
f(7)	8
f(8)	6
f(9)	2

এখানে খেয়াল কর, f(5)-এ গিয়ে f(1)-এর মান পুনরাবৃত্তি হয়েছে, এবং এই মান এর পর আবার f(9)-এ গিয়ে আবার এসেছে। এবং মাঝের এলিমেন্টগুলো একই (2, 4, 8, 6)। তাহলে বুঝতেই পারছো, এখন f(1000000000) বের করা আর কোনো ব্যাপারই না! যেকোনো n>0-এর জন্য আমরা এখন লিখতে পারিঃ

if (n%4 == 0) f(n) = f(4);
else f(n) = f(n%4);

কিন্তু সমস্যা হল সবসময় আমাদের এত সহজ ফাংশন দেওয়া হবে না। এবং আমরাও এত সহজে সাইকেল (চক্র)টা খুজে বের করতে পারবো না। যেমনঃ ফাংশনটি হতে পারে এমনঃ

f(x) = (2f(x-1) + 3f(x-2))  % 1000, for n > 1

f(0) = 0, f(1) = 1

এধরণের ক্ষেত্রে আর কাজটা এত সহজ থাকবে না! কিন্তু খেয়াল করো, আমাদের এ ধরণের সমস্যা সমাধানের জন্য কেবল দুইটা প্যারামিটার জানা দরকার।

• সাইকেলটা কোথায় শুরু হয় (miu)
• সাইকেলটার দৈর্ঘ কত (lambda)

আমরা ফ্লয়েডের (Hare and Tortoise Algorithm) এলগরিদম দিয়ে এই কাজটি সহজেই O(n)-এ করতে পারি।

আমরা প্রথমে একটি খরগোস (hare) আর কচ্ছপ (tortoise) নিবো। এদেরকে আমরা শুরুতে রাখবো f(0)-তে। এবার খরগোস প্রতি ধাপে দুই ঘর করে আগাবে। আর কচ্ছপ আগাবে এক ঘর করে।  যেহেতু এই ফাংশনে সাইকেল আছে, তাহলে কোনো এক সময়ে খরগোস এবং কচ্ছপ অবশ্যই একে অন্যের দেখা পাবে।

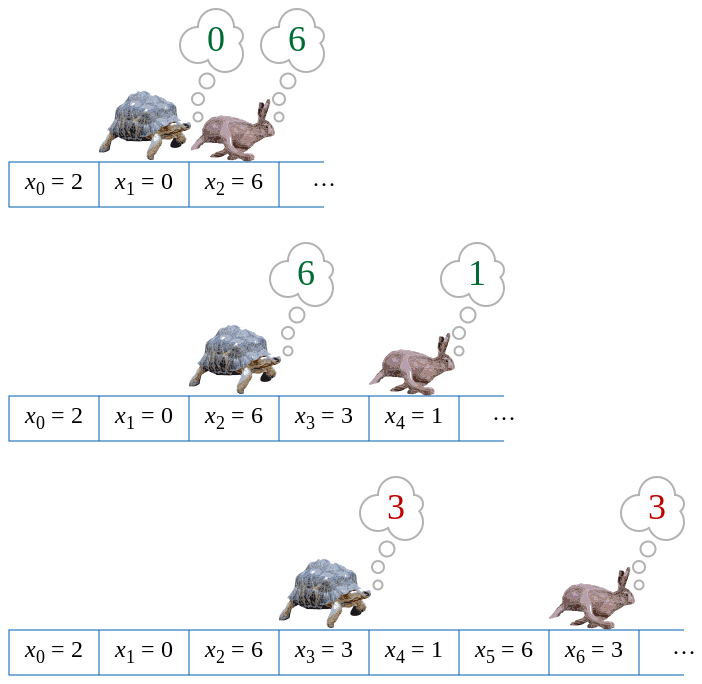আমাদের সাইকেলটি দেখতে হবে এমনঃ

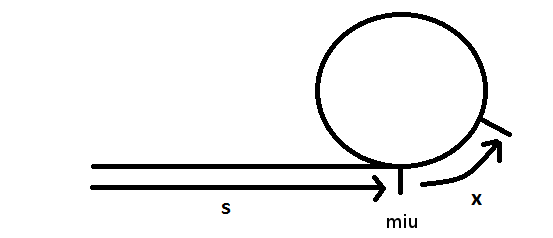
ধরা যাক, তাদের s+x বিন্দুতে দেখা হল। এখন এ সময় কচ্ছপ যদি s+x  দুরত্ব অতিক্রম করে, তাহলে খরগোস অতিক্রম করেছে 2(s+x) দুরত্ব। কারণ, কচ্ছপ যে দুরত্ব যায়, খরগোস যায় তার দ্বিগুণ। অর্থাৎ, খরগোস অতিরিক্ত s+x দুরত্ব অতিক্রম করে আগের জায়গায় ফিরে এসেছে। তাহলে আমরা এটাও বলতে পারি যে, সে (খরগোশ) যদি এর চেয়ে x দুরত্ব কম অতিক্রম করতো, তাহলে সে থাকতো সাইকেল শুরুর বিন্দুটিতে (miu)। কারণ কচ্ছপ miu-থেকে x দুরত্ব বেশী এসেই খরগোসের সাথে মিলিত হয়েছিল। সাথে আমরা এও বলতে পারি যে, s+x থেকে আরো s দুরত্ব গেলে miu বিন্দুতে ফিরে আসা যায়।

এখন আমরা খরগোসটিকে ধরে আবার f(0) তে নিয়ে যাই, এবং কচ্ছপটিকে s+x-এই রেখে দিই। এখন যদি দুই জনকেই একই গতিতে আগাতে থাকি, তাহলে তারা একে অপরের দেখা পাবে s দুরত্বে এসে। তাহলে এভাবে আমরা সহজেই সাইকেল কোথায় শুরু হয়েছে, তা বের করে ফেলতে পারি।

আর সাইকেলের দৈর্ঘ্য বের করার জন্য আমাদের s+x বের করতে হবে। আমরা আগেই দেখেছি, s+x থেকে যদি আবার যাত্রা শুরু করাই, তাহলে কিছু স্টেপ পরে সে আবার একই জায়গায় ফিরে আসে। তাহলে আমরা কচ্ছপকে s+x বিন্দু থেকে হাটিয়ে দিবো। সে যখন আবার এই বিন্দুতে ফিরে আসবে, তখন বুঝবো যে আমরা সাইকেলের দৈর্ঘ্য পেয়ে গিয়েছি।

তাহলে এলগরিদমটা দাড়াচ্ছে এমনঃ

১। প্রথমে খরগোস এবং কচ্ছপকে f(0)-তে রাখবো। খরগোস আগাবে দুই ধাপ করে, আর কচ্ছপ আগাবে এক ধাপ করে।

২। এভাবে একসময় তারা দেখা করবে, অর্থাৎ ফাংশনের মান একই হবে। এবার কচ্ছপকে থামিয়ে রেখে খরগোসকে এক ধাপ করে আগাতে থাকলে খরগোস যখন আবার lambda স্টেপ পর ওই বিন্দুতে ফিরে আসবে। এভাবে আমরা দৈর্ঘ্য পাবো।

৩। এবার কচ্ছপকে ওই বিন্দুতে রেখে, আর খরগোসকে f(0) তে নিয়ে গিয়ে দুই জনকেই এক ধাপ করে আগাতে থাকলে তারা যে বিন্তুতে মিলিত হবে, সেটা হবে miu।

আশা করি কোড করে ফেলতে পারবে। 🙂

 

প্রবলেম লিংক – Sequence Analysis। আমার কোডটি আছে এখানে। কোডে প্রায় সবই কমেন্টে বলা আছে। আশা করি বুঝতে কোনো সমস্যা হবে না।