আসসালামুয়ালাইকুম।
একটা নিজস্ব অভিজ্ঞতা দিয়েই শুরু করি লিখিত বকবকানির প্রথম অংশটা।
প্রথম যখন লগারিদম জিনিসটার হাতে খড়ি হয় স্কুল জীবনে,
তখন ছোট্ট স্কুলজীবনের অনুভুতি দিয়ে আঁচ করলাম দশ ভিত্তির লগারিদমের উপরে কিছুই হয়না। :v
বিশাল বিশাল সংখ্যার ডিজিটসংখ্যা বের করা,(যেমন 55365),গনণার কাজ গুলো সুবিধার সাথে করা,বিচ্ছিরি বিচ্ছিরি হিসাবগুলো সহজে লগারিদম চার্ট ব্যবহার করে করা। 😀
সংখ্যার power নিয়ে ছেলেখেলা করা।
কি না হয় এ দিয়ে!! 😀
কিন্তু তারপরও আমাদের পাঠ্যবই এ আরেকধরনের লগারিদম দেখানো ছিল।
সেই লগারিদমের ভিত্তি হিসেবে একটা ছোট্ট ধ্রুবকের সাথে পরিচয় করিয়ে দেওয়া হয়েছিল।
e=2.718281828………
(পরে জেনেছি সারা বিশ্বে এটা অয়লার ধ্রুবক নামে খ্যাত)
এবং বই এ লেখা ছিল এধরনের লগারিদমকে ন্যাচারাল লগারিদম বলা হয়।
বিন্দুমাত্র বুঝিনি এই লগারিদমের দরকারটা কি যেখানে দশ ভিত্তি আছেই।
তার উপরে লগারিদম আবার ন্যাচারাল হয় কেমনে!!
অনেক ভাবিয়েছিল প্রশ্নটা।উত্তর তখনই পাই নি অবশ্য!!
যারা ইতোমধ্যে ক্যালকুলাসের মহাসমুদ্রের কয়েক মুষ্ঠি জল ইন্টারমেডিয়েট সিলেবাসের মধ্যে দিয়ে নিতে শুরু করেছো তারাও জানো যে ক্যালকুলাসের প্রতি পদে পদে e এর ব্যবহার।
এমনকি ফিজিক্স এবং ক্যামিস্ট্রিতেও এর ব্যাপক ব্যবহার।
এই অয়লার ধ্রুবক জিনিসটা আসলে কি এবং কি ইবা এত প্রাকৃতিকতা এই ধ্রুবকের,সব ধাপে ধাপে বুঝার চেষ্টা করি চল।
শুরুতেই বলে দিচ্ছি আমি হয়ত অয়লার ধ্রুবকের বিশাল সম্রাজ্যের সর্বত্র বিচরণ করতে পারব না,তবে তোমাদের ব্যাপারটা অনুভব করানোর যথাসাধ্য চেষ্টা করব। 🙂
আমি এই লেখায় যথাসম্ভব চেষ্টা করব ক্যালকুলাস কিংবা ইন্টারমেডিয়েট ম্যাথমেটিকস এড়িয়ে চলার।
তারপর দুএক জায়গায় এসবের প্রয়োজন হয়ত হবে এবং তা যথেষ্ঠ সহজবোধ্য ভাবে উপস্থাপনের চেষ্টা করব ইনশাল্লাহ।
উদাহরণগুলো একটু হাতে কলমে খাতায় করে দেখাটা প্রয়োজন।
😀
ক্যালকুলাস জগৎ এ যারা ইতোমধ্যে প্রবেশ করেছো বা করতে শুরু করেছো,তারা নিশ্চয় জানো যে ক্যালকুলাসের একটা বিশাল শাখা কাজ করে বৃদ্ধির হার বা rate of growth নিয়ে।(না জানলেও সমস্যা নেই।)
এবং মজার ব্যাপার হল প্রকৃতির প্রায় সকল “rate of growth” এ e জিনিসটার ছোয়া আছে।
সেটা বায়োলোজির ব্যাক্টেরিয়ার বৃদ্ধির হার থেকে শুরু করে অর্থনীতির ব্যাংক এ চক্রবৃদ্ধিসুদের হার।
এমনকি ক্যামিস্ট্রির সক্রিয়ন শক্তিপ্রাপ্ত অনুর সংখ্যা থেকে ফিজিক্সের তেজস্ক্রিয়তা পর্যন্ত অনেক কিছুতেই।
(সাব্জেক্ট ভেদে বল্লাম,e এর depth বুঝাতে 😛 )
এমনকি তোমার শরীরের কোষের মৃত্যুর হারে পর্যন্ত আছে এই e। 🙂
টর্নেডো,শামুকের আকৃতি,এমনকি “মোনালিসা” ছবিটায় ও আছে এর প্রভাব।
সৃষ্টির আদিকাল থেকে প্রকৃতি ও e “in a relationship” বলতে পার। 😛
e সংখ্যাটা π এর কাজিন বলে ধরে নিতে পার প্রাথমিকভাবে। 😀
দুই কাজিনেরই চোখে পড়ার মত যে মিলটা সেটা হচ্ছে দুটোই অমূলদ সংখ্যা।
যদিও π জিনিসটা যত সহজে অনুভব করা যায় e এত সহজে ধরা দেয় না।
এদের মধ্যে নানানভাবে সম্পর্ক রয়েছে।
এই লেখার শেষে আমরা পৃথিবীর সব থেকে সুন্দর equationটা দেখব,যেখানে π আর e এর সরাসরি একটা সম্পর্ক থাকবে।
আপাতত তোলা থাকুক সেটা।
e এর সংজ্ঞা হিসেবে “rate of change” বলা কিংবা ম্যাকলরিনের ধারা দিয়ে আসা সিরিজের সাহায্যে মান বের করাটা বেশ প্রচলিত আছে।
তেষ্টা মেটেনা বলে আমি এর ধার দিয়েও যাব না। 😛
তবে ম্যাকলরিনের e এর মানের সিরিজটা আগ্রহীরা চাইলেই দেখে নিতে পার নিজেদের পাঠ্যবই এ কিংবা গুগলে।
তবে চলো এবার e জিনিসটাকে গতবাধা জগতের খানিক বাইরে গিয়ে অনুভব করার চেষ্টা আমরা করি। 🙂
আমার মনে হয় শুরুতেই তোমাকে e নিয়ে একটু চমকে দিতে পারলে ভাল হয়। 😀
চলো একটা সহজ জিনিস করি।
১০ সংখ্যাটাকে আমরা কয়েকটা সমান ভাগে ভাগ করব।তারপর তাদের পরস্পর গুণ করব।
প্রথমে ধর ১০ কে ২টুকরো করে গুণ করলাম।তখন আসে
5×5=25
এবার ১০ কে ৮টুকরা করলাম।
তাহলে আসে
(10÷8)8 = 5.960464478
কিংবা ১০ টুকরাই করি
তখন গুণফল
110=1
চেষ্টা করে দেখ তো জিনিসটা,
গুণফলটা সর্বোচ্চ কখন হচ্ছে??একটু খাতা কলম নিয়ে বসে করেই দেখ নাহয়।
বললে হয়ত অবাক হবে যে কাটা টুকরাগুলার মান যদি e এর খুব কাছের হয় তাইলে গুণফল সর্বোচ্চ হবে!!
বিশ্বাস হলো না!?
তাইলে এখন ধরি 2.5 করে হবে প্রতি টুকরা(e এর কাছাকাছি ভ্যালু।আপাতত মেনে নাউ। :3 )
মানে চারভাগ করা যাবে বরাবর।(10÷2.5 =4)
(2.5)4 = 39.0625
৪ ভাগ থেকে বেশি ভাগে কেটে কিংবা কমভাগে কেটেও গুণফল এত বেশি আসে নি 😀
এখন দেখি জিনিসটা যদি একদম বরাবর e বসাই তাহলে কেমন আসে।
(ভয় পেয়োনা। 😛 ক্যালকুলেটরে করে দেখ নীচের মত)
প্রতি পিস e এর সমান করে কাটলে 10÷e খানা পিস হয়।
তাহলে।
e(10÷e)=39.59862564….
এটাই সর্বোচ্চ গুণফল!!
আমি “পেয়াজকলি প্রকাশনির” বই এর মত লাখটাকার বাজি ধরে বলতে পারি যে এর চাইতে বেশি গুণফল উপরের শর্ত মেনে বের করে দেখাতে পারবেনা। 😛
শুধু ১০ বলে নয়,যেকোন সংখ্যার ক্ষেত্রে এটা সত্য!!চেষ্টা করেই দেখ নাহয়!
চল এবার মূল আলোচনায় যাওয়া যাক।এই চমকটা উঠানো থাকুক আপাতত।
e কে অনুভুতি দিয়ে বোঝার ব্যাপারটাতে আসি।
শুরুর কথাগুলো অনেক অন্য উদাহরণ দিয়েই শুরু করা যেত।
তবে মুনাফা আর মূলধনের ব্যাপার দিয়ে শুরু করাটা বেশ practical বলে মনে হলো।
চক্রবৃদ্ধি মুনাফার ব্যাপারটা অনেকেই জানো।স্কুল লেভেলের ভয়ঙ্কর শ্বাসরোধী একটা টপিক :v
জিনিসটা একটু ভেতর থেকে explain করেই বলি।
ব্যাংকে রাখা টাকার উপর নির্দিষ্ট পার্সেন্টেজে মুনাফা দেওয়া হয় এটা সবাই জানো।
ধর,আমি ব্যাংকে 100 টাকা রাখব।
ব্যাংক আমাকে 5% হারে সরল মুনাফা দেবে প্রতি বছর।
তাইলে প্রথম বছর আমার টাকা হবে 105
দ্বিতীয় বছর 110 তৃতীয় বছর 115 এভাবে চলতে থাকবে।
কিন্তু চক্রবৃদ্ধি মুনাফার ক্ষেত্রে প্রতিবার মুনাফা দেওয়ার পর মুনাফা সহ মোট টাকার(সুদাসল যেটাকে বলে) উপর আবার মুনাফা apply হবে।
100 টাকা রাখার এক বছর পর যখন 105 টাকা হবে
এই সুদাসলের উপর পরবর্তী মুনাফা প্রয়োগ হবে।
প্রথমবার r হারে(% এ) মুনাফা প্রয়োগে মুলধন বেড়ে হবে
P(1+r)
এখানে P=আদিমূলধন,r=বার্ষিক মুনাফার হার,
এইটা এবার মূলধন হিসেবে কাজ করবে।
এবার আরেকবার সুদ প্রয়োগ হলে সুদাসল হবে,
P(1+r)2
জিনিসটাকে গাণিতিকভাবে t বার সুদ প্রয়োগের জন্য লিখলে
চক্রবৃদ্ধি সুদাসলP’=P(1+r)t
( সরল মুনাফা থেকে বেশি লাভজনক।ব্যাংকে টাকা রাখার সময় মাথায় রাখতে পার। 😉 :-P)
এখন একটা নতুন তথ্য দি তোমাদের।
অনেক ব্যাংক নানান রকম চুক্তি করে।ধর তারা বলল যে তোমাকে 5% মুনাফাই দেবে প্রতি বছরে।তবে তা তোমাকে দিতে পারে বছরে 12 ভাগ করে কিংবা 52 ভাগ করে কিংবা এমনকি প্রতি দিন হিসেবে।মানে 365 ভাগ করে।
তাহলে আমাদের সূত্রটাকে একটু অন্যভাবে লেখা যাক।
P’=P(1+r/n)(nt)
(এখানে t এর জায়গায় nt হচ্ছে কারণ t বছরে n বার করে মুনাফা apply হচ্ছে।মোট nt বার।
আর প্রতিবার মুনাফা r/n হারে দেওয়া হবে)
চার্টটা দেখ।
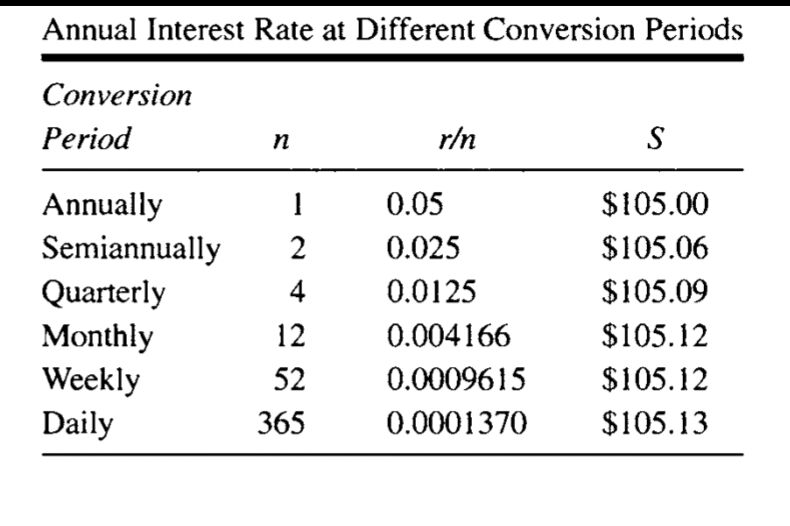
মনে হচ্ছে যেন n এর মান বাড়াব আর টাকার পরিমাণ বাড়তেই থাকবে!
(ব্যাংককে বলে ব্যবস্থা করতে দেখতে পার ^_^ )
এখন আমি তোমাদেরকে আরো একটা হিসেবের চার্ট দেখাব,এই চক্রবৃদ্ধিসুদাসল এর সূত্র ব্যবহার করে।
হিসেবের জটিলতা না আনার জন্য ধরে নেব আমার মূলধন,P=1টাকা
(গরিব মানুষ।মূলধন একটাকা হতেই পারে)
এবং 100% হারে মুনাফা দেওয়া হচ্ছে (যদিও কোন ব্যাংক কখনো দেয়না।কিপ্টা সব -_- )
অর্থ্যাৎ
r=100%=1
আর হিসেবটা আমরা এক বছরের জন্য করব মানে
t=1
অর্থ্যাৎ
P’=(1+1/n)n
আমরা n এর একেক মানের জন্য হিসেবটা কেমন হয় দেখব।

প্রথমে মনে হয়েছিল না কেবল n এর মান বাড়িয়ে বড়লোক হয়ে যাওয়া সম্ভব?? 😛
n এর ক্রমশ মান বাড়তে বাড়তে হতাশাও বাড়ল।
কারণ এটা একটা নির্দিষ্ট সংখ্যার দিকে অগ্রসর হচ্ছে।
সংখ্যাটা=2.718281828….
বিশ্বাস না হলেও এটাই হচ্ছে সেই বিখ্যাত অয়লার ধ্রুবক e 😀
প্রমাণ চাইলে ক্যালকুলেটর চেপে মিলিয়ে দেখো। 😀
এখন প্রশ্ন হল আমি হিসেবের সুবিধার জন্য p,t,r সবের মান 1 ধরে নিয়েছি।
এগুলোর অন্য মানের জন্য তো ফলাফল e নাও আসতে পারে।
ঠিক ধরেছো e আসবে না সবক্ষেত্রে।
কিন্তু n.ex জাতীয় কিছু আসবে।যেখানে n,x বাস্তব সংখ্যা।
তাও e এর প্রভাব থেকেই যাবে।
এখন নিশ্চয় অনেকে প্রশ্ন করে উঠবে ভাইয়া সবই বুঝলাম।ব্যাংকের সাথেই বা প্রকৃতির সম্পর্ক কি!?
আপনি বলেছিলেন e এর সাথে প্রকৃতির সম্পর্ক অনেক গাঢ়।
আপনি তো ব্যাংকের সম্পর্ক গাঢ় করে দিলেন e এর সাথে। :'(
(সুনীল গঙ্গোপাধ্যায় এর কবিতার মত করে বলতেই পার “কেউ কথা রাখেনি” 😛 )
এখানে আসল বোঝার জিনিসটা ব্যাংক বা চক্রবৃদ্ধি মুনাফা নয়।
জিনিসটা বোঝো প্রতিবারের মুনাফা মুলধনে add হচ্ছে।
প্রকৃতিও কি এমন নয়??
ব্যাক্টেরয়ার ক্ষেত্রেই ধর।
১০০ ব্যাক্টেরিয়া প্রতি সেকেন্ড এ জন্ম দিল আরো ৫ টা ব্যাক্টেরিয়ার।(যদিও জন্ম জিনিসটা ব্যাক্টেরিয়ার ক্ষেত্রে বলাটা উচিত না। :-P)
এই ৫টা ব্যাক্টেরিয়া সহ ১০৫ টা ব্যাক্টেরিয়া একসাথে পরের প্রজন্ম জন্ম দিবে পরে।
এবং ব্যাক্টেরিয়ার ক্ষেত্রেও উপরের চার্টটার analogy আনা যেতে পারে।
তাহলে ব্যাংকের টাকা,ব্যাক্টেরিয়া….
হচ্ছেটাকি আসলে???
সুন্দরভাবে এক কথায় বলতে গেলে
এদের প্রত্যেকের ক্ষেত্রে
“বৃদ্ধির হার উপস্থিত সংখ্যার সমানুপাতিক”
মানে উপস্থিত সংখ্যা বাড়লে বৃদ্ধির হারও বাড়বে।
কমলে কমবে।
এটা পরমাণুর ক্ষেত্রে হোক (তেজস্ক্রিয়তায়)
অনুর সংঘর্ষের ক্ষেত্রে হোক।(রসায়নের সংঘর্ষ তত্ত্বে)
কিংবা হোক অন্যান্য যেকোন কিছুর ক্ষেত্রে।
জিনিসটা বুঝলে না??
ব্যাক্টেরিয়া বেশি থাকলে জন্মাবেও বেশি কম থাকলে কম।
যেমন তোমার টাকা বেশি থাকলে দান খয়রাতও বেশি হবে।গরীব মিস্কিন বন্ধুদের ট্রিট বেশি দেবে! 😛
টাকাপয়সা কমে গেলে দান খয়রাতও কমে যাবে। 😀
এটা কেবল মজা করার জন্য বলা।
কিন্তু তুমি একটু ভাল করে প্রকৃতিতে তাকিয়ে দেখলে এরকম জিনিস অহরিহ দেখতে পাবে। 😀
(জিনিসটা আমাদের ট্যাক্সের ক্ষেত্রেও খাটে। 😛
উপস্থিত ধনসম্পদ বেশি হলে ট্যাক্স ও বেশি :v )
তবে এটা ভেবে রেখোনা যে,প্রকৃতি কেবল উপরের এক কথায় প্রকাশটা মানলেই,e ক্ষমতায় আসে!
e এর ক্ষমতার এলাকা আরো বড় B-)
এখন চল বিন্যাসের একটা জিনিস দেখি।
প্রকৃতিতে রেন্ডমলি সব কিছু বিন্যস্ত থাকার মধ্যেও রয়েছে e।
দেখতে চাউ??
চল দেখে নেওয়া যাক।
ধর আমরা কিছু মানুষকে এক লাইনে সাজাব।ধর তিনজন।তাদের নাম দিলাম আমরা A,B ও C
এখন আমরা এদের মোট সাজানোর বের করব।
এদের মোট সাজানোর সংখ্যা 6 (খাতায় লিখে লিখে গুনেই দেখ যারা ইন্টারের বিন্যাস সমাবেশ পর্যায়ে পৌছাউনি)
এদের একজনকেও নিজ নিজ জায়গায় না রেখে সাজানোর সংখ্যা 2
(মানে A তার আগের জায়গাটাতে মানে প্রথম স্থানে থাকবে না।B ও C এর ক্ষেত্রেও একইরকম)
এখন 6÷2= 3
যদি চারজন নিতাম
(ABCD) তবে এর অনুপাতের মান আসত 2.66666……(24÷9)
যদি তেরোজন নিতাম(আনলাকি সংখ্যাই নিলাম B-) )
(ABCDEFGHIJKLM) তবে এই অনুপাতের মান আসত
2.718281829….(6227020800÷2290792932)
বোঝনাই ব্যাপারটা?? 😛 নীচের ছবিটা ভালভাবে দেখ কয়েকবার।আর একটু গুনেও দেখত পার ছবির প্রথম দুইটা এক্সাম্পল।

কি!!বুঝলে??
এই অনুপাতটার মান ক্রমশ e এর দিকে অগ্রসর হচ্ছে।
প্রকৃতি এরকম অসংখ্য কিছু রেন্ডমলি সাজিয়ে দিচ্ছে প্রতিনিয়ত।অনু পরমাণু থেকে ফুলের রঙ সব ক্ষেত্রেই।
দেখলে তো e তার ডিএনএ কোথায় কোথায় রেখে গেছে? 😛
এবার সম্ভাবনা বিষয়ে আসি।
এই সম্ভাবনা জিনিসটা সম্পর্কে যাদের খুব একটা জানা নেই তাদের একটু ক্লিয়ার করে দেই।
আগেই বলে দেই কোনো কিছুর সম্ভাবনা 0.5 বা ৫০% মানে এই যা যে,প্রতি দুই বারে একবার এটা ঘটবেই।
তবে যদি প্রায় অসীমসংখ্যক বার এক্সপেরিমেন্ট করা হয় তখন বলা যায় অনুকূল ফলাফল মোট ফলাফলের অর্ধেক হবে।
(এক্সপেরিমেন্ট অসীম হলে প্রায় শব্দটা আর বসানো লাগেনা 🙂 )
ঠিক ধরেছো সম্ভাব্যতা মানেই
অনুকূল ফলাফল÷মোট সম্ভাব্য ফলাফল
😀
ধর একটা ছক্কার ডাইসের ব্যাপারে।
এখন ডাইস ছোড়া হলে ছয়টা সম্ভাব্য নাম্বারের থেকে যেকোন একটি আসবেই।
তাহলে ধর ৩ উঠার সম্ভাবনা হবে 1/6
আর ৩ না আসার সম্ভাবনা হবে 5/6
(অর্থ্যাৎ ঘটা+না ঘটা =1)
ধর এখন ছক্কাটা ছয়বার নিক্ষেপ করব।
হিসেব করব কতভাবে ১ না আসতে পারে।
প্রথমবার নিক্ষেপে 5 টা অপশন ১ না আসার।
একইভাবে দ্বিতীয় বারেও 5 টা এভাবে
মোট ছয়বার মারলে ১ না আসার মোট বিন্যাস ঘটানো যায় 5x5x5x5x5x5 ভাবে।
মোট সম্ভাব্য সকল ঘটনার অপশন 6x6x6x6x6x6
সুতরাং ছয়বার ছক্কা নিক্ষেপে একবারও ১ না আসার সম্ভাবনা
5.5.5.5.5.5/6.6.6.6.6.6 = 0.3348
এখন মূল সমস্যায় আসি।
এখন আমি বিভিন্ন ধরনের ডাইস নিক্ষেপ করব 😀
এবং হিসেব করব ১ না উঠার সম্ভাবনা
এবং ডাইসটা যত পাশ বিশিষ্ট ততবার নিক্ষেপ হবে আমি আবার বলছি “ডাইসটা যত পাশ বিশিষ্ট ততবার নিক্ষেপ” হবে।নীচের ছবিটা দেখ।

দেখলে তো?সম্ভাব্যতাটা ক্রমশ 1/e এর দিকে অগ্রসর হচ্ছে। 😀
এছাড়া ডিএরেঞ্জমেন্ট(ভুলভাবে সাজানো বলতে পার) অনেক ঘটনার সম্ভাবনার ক্ষেত্রে লুকিয়ে আছে এই e।
এছাড়া সকল প্রাকৃতিক সম্ভাবনা জগতে e এর নেতাগিরি চোখে পড়ার মত।
এবার চল সংখ্যাতত্ত্বে e এর একটা ছোট্ট কারিকুরি দেখি 😀
π(x) দ্বারা বুঝায় x ও x থেকে ছোট মৌলিক সংখ্যার সংখ্যা।
এবং মজার জিনিস হল
এর মান x/lnx এর প্রায় সমান।
(ln হল e ভিত্তিক লগারিদম এটা সবাই জানো আশা করি)
প্রায় সমান বললে e কে অসম্মান করা হয়ে যায়।আসলে বলা উচিত x এর সমান যত বাড়তে থাকে x/lnx এর মান তত নিখুত হতে থাকে 😀
মানে আরো পরিষ্কার ভাবে বললে, x এর মধ্যে randomly একটা সংখ্যা বেছে নিলে তার মৌলিক সংখ্যা হওয়া সম্ভাবনা
1/lnx
গ্রাফটা দেখে নিতে পার।
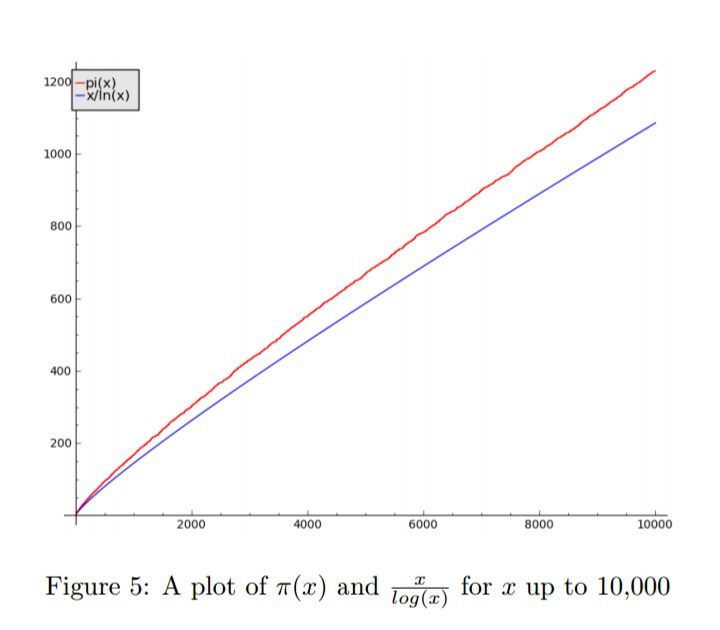
বিন্যাস,সম্ভাবনা,সংখ্যাতত্ত্ব থেকে সরে চল এখন প্রকৃতির আরো অনেকটা কাছে যাওয়া যাক।
এসবের খুব একটা details ব্যাখ্যায় যাব না।
তবে জিনিসগুলা অনুভব করার চেষ্টা আমরা। 😀
চল তার আগে একটা ফাংশনের সাথে পরিচত হওয়া যাক।
y=f(x) = ex
এই কার্তেসীয় সিধাসাধা সমীকরণটির সাথে অনেকেই পরিচিত। 😀
একে গ্রাফ পেপারে plot করলে কেমন হয় দেখ।
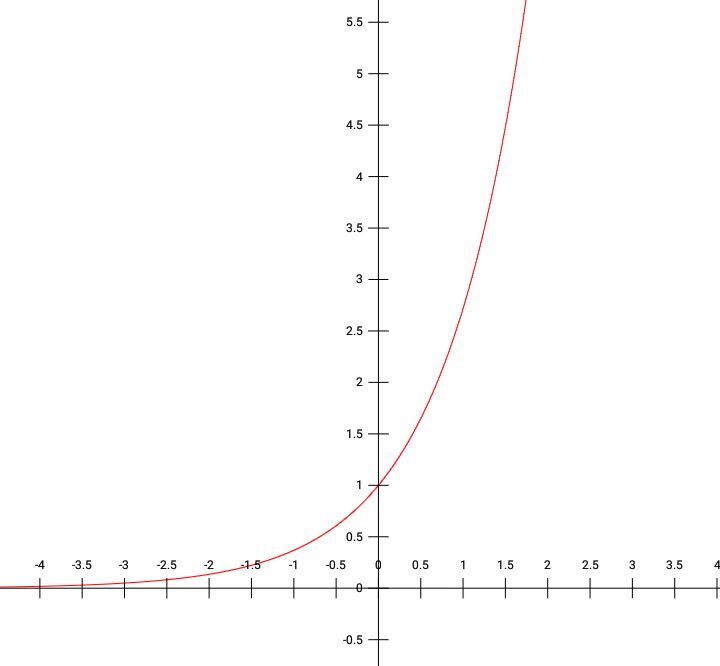
এটাও অনেকেই জানো।ক্যালকুলাসে দেখেছো ইতোমধ্যে অনেকেই।
তবে আমার মনে হয় না,সবাই এই সমীকরণের পোলার আকারের সাথে খুব একটা পরিচিত আছ!!
এর পোলার আকার

এটা বেহুদা এনে জটিলতা বাড়ানোর কারণ জানতে চাইছো??
আগে এর গ্রাফটা দেখ নীচের ছবিতে।
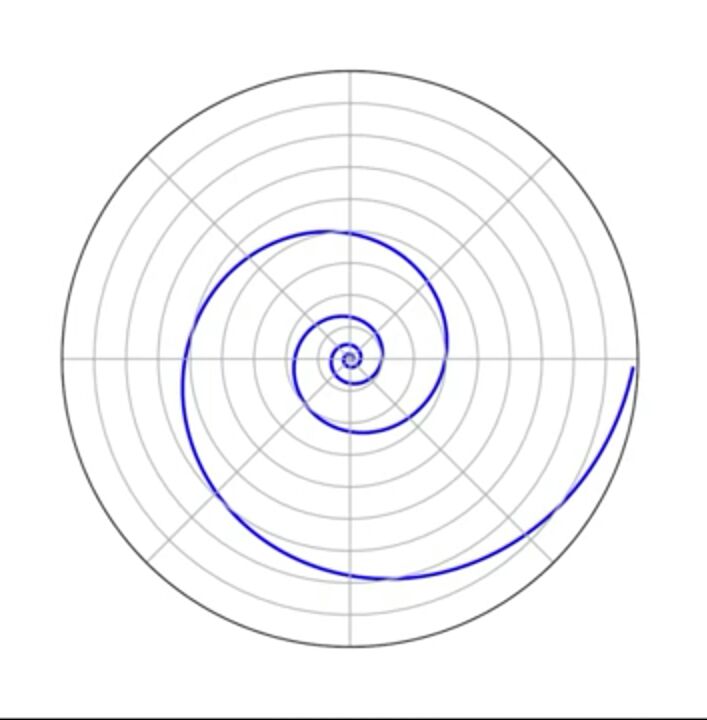
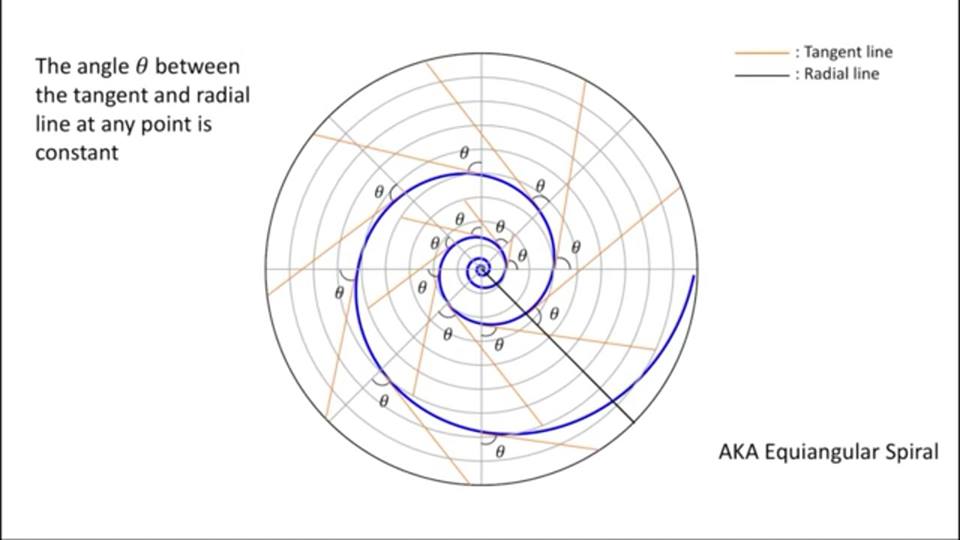
(প্রথম ছবিটার পরও একটা মজার ফ্যাক্ট দেখিয়ে দেওয়ার জন্য দ্বিতীয় ছবিটাও দেওয়া)
অনেক উৎসাহী পাঠক হয়ত লাফিয়েই উঠবে।বলবে “এতো গোল্ডেন রেশিও রিলেটেড”
অনেকে বলবে “শামুকের খোল”
হ্যা হ্যা সবই ঠিক আছে। 😀
শুধু শামুক বা গোল্ডেন রেশিও নয় টর্নেডো,ফুল,ফল এমনকি “মোনালিসা” ছবিটিতেও আছে এই গ্রাফটির প্রভুত্ব!
একে বলা হয় “লগারিদমিক স্পাইরল”
কয়েকটা পরিচিত জায়গায় লগারিদমিক স্পাইরল দেখ।

এমনকি পোকামাকপড়েরা আগুনে পুড়ে মরে তার পেছনেও এই “লগারিদমিক স্পাইরল” রয়েছে। 😀
একটা জিনিস খেয়াল করেছো কিনা জানিনা।কখনো কি ভেবেছো পোকামাকড়েরা আলো বা আগুন দেখলেই ঝাপিয়ে পড়লেও সূর্য বা চাদের দিকে যাওয়ার চেষ্টা করেনা কেন? :v
আসলে পোকামাকড়েরা আলোর সাথে একই কোণ তৈরী করে চলে।
সূর্যের বা অনেক অনেক দূরের কোনো আলো প্রায় সমান্তরাল ভাবে আসে আসে।তাই সে সূর্যের দিকে ছুটে যায় না।
কিন্তু কোনো কাছের light source এর ক্ষেত্রে ব্যাপারটা ভিন্ন।
বেশিকিছু বলে জটিলতা বাড়াব না শুধু নীচের ছবিগুলো দেখো।
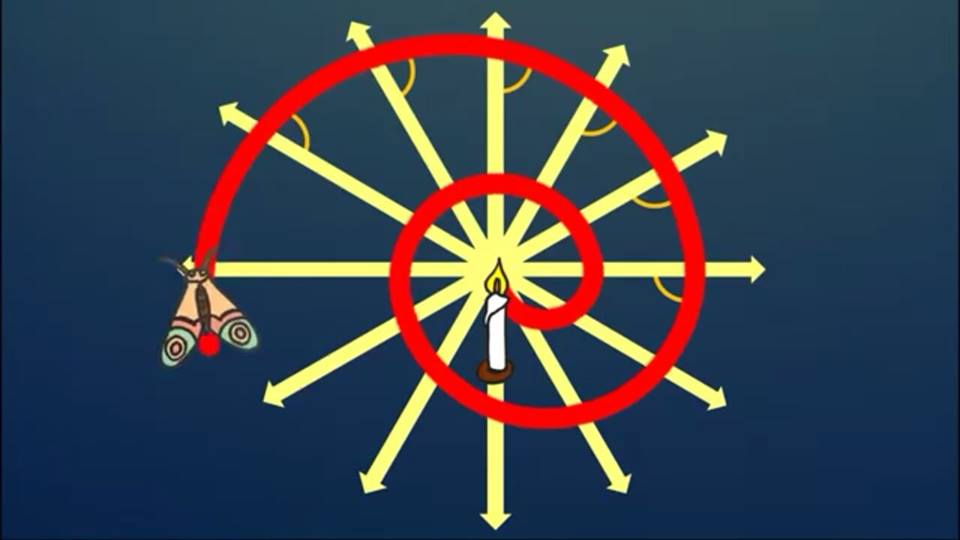


(আগ্রহটা বাড়িয়ে দিয়ে যাচ্ছি।ঘেটেঘুটে জেনে নেওয়াটা তোমার দায়িত্ব।)
একটা বালতি থেকে ফুটো দিয়ে পানি পড়ার হার থেকে শুরু করে রেন্ডম প্রোবাবিলিটি কিংবা গানের সুর কিংবা তারার আলোর উজ্জ্বলতা ও দূরত্বের সাথে সম্পর্ক,কিংবা জনসংখ্যা বৃদ্ধির হার,সম্ভাব্যতা,প্রকৃতি,এমনকি মানুষের আচার আচরণের ক্ষেত্রেও,আরো আছে টর্নেডোর শেইপ,এন্ট্রপি কিংবা…….
থেমেই যাই।কি বলো!?
কিবোর্ড আর আমার আঙ্গুলের উপর রেহাই দিলাম নাহয় একটু!! _
এখন একটা ছোট্টো ইকুয়েশন দিয়ে শেষ করব বিশাল এই “লিখিত বকবক”
ঐযে শুরুতেই বলেছিলাম পৃথিবীর সব থেকে সুন্দর একটা ইকুএশন।
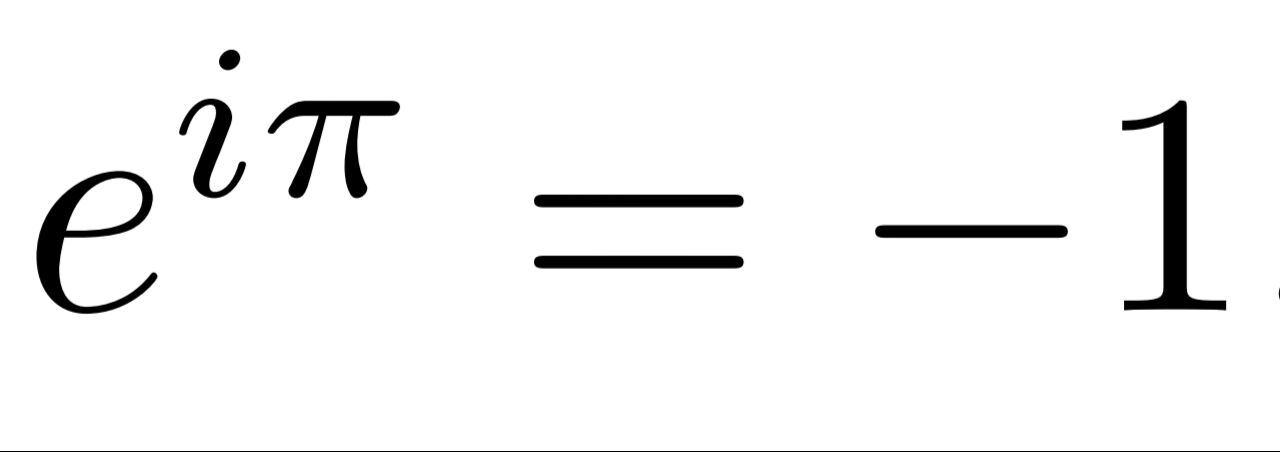
এটার প্রমাণ আমি দেখাব না।
আপাতত এর সৌন্দর্য্যেই সীমাবদ্ধ থাকি।
তবে যারা প্রমাণ চাও তারা ক্যালকুলাস আর ম্যাকলরিনের সাহায্য নিতে পার।
ইকুএশনটা কতটা সুন্দর কিছু না বুঝেই শুধু এতে ব্যবহৃত সংখ্যা গুলো দেখেই বলা যায়।
π আর e দুটো অমূলদ সংখ্যা,i কাল্পনিক সংখ্যা(i=√-1)
আর -1 একটি বাস্তব মূলদ সংখ্যা। 😀
একটা ইকুয়েশনেই সংখ্যা জগতের সকল রহস্যময় জিনিস!!
এই ইকুয়েশনটা নিয়েও অনেক fact আছে।সেসবের ধারে কাছেও যাব না এখন আমি।যাওয়াটা তোমাদের দায়িত্ব। 😀
কিছু বুঝাতে পেরেছি কিনা জানিনা।
কিছু বুঝাতে পারি আর না পারি একটু হলেও যদি অনুভব করাতে পারি,সত্যিই ভাল লাগবে।
ভাল থেকো সবাই। 🙂
তোমাদের জীবন হোক সংখ্যার মতই সুন্দর আর নিষ্পাপ। 🙂
বিদায় এই পর্বে।
বি:দ্র: এই লেখাটি লেখার জন্য গুগল,বইপুস্তক ও দুটি মাতৃভাষার যাচ্ছেতাই ব্যবহার করা হয়েছে।ক্ষমাত্রুটি ভুলসুন্দর দৃষ্টিতে দেখবেন। 😛

লেখাটা অনেক চমৎকার হয়েছে ভাই 😀
অসাধারন to the power “e”!!!