মনে করি আমাদের বলা হল,
x+2y = 5
3x + 7y = 17
এই ২ টা সমীকরনের অজ্ঞাত রাশির মান বের করে দিতে । যেটা সমাধান করা কোন ব্যাপারই না । আমরা প্রতিস্থাপন,অপনয়ন, নির্ণায়ক অনেক অনেক নিয়মে সমাধান করে ফেলতে পারি ।
আচ্ছা এখন বলা হল,
x + y + z = 10
3x + 5y + 7z = 56
11x + 13y + 5z = 86
এই তিনটা সমীকরণ থেকে (x,y,z) এর মান বের করে দিতে । আমরা এটাও কষ্ট করে হলেও যেমনে হোক বার করতে পারব ।
তবে যদি আমাদেরকে ৪,৫,৬,,,,,,,,n এরকম অনেকগুলা ভ্যারিয়েবল এর অনেকগুলা ইকুয়েশন দিয়ে এদের সমাধান বের করতে বলে , তাও আমরা আমাদের প্রতিস্থাপন, নির্ণায়ক, অপসারণ এগুলো দিয়ে করতে পারব । কিন্তু করতে গিয়ে আমাদের দিনফুরিয়ে যাবে ।
কিন্তু এই সমস্যা টিকে আমরা “অপসারণ পদ্ধতি” আর “ম্যাট্রিক্স” ব্যবহার করে অনেক দ্রুতগতিতে আর অনেক সহজে সমাধান করে ফেলতে পারি । যার নাম গাউসিয়ান এলিমিনেশন ।
আমরা সমস্যাটিকে এভাবে মডেলিং করি ।
1 * x + 1 * y + 1 * z = 10 ………………(1)
3 * x + 5 * y + 7 * z = 56……………..(2)
11 * x + 13 * y + 5 * z = 86 ……………..(3)
আমরা এখন চাইব , প্রত্যেক সমীকরণে একটা চলক রাখতে তাহলে তো খুব সহজে মান বের করে ফেলতে পারতাম তাই না ?
তাহলে আমরা এখন চাই (2) এবং (3) এই দুইটা সমীকরণে, x কে অপসারণ করতে । কীভাবে করব ?
x + y + z = 10
0 + (5 – 1 * 3/1) + (7 – 1 * 3/1) = 56 – 10 * (3/1) ; [2 নং থেকে ১ * ৩ বিয়েগ করে]
0 + (13 – 1 * 11/1) + (5 – 1 * 11/1) = 86 – 10 * 11 / 1 [৩ নং থেকে ১ * ১১ বিয়োগ করে ]
এখন আমরা পাই,
x + y + z = 10…………………(1)
0 + 2y + 4z = 26……………….(2)
0+ 2y – 6z = -24……………….(3)
এভাবে আমরা আমাদের সমীকরণগুলোকে রিডিউস করতে পারলাম । এরপরে আমরা এবার y গুলোকে কমাই । আমাদের মূল টার্গেট হল কর্ণ বরাবর চলকগুলোকে রাখা । আর বাকি সমীকরণে চলকগুলোর সহগ শূন্য করে ফেলা । এতে আমরা অনেক সহজে মানগুলো বের করতে পারব । তাহলে আমাদের লক্ষ্য প্রথম সমীকরণে শুধু x, ২য় সমীকরণে শুধু y আর তৃতীয় সমীকরণে শুধু z রাখা । আর এজন্যই আমরা নিচের সমীকরণ গুলো থেকে x কে ভ্যানিস করেছি । তাহলে এখন যেহেতু আমরা ২ য় সমীকরণে শুধু y এর মান রাখব তাই এর নিচের সবগুলো থেকে y অপসারণ করি ।
এতে যেটা করতে হবে সেটা হলো (৩) – (২) * ১ করার পরে আমরা পাই ,।
x + y + z = 10
2y + 4z = 26
-10z = -50
তো আমরা এখন যেই কাজগুলো করলাম সেগুলো তো ম্যাট্রিক্সে মডেলিং করেও করতে পারতাম । কীভাবে ?
(Are you watching closely ? )
আমাদের সমীকরণগুলোকে একটু লক্ষ্য করি । 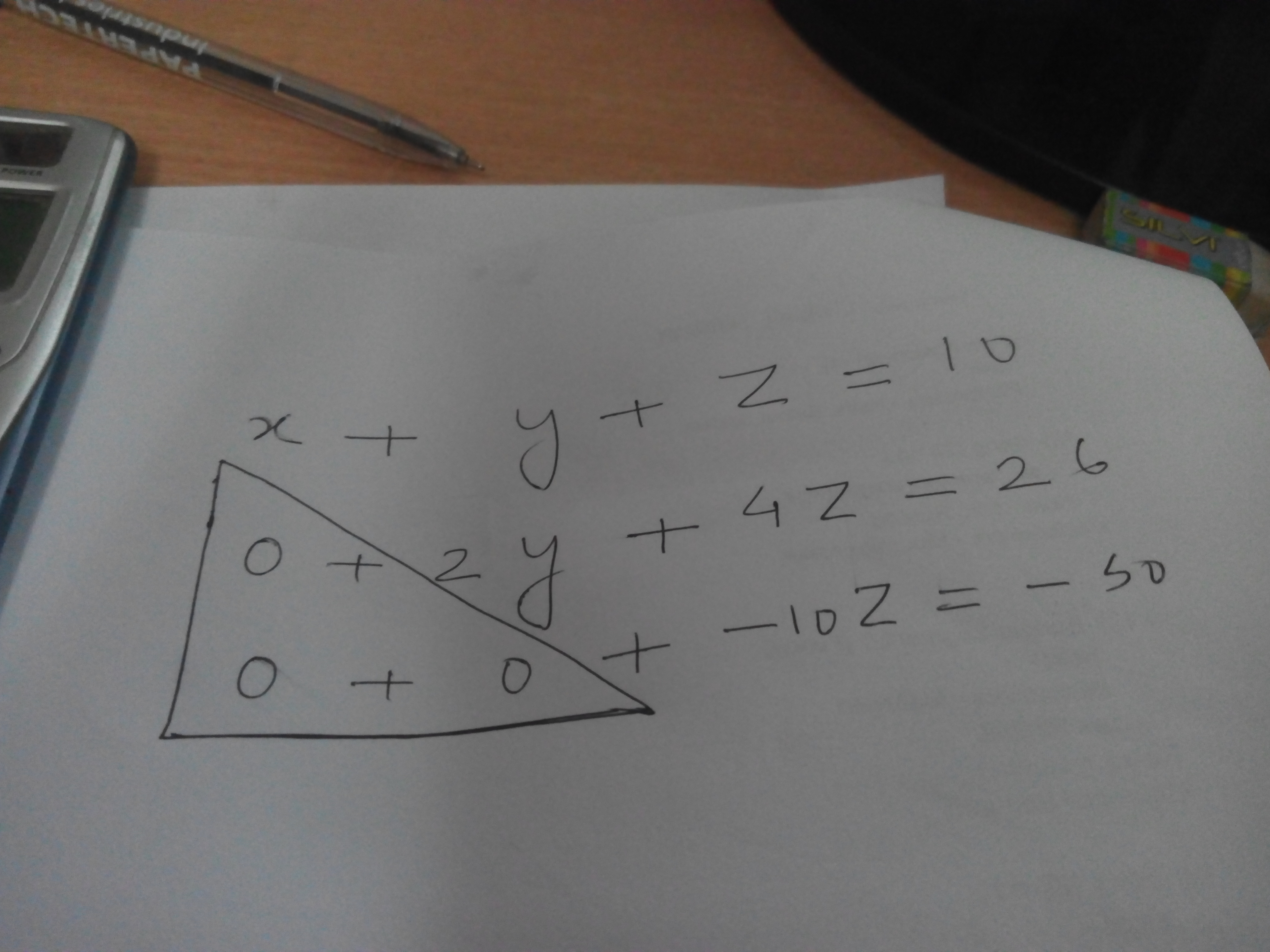
সমীকরণগুলোর কেবল একটা পাশে সহগের মান আছে আর বাকি আরেকপাশে সহগগুলোর মান শূন্য । একটু খেয়াল করলেই দেখব । পুরো ফরম্যাট টা একটা ট্রাইঅ্যাঙ্গুলার বা ত্রিভুজাকৃতি ফরম্যাট নিয়েছে । কারণ নিচের সমীকরণে একটা উপরেরটাতে তার থেকে আরেকটা বেশি, এর উপরেরটাতে আরো একটা বেশি এভাবে আস্তে আস্তে চলকের সংখ্যা বাড়ছে , আর আস্তে আস্তে এটা একটা ট্রাই অ্যাঙ্গুলার ফরম্যাট এ দাঁড়িয়েছে । এই ট্রাই অ্যাঙ্গুলার ফরম্যাট থেকে আমরা যে কোন ইকুয়েশন সেট সমাধান করে ফেলতে পারি । কারণ দেখি একদম শেষ যেই সমীকরণ সেখানে চলক একটা, তার মান বের করি । আর তারপরে আমরা এর উপরের সমীকরণে যাই । এখানে ২ টা চলক একটা জানি, আরেকটা বের করি । এখন আমরা ২ টা চলকের মান বের করে ফেলেছি । এরপরে তার উপরেরটা তে যাই এখানে তিনটা চলক । দুইটা জানি এটা ও বার করতে পারি ।
এভাবে নিচে থেকে আমরা আস্তে আস্তে একেকটা চলক বার করে করে সবগুলো চলকের মান বের করতে পারি ।
আমরা এখন যেই কাজটা করলাম সেটাতে অবশ্যই একটা ট্রাইঅ্যাঙ্গুলার ফরম্যাটে প্রেসেন্ট করা লাগছে আর আস্তে আস্তে নিচে থেকে সলভ করতে হচ্ছে । এখন আমরা একটা কথা শুরু তে লিখেছিলাম “আমরা এখন চাইব , প্রত্যেক সমীকরণে একটা চলক রাখতে তাহলে তো খুব সহজে মান বের করে ফেলতে পারতাম তাই না ?”
এটা মানে হচ্ছে প্রতিটা সমীকরণে যদি কেবল একটা চলক থাকত , কর্ণ বরাবর চলকের সহগ গুলো শূন্যব্যতীত অন্য কোন মান থাকত আর বাকি প্রতিটা সমীকরণে বাকি প্রতিটা চলকের সহগের মান শূন্য হত । তাহলে কি আমরা একদম ডাইরেক্টলি সবগুলো মান বের করে ফেলতে পারতাম না ?
মানে এখন, যদি আমি আগের মত ই সহগের গুণ দাঁড়া চলক গুলোকে অপসারণ করে , প্রতিটা সমীকরণে শুধু কর্ণ বরাবর চলকগুলোকে রাখতাম তাহলে আমরা নিশচয় একদম সরাসরি মানগুলো বের করে ফেলতে পারতাম ।
5x = 10
5y = 15
-10z = -50
তাহলে নিশ্চয় আমরা আরো অনেক সহজে সমীকরণগুলোকে সমাধান করে ফেলতে পারতাম । এই ফরম্যাটে আনার জন্য ও আমাদের কাজ একই । আমরা প্রত্যেকবার একেকটা চলক রেখে বাকিগুলোকে অপসারণ করতে থাকি ।
তবে মূল স্টেপ এরকমঃ
আমরা প্রতিটা সমীকরণের ডায়াগনাল বরাবর চলকগুলোকে রাখি । আর বাকিসময় যেই সমীকরণ চলকটা রাখব । তার নিচের আর পরে উপরের সবগুলো সমীকরণে এই চলকের সহগগুলোকে শূন্য করে ফেলি ।
এরপরে তো শুধু মান বের করতে পারলেই কাজ শেষ ।
ম্যাট্রক্সে মডেলিংঃ
এখন সব থেকে ইন্টেরেস্টিং পার্ট । সমস্যাটিকে ম্যাট্রিক্সে মডেলিং করা ।
আমাদের ইকুয়েসশন গুলোকে কি এভাবে লেখা যায় :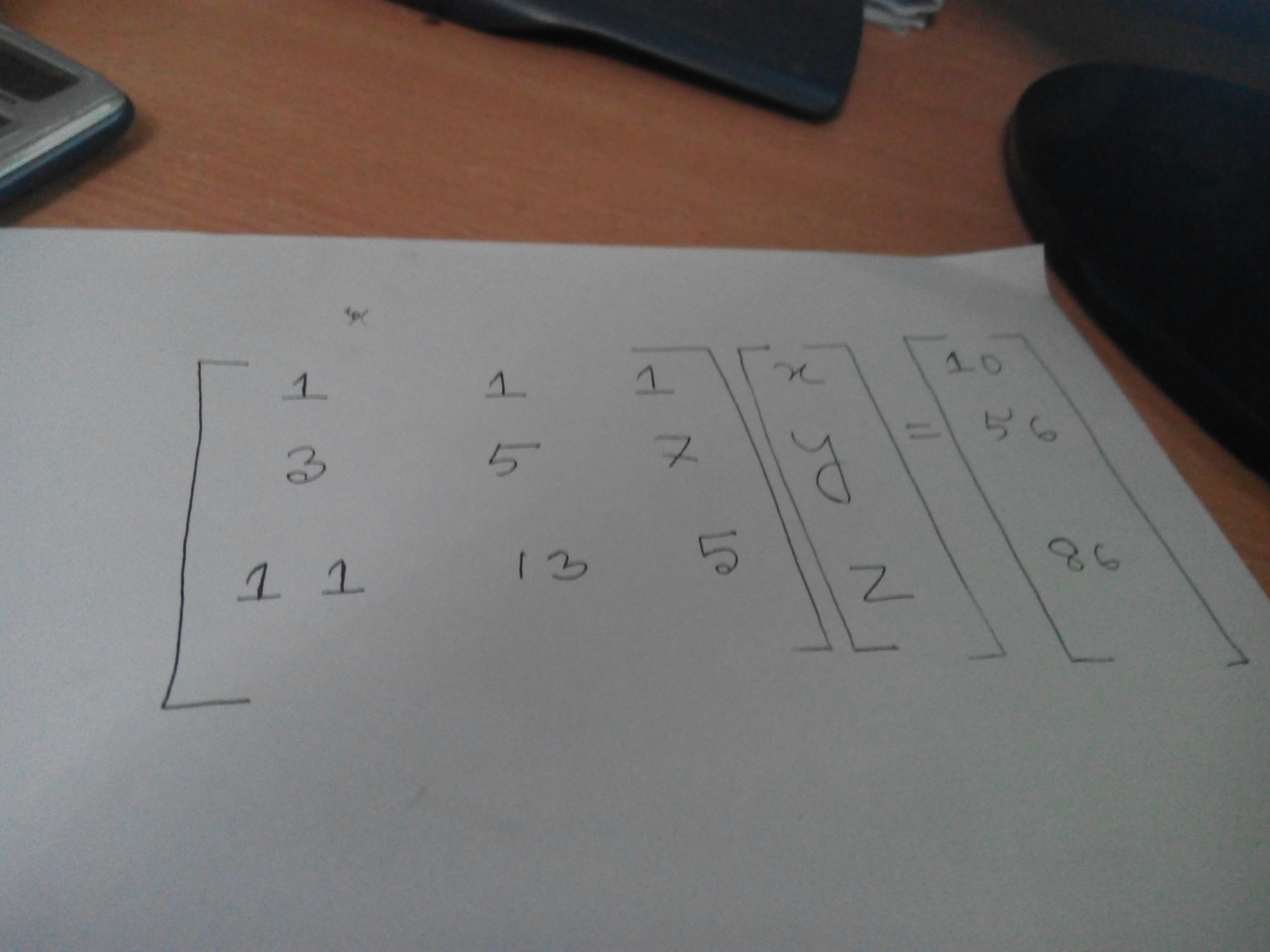
এখন আমরা নরমালি যেভাবে একটু আগে রিডিউস করেছিলাম সেভাবে কি করতে পারি না ?
যেমন (i তম ম্যাট্রিক্সের k তম কলাম) * নতুন মাল্টিপল থেকে বিয়োগ হবে ( j তম ম্যাট্রিক্সের k তম কলাম) আর এই মানটাই (j,k) তম ঘরে বসবে এ। এভাবে বিয়োগ করে করে অথবা যোগ করে করে কি আমরা শুধুমাত্র ডায়াগনালে মান সাজিয়ে বসাতে পারি না ? ঠিক একই কাজগুলো যা আমরা অপসারণ করার সময়ে করেছিলাম এখন ম্যাট্রিক্সে রো কলামের কম্বিনেশন দিয়ে করতে পারব না ? ।
আমরা ঠিক এই কাজগুলোই করব । অলটাইম ডায়াগনালে মান রেখে তার উপরের আর নিচে সহগগুলোর মান শূন্য করব ।
কিন্তু মাথায় রাখা লাগবে, যেহেতু আমাদের সমীকরণে ডান আর বাম দুই পাশে আছে তাই কাজ করলে দুই পাশেই করতে হবে । মানে বামপাশে যেই রো থেকে যেই রো যেভাবে বিয়োগ হচ্ছে ডানপাশেও ঠিক একই ভাবে করা লাগবে । কর্ণ বরাবর এলিমেন্টগুলোকে বলা হয় পিভট এলিমেন্ট । আমাদের মূল লক্ষ্যই হল পিভটগুলা ঠিক রাখা । আর বাকি সবগুলোকে রিডিউস করা ।
আর এভাবে আমাদের চিরপরিচিত সমীকরণগুলোকে আমরা আমাদের পরিচিত ম্যাট্রিক্স আর অপনয়ন পদ্ধতির ডিফরেন্ট কম্বিনেশন দিয়ে অনেক সহজে আর সিস্টেমেটিক সমাধান করতে পারি ।
গাউসিয়ান এলিমিনেশন সিস্টেম দিয়ে লিনিয়ার ইকুয়েশন সলভ করার নিয়ম টি বেশ অসাধারণ । কারণ এই কনসেপ্ট এ আমরা যে কোন n চলকের সমীকরণ সমাধান করতে পারি । কিন্তু মাথায় রাখতে হবে যদি কখনো কর্ণে পিভটের মান শূন্য হয়ে যায় তাহলে এই সমীকরণ সেটের কোন ইউনিক সমাধান নেই । এখানে তখন কোন প্যারালাল লাইন আছে যা কোনদিন ছেদ করবে না ।
নিচে আমি গাউসিয়ান এলিমিনেশন দিয়ে n চলকের কোন ইকুয়েশন সলভ করার সি++ পোগ্রাম দিচ্ছি । আশা করি আগে সবাই একবার এটা ইম্পিমেন্ট করার ট্রাই করব । না পারলে নিচের কোড দেখতে পারি ।
