আজকে আমরা মূলত একটা প্রবলেম নিয়ে আলোচনা করব । প্রবলেমটি বুঝতে খুব সোজা আর এর সমাধানটাও অনেক মজার । প্রবলেমটি হলঃ
আমাদের একটা পলিগন দেয়া থাকবে । পলিগন দেয়া থাকবে মানে হল, পলিগনটি যেই কো-অর্ডিনেট দিয়ে ফর্ম করে সেই কোঅর্ডিনেটগুলো সিকুয়েন্সালি দেয়া থাকবে (ক্লকওয়াইজ অথবা অ্যান্টিক্লকওয়াইজ) । এরপরে আমাদের কিছু কোয়েরি পয়েন্ট দেয়া থাকবে । আমাদের বলতে হবে যে পয়েন্টটি পলিগন এর মধ্যে না বাইরে ।
একটা ছবি দিলে প্রবলেমটা বুঝতে সুবিধা হবে ।
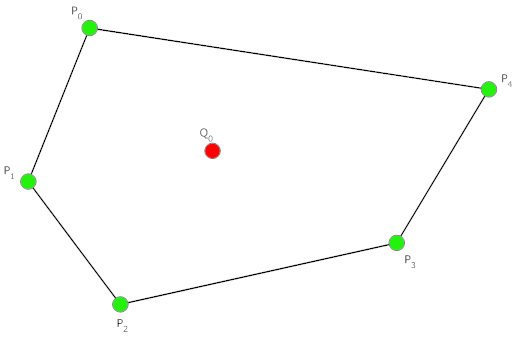
যেমন এখানে আমাদের একটা পলিগন দেয়া আছে । আর একটা পয়েন্ট দেয়া আছে q, যা পলিগন এর ভেতরে ।
তো আমাদের এই প্রবলেমের বেশ সুন্দর একটা সমাধান আছে । সমাধানটা এরকম, আমরা একটু হাতে কলমে কয়েকটা পলিগন আঁকি, আর এরপরে আমরা পলিগন এর মধ্যে কিছু পয়েন্ট নেই এবং সেটা থেকে অনেক দূরের কোন বিন্দু পর্যন্ত কিছু লাইন/ রেখাংশ টানি । ঠিক একইভাবে বাইরে কিছু পয়েন্ট নেই আর যে কোন দিকে অনেক দূর পর্যন্ত কিছু লাইন/রেখাংশ টানি ।
আমরা একটা জিনিস খেয়াল করব আমরা যদি কোন পয়েন্ট ভেতরে নেই আর তারপরে তার থেকে যে কোন দিকে রেখাংশ টানি (অবশ্যই অনেক দূরের কোন বিন্দু পর্যন্ত) তাহলে সে রেখাংশটি অবশ্যই অবশ্যই পলিগনটিকে বেজোড় সংখ্যকবার ছেদ করবে । আর যদি পয়েন্টটি বাইরে হয় সে ক্ষেত্রে জোড় সংখ্যক বার ছেদ করবে । কেন করবে ?
খুব সিম্পল লজিকে আমরা দেখি, যদি পয়েন্টটি বাইরে হয় তাহলে আমরা তার থেকে যে কোন দিকে যদি কোন রেখাংশ টানি, সেই রেখাংশটি হয় পলিগনটিকে ছেদ করবেই না ( পলিগন এর বিন্দুগুলো যে দিকে আমরা সম্পূর্ণ বিপরীত দিকে রেখাংশ টানছি) অথবা অনেক দূরের কোন পয়েন্ট হলে তাকে অবশ্যই পলিগনটিকে ছেদ করে তারপরে আবার বের হতে হবে মানে সর্বদা জোড় সংখ্যক পলিগন এর বাহুকে ছেদ করবে , এর জন্যই দূরের পয়েন্টটিকে অবশ্যই অনেক বেশি দূরে নিতে হবে, পলিগনটি যেই পয়েন্টগুলো দ্বারা ফর্ম করে তাদের থেকে অনেক বেশি দূরে । কেন সর্বদা জোড় সংখ্যক বার ছেদ করবে ? একটু চিন্তা করলেই দেখবে যে, আমরা যখন বাইরে থেকে ভেতরে ঢুকছি আমাদের ” দূরের বিন্দুটি” পলিগন এর মধ্যে না , তাই আমাদের কি করতে হবে একবার ঢুকে সেই বিন্দুটি পর্যন্ত পৌছাতে হলে রেখাংশটি/ রে টিকে অবশ্যই পলিগন এর বাইরে বের হতে হবে । এভাবে প্রতিবার ঢুকতে হলে আবার বের হতে হবে মানে জোড় সং খ্যক বার পলিগনটিকে ছেদ করতে হবে ।
এভাবে জেনারেল কেস এ প্রবলেমটি সল্ভ হবে । এখন স্পেশালি সিনেরিওগুলোতে আসি ।
আচ্ছা আমি তো লাইন টানছি আর এর পরে হিসেব করছি যে, সেটা কতবার ছেদ করছে তাই না ? কিন্তু খেয়াল করে দেখ যদি এটা লাইনটানার সময় পলিগন এর কোন ভার্টেক্স দিয়ে যায় ? তাহলে তো আমরা সেম জিনিস কে ২ বার হিসেব করব তাই না ? আমাদের সমাধান তো বলবে যে ভেতরে নেই কারণ জোড় সংখ্যক বার ছেদ তাহলে ? তাহলে আমরা একটা কাজ করতে পারি আমরা হিসেব করে বললাম যে ঠিক আছে ভার্টেক্স দিয়ে গেলে আমরা বলব যে হা, একবার নিব (মোট যতবার ভার্টেক্স ছেদ করবে / ২) । অন্য সময় নরমালি হিসেব করব বা যোগ করব । আর মোট যদি বেজোড় হয় তাহলে বলব ভেতরে আর জোড় হলে বাইরে । এটাও কাজ করবে না কারণ দেখি ।
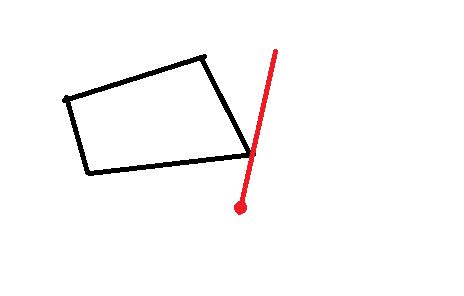
এক্ষেত্রে তো বেজোড় সংখ্যকবার ছেদ করেছে আমাদের হিসেবে পয়েন্টটি তো মধ্যে থাকার কথা কিন্ত ভেতরে না সেটি বাইরে । তাহলে ?
আচ্ছা এই সমস্যা সমাধানের সবচাইতে ভাল উপায় হচ্ছে, এমনভাবে দূরের পয়েন্ট টা নেয়া যাতে কোন ভাবে কোন লাইন/রে/রেখাংশ টানলে সেটা ভার্টেক্স দিয়ে না যায় । তাহলে তো একবার নিব না দুইবার নিব সেই প্রবলেম এ পড়তে হয় না । তাই না ?
তাহলে আমাদের কাজ হবে আমাদের কোয়েরি পয়েন্ট সাপেক্ষে সবগুলো পলিগন এর পয়েন্ট এর স্লোপ বের করা । আর এরপর এমন স্লোপ সিলেক্ট করে দূরের পয়েন্ট নেয়া যাতে কোনভাবেই সেটা কোন ভার্টেক্স দিয়ে না যায় বা যেই স্লোপ টা কে আমি আমার ইনপুট থেকে পাচ্ছি না । আচ্ছা এখন [-৯০,৯০] এই পুরো রেঞ্জ এর মধ্যে কীভাবে আমি স্লোপ ঠিক করব ? সবচাইতে ইজি সলিউশন হল যেই ইন্টিজার স্লোপ পাই না সেটা কে নেয়া, আর সবথেকে ক্রিটিকাল কেস আমি যদি -৯০ থেকে ৯০ এর মধ্যে সব ইন্টিজার স্লোপ পাই তাহলে আমরা সবগুলো স্লোপ কে সর্ট করে যে কোন ২টা কনজি কিউটিভ স্লোপ এর মাঝের স্লোপ নিব । তাহলেই হবে । কারন সেটা অবশ্যই ইনপূট থেকে আসবে না ।
আমরা এটা থেকে লাইট ওজ এর Sleepwalking প্রবলেমটা সলভ করতে পারি । প্রবলেমটি সলভ করতে প্রবলেম হলে নিচের সলিউশনটা দেখতে পার ।
আমার সলিউশনঃ https://ideone.com/F2T0TQ
কৃতজ্ঞতা স্বীকারঃ
হাসনাইন হেইকেল জামি ।
রেজওয়ান মাহমুদ তন্ময় ।
রেফারেন্সঃ টপকোডার, উইকিপিডিয়া ।
