জন্মদিনের সম্ভাব্যতা ( Birthday Paradox নামেও খ্যাত) একটি বিখ্যাত ধাঁধা। ধাঁধা একারণে যে, এই সমস্যাটা’র গাণিতিক সমাধান আমাদের কমন সেন্স’কে বুড়ো আঙ্গুল দেখিয়ে দেয়; দেখিয়ে দেয় আমাদের চিন্তার অসারতা। সম্ভাব্যতা নিয়ে মাথা খাটানো প্রায় প্রত্যেকেরই পরিচিত এই সমস্যা’টা। কথা না বাড়িয়ে সমস্যা’য় যাওয়া যাক…
দুইজনের একই দিনে জন্মদিন হওয়ার সম্ভাবতাঃ
একটা রুমে কতজন থাকলে আমরা নিশ্চিতকরে বলতে পারি যে, কমপক্ষে দুইজনের জন্মদিন একই দিনে হবে?
উত্তরটা খুব সহজ – ৩৬৬ জন। কারণ, ৩৬৫ জনেরই আলাদা জন্মদিন থাকতে পারে (worst case)।
আচ্ছা তাহলে বলুন তো,
একটা রুমে কতজন থাকলে আমরা ৫০ ভাগ নিশ্চিত হতে পারি যে, এরুমে অন্তত দুজনের একই দিনে জন্মদিন?
কমন সেন্স কিংবা পূর্ব সমস্যার সূত্রধরে মনে হতে পারে যে, ৫০ ভাগ সম্ভাব্যতার জন্য হয়ত ১৮৩ জন মানুষ লাগবে। তাও এটাসেটা(exception) হিসেব করলেও হয়ত কমপক্ষে ১০০ জন লাগবেই?
কিন্তু আশ্চর্যজনকভাবে এর উত্তর ১৮৩ জনও না, ১০০ জনও না; এমনকি ৫০ জনও না…
একটা রুমে ২৩ জন, মাত্র ২৩ জন থাকলেই; যেকোন দুজনের একই জন্মদিনের সম্ভাব্যতা সম্ভাব্যতা ৫০% !!!
হ্যা গণিত আমাদের তাই বলে। গণিতের হিসেবে একটা রুমে ৫০ জন থাকলে এ জন্মদিনের সম্ভাব্যতা গিয়ে দাঁড়ায় ৯৭% এ (নিচের চার্ট দ্রষ্টব্য):
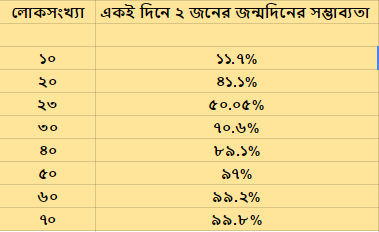
জন্মদিনের সম্ভাব্যতার চার্ট
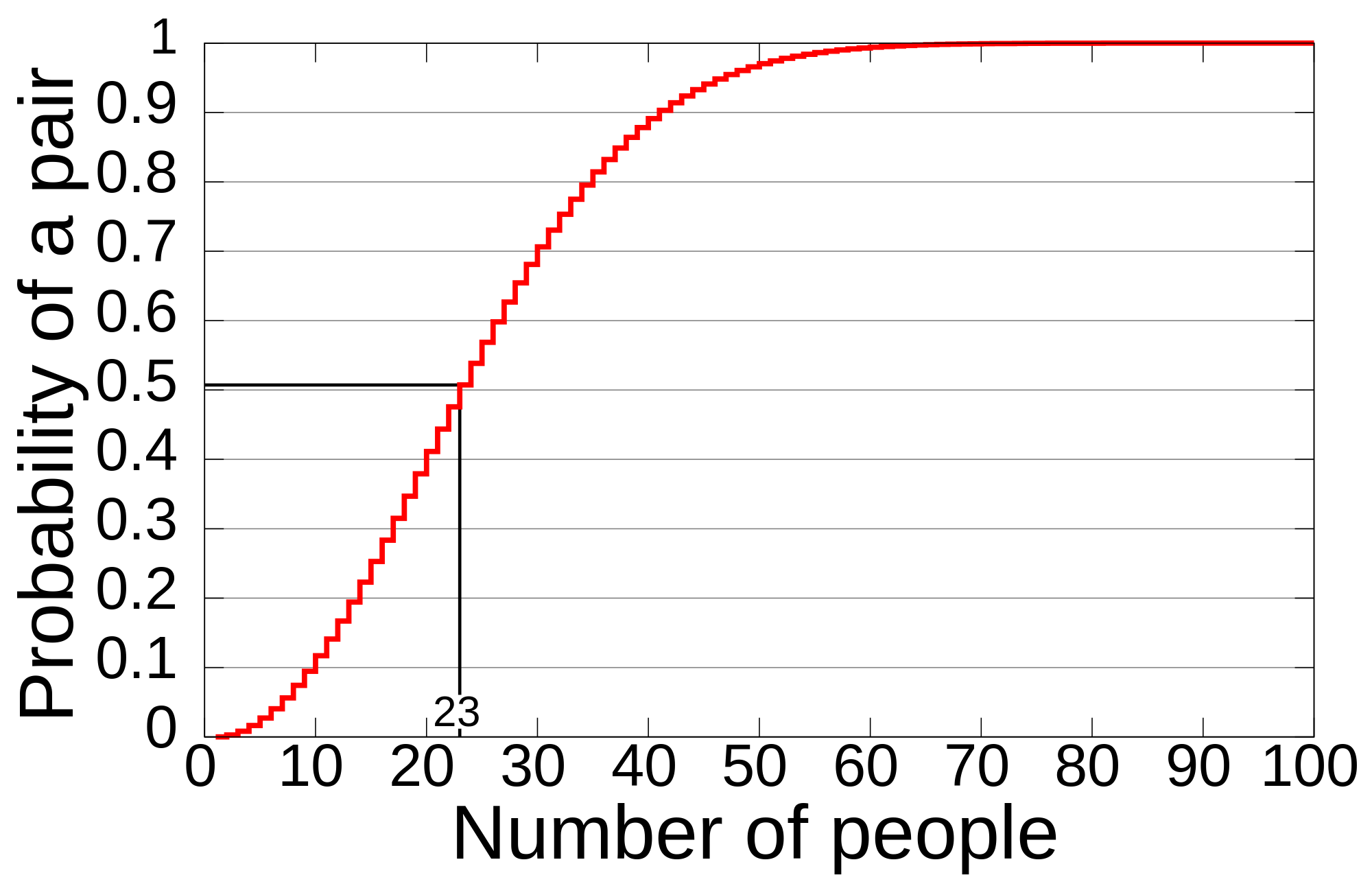
জন্মদিনের সম্ভাব্যতার গ্রাফ
আপাতদৃষ্টিতে সহজ এই সমস্যাটার কেন এত অদ্ভুত ফল আসে? চলুন দেখা যাক,
সমাধানঃ
“দুইজনের একই জন্মদিনের সম্ভাব্যতা” সমস্যাটা আমরা একটু উল্টো করে চিন্তা করতে পারি। অর্থাৎ, সমস্যাটা সমাধান করার জন্য আমরা উল্টো দিক থেকে অগ্রসর হতে পারি (using complement)। অর্থাৎ আমরা “দুইজনের একই জন্মদিন” এর সম্ভাব্যতা বের না করে, “দুইজনের আলাদা জন্মদিন” হওয়ার সম্ভাব্যতা বের করে ১ থেকে বিয়োগ করলেই পারি।
P(same birthday) = 1 – P(distinct birthday)
P(distinct birthday) বের করার জন্য আমরা নিচের মত পর্যায়ক্রমে একজন একজন করে যুক্ত করতে পারিঃ
১ম জনের জন্য, P1(distinct birthday) = 365/365 = 1; যেহেতু মানুষ একজন তাই তার জন্মদিন’টা অবশ্যই আলাদা (unique) হবেই।
২য় জনের জন্য, P2(distinct birthday) = 364/365 = 0.9973; যেহেতু ইতোমধ্যে রুমে একজন আছেন, তাই ২য় ব্যক্তির জন্মদিন আলাদা(distinct) হতে হলে অবশ্যই তার জন্মদিন বাকি ৩৬৪ দিনের মধ্যে হওয়া লাগবে।
৩য় জনের জন্য, P3(distinct birthday) = 363/365 = 0.9945; যেহেতু ইতোমধ্যে রুমে দুইজন আছেন, তাই ৩য় ব্যক্তির জন্মদিন আলাদা(distinct) হতে হলে অবশ্যই তার জন্মদিন বাকি ৩৬৩ দিনের মধ্যে হওয়া লাগবে।
৪র্থ জনের জন্য, P4(distinct birthday)= 362/365 = 0.9917; যেহেতু ইতোমধ্যে রুমে তিনজন আছেন, তাই ৪র্থ ব্যক্তির জন্মদিন আলাদা(distinct) হতে হলে অবশ্যই তার জন্মদিন বাকি ৩৬২ দিনের মধ্যে হওয়া লাগবে।
………
n তম ব্যক্তির জন, Pn(distinct birthday)= (365-(n-1))/365= (365+n-1)/365 ; যেহেতু ইতোমধ্যে রুমে n-1 জন আছেন, তাই n তম ব্যক্তির জন্মদিন আলাদা(distinct) হতে হলে অবশ্যই তার জন্মদিন বাকি (365-(n-1))= 365+n-1 দিনের মধ্যে হওয়া লাগবে।
তাহলে n সংখ্যক ব্যক্তির একইসাথে আলাদা আলাদা জন্মদিনের সম্ভাব্যতা হবে,

সুতরাং n সংখ্যক ব্যক্তির যেকোন দুইজনের একইদিনে জন্মদিনের সম্ভাব্যতা হবে,
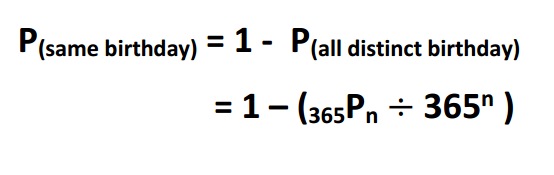
এই সমীকরণে n এর ভিন্ন ভিন্ন মান বসিয়ে আমরা সম্ভাবতা দেখতে পারি। n এর মান ২৩ বসালে সম্ভাব্যতা আসে ৫০.৭% । n এর ভিন্ন মানের জন্য জন্মদিনের সম্ভাব্যতা :

ভ্রম সৃষ্টি হওয়ার কারণ ও আরও একটি সমাধানঃ
এই সমস্যাটায় অধিকাংশ (সবাই 😛 ) মানুষেরই কমন সেন্স থুবড়ে পড়ে। এর কারণ হিসেবে বলা যায়, আমাদের মস্তিষ্ক সূচকীয় ক্যালকুলেশনে অভ্যস্ত নয়। আমরা সাধারণত লিনিয়ার সম্ভাব্যতার সমস্যাগুলো সমাধান করে অভ্যস্ত। আমরা খুব সহজেই আন্দাজ করতে পারি না যে, 230 কত বড় একটি সংখ্যা…। এ সমস্যার সমাধানে সূচকের উপস্থিতিই ভ্রমের মূল কারণ।
এই সমস্যাটায় আমাদের আন্দাজ ভুল হওয়ার কারণ হল আমরা অবচেতনমনে যেকোন একজনকে ফিক্সড ধরে তার সাথে বাকিদের জন্মদিন তুলনা করার চেষ্টা করছিলাম।
মনে হতে পারে, মানুষ ২৩ জন হলে আমরা একজনের সাথে বাকি ২২ জনের তুলনা করছিলাম, কিন্তু এই একজন যে যেকোন একজনই হতে পারে এটা আমাদের চিন্তার ফাঁক গলে বেরিয়ে যাচ্ছিল। আসলে ২৩ জন থাকলে আমরা ২২ টা নয়, আমরা C(23,2) =253 টি তুলনা করছিলাম। (প্রতিবারে ২ জন করে নিয়ে তাদের মধ্যে তুলনা করছিলাম) [দ্রষ্টব্যঃ C(23,2)= 23C2 ]
এভাবেও দেখা যায়, ১ম জনের সাথে বাকি ২২ জনের তুলনা+ ২য় জনের সাথে বাকি ২১ জনের তুলন+৩য় জনের সাথে বাকি ২০ জনের তুলনা……= (22+21+20+ …… +1) = 253
এই ২৫৩ টি জোড়ার নিজেদের মধ্যে তুলনা করলে কি দাঁড়ায় দেখা যাক,
আমরা আগেই দেখেছি,
১ জোড়া অর্থাৎ ২ জনের আলাদা দিনে জন্মদিন হওয়ার সম্ভাব্যতা P2(distinct birthday) = 364/365 ।
তাহলে ২৫৩ জোড়ার প্রত্যেক জোড়ার আলাদা দিনে জন্ম হওয়ার সম্ভাব্যতা,
= P2(distinct birthday).P2(distinct birthday).P2(distinct birthday)…..253 বার…
= (364/365).(364/365) .(364/365)……253 বার…
= (364/365)253
= 0.4995
সুতরাং ২৫৩ জোড়ার যেকোন এক জোড়ার একই দিনে জন্মদিন হওয়ার সম্ভাব্যতা,
= 1- 0.4995
=0.5005
=50.05%
মিলল তো?
তাহলে n সংখ্যক মানুষের জন্য সম্ভাব্যতা হবে,
= 1- (364/365)C(n,2) [ C(n,2) = nC2 ]
এটা আরও সহজ না? এই ফর্মুলায় n এর মান বদলিয়ে আমরা কাঙ্ক্ষিত সম্ভাবনা বের করতে পারি। তোমার ক্লাসে যদি ৬০ জন থাকে, তাহলে যেকোন দুইজনের একই দিনে জন্ম হওয়ার সম্ভাব্যতা,
= 1-(364/365)C(60,2) [ C(60,2) = 60C2 = 1770]
= 1-(364/365)1770
= 1-0.00778
= 0.9922
=99.2%
এই ৯৯ ভাগ নিশ্চয়তা তোমাকে গণিত ছাড়া আর কেউই দিতে পারবে না 🙂
আবার মনে করিয়ে দেই, সূচকীয় সম্ভাব্যতাগুলো আমরা মাথায় মাথায় চট করে করতে গেলেই মুখ থুবড়ে পড়ব; আমাদের মাথা সূচকীয় হিসেব নিকেশ এত সহজে করতে পারে না। তাই ধীরে সুস্থে দুই লাইন লিখে সমাধান করলেই আর বিভ্রান্ত হতে হবে না।
আচ্ছা রুমে কত জন থাকলে ৫০ ভাগ নিশ্চিত হবে যে, রুমে আরও অন্তত একজন আছে যার জন্মদিন তোমার জন্মদিনেই?? ২৩ জন কিন্তু এবার উত্তর নয়……
সম্ভাব্যতা নিয়ে আবারও আসব…অন্য কোন একদিন…

২৫৩ জন! Let p=364/365. ln(.5)/ln(p)=252.652.
এখানে ২৫৩ জন নয়, ২৫৩ টি তুলনার কথা বলা হয়েছে। আসলে আপনি কি বোঝাতে চাইলেন তা পরিষ্কার হল না। অনুগ্রহ করে আরেকবার বুঝিয়ে বললে ভাল হত; আর ভুল থাকলে, ধরিয়ে দিলে আরও ভাল হয় 🙂
<3
❤❤❤