বরফকে পানি বানিয়ে ইতি টেনেছিলাম গত পর্বের। আজ কঠিন খাবার লবণকে পানিতে দ্রবীভূত করার মাধ্যমে বিশৃংখলার সাথে শক্তির সম্পৃক্ততার যে আলোচনা তার শেষের শুরু করছি।
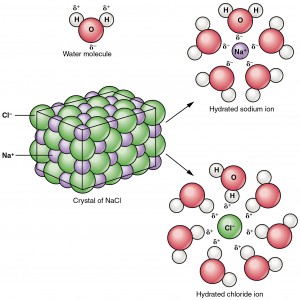
আমরা সবাই জানি খাবার লবণ (NaCl) একটি আয়নিক যৌগ যা কঠিন অবস্থায় কেলাস গঠন করে থাকে এবং ক্যাটায়ন ও অ্যানায়নগুলো তাতে সুনির্দিষ্ট সজ্জায় অবস্থান নেয়। এই লবণের স্ফটিক যখন পানিতে আসে তখন কী ঘটে? পানি (এক্ষেত্রে পরিবেশের মত কাজ করছে) হতে তাপ শোষণ করে ক্যাটায়ন ও অ্যানায়নগুলো তাদের মধ্যকার স্থির বৈদুতিক আকর্ষণকে ছিন্ন করে ও পানিতে চলে এসে পানিযোজিত (hydrated) হয়। পানিযোজিত হবার অর্থ, পানির অণুগুলো আয়নগুলোর চারপাশে এসে সম্মিলিতভাবে তাদের ঘিরে ধরে। নিচের চিত্র হতে বিষয়টি স্পষ্ট হয়ে আমাদের চোখে ধরা দেবে।
এ সবকিছুর সাথে বিশৃংখলাকে কি সম্পর্কিত করা সম্ভব? হ্যাঁ অবশ্যই! সুশৃংখল NaCl এর কেলাস ভেঙ্গে আয়নগুলোর পানিতে এসে হাইড্রেটেড হওয়া ও দ্রবণে এলোমেলোভাবে (random) ঘুরে বেড়ানোর স্বাধীনতা অর্জন তো বিশৃংখলা বৃদ্ধি পাওয়ারই নামান্তর। বলা যায়, পানি হতে লবণের কেলাস দ্বারা সেই শোষিত শক্তিই আসলে বিশৃংখলা বা এনট্রপি বৃদ্ধির পেছনে কলকাঠি নাড়ছে । তাহলে এনট্রপি বৃদ্ধির কারণ হিসেবে আবার শক্তির অফেরতযোগ্য স্থানান্তরকে আমরা দায়ী করতে পারলাম। পুরোনো প্রশ্ন, এই শক্তি অফেরতযোগ্য কেন? কারণ লবণ পানিতে রাখলে তা শক্তি গ্রহন করে দ্রবীভূত হওয়াই স্বাভাবিক, এর বিপরীত ঘটনা প্রকৃতিবিরুদ্ধ।
আচ্ছা, এতক্ষণ “বিশৃংখলা বাড়লেই এনট্রপি বাড়বে” নামক এই একই গীত আমরা যে মুখস্ত গাইলাম – এরও তো একটা ভৌত (physical) কারণ থাকা উচিত। বিশৃংখলার পরিমাপের সাথে এনট্রপি নামের রাশিটির সম্পর্ক দেখতে কেমন সেটা জানার আগ্রহ কি অনুভূত হয় না আমাদের? এবার তাহলে আমরা বিচরণ করার চেষ্টা করব আমাদের সিলেবাসের বাইরের সেই জগতে, যার জ্ঞান খুবই বেসিক হিসেবে কাজ করে এনট্রপি সম্পর্কে পরিষ্কার ধারণা রাখার জন্য। তিনটা শব্দের সাথে সর্বাগ্রে পরিচয় করিয়ে দেওয়া যাক – ম্যাক্রোস্টেট (Macrostate), মাইক্রোস্টেট (Microstate) ও মাল্টিপ্লিসিটি (Multiplicity)। এসব স্টেট ফেট আবার কীসের হয় রে বাবা!?! উত্তর হল – কোনো সিস্টেমের।
মাথার উপর দিয়ে যাওয়া এই কথামালাকে এখন একটু হজম করার চেষ্টা করি সবাই। সিস্টেম বলতে প্রথমেই গ্যাসভর্তি কোনো পিস্টনযুক্ত সিলিন্ডারের ভেতর ঢুকে দম বন্ধ হয়ে অজ্ঞান হবার দরকার নেই। দুইটি লুডুর ছক্কা (Dice) – এর মত নিরীহ দর্শন জিনিসও আমাদের সিস্টেম হতে পারে। নিচের চিত্রটি লক্ষ্য করা যাক –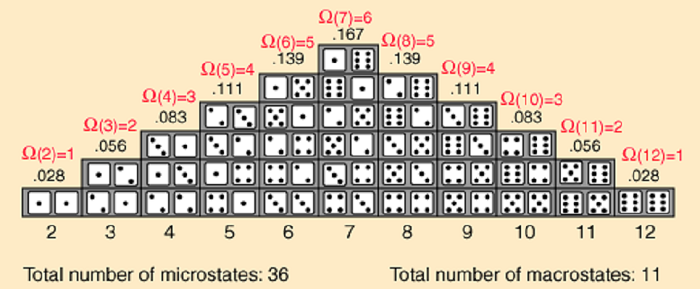
দু’টি ছক্কা যদি আমরা নিক্ষেপ করি তবে যতগুলো ফলাফল আসা সম্ভব তার সবগুলোই এই ছবিটাতে দেখানো হয়েছে। এখন একটু সতর্কতার সাথে আমরা আমাদের আলোচ্য বিষয়ে প্রবেশ করব। যদি ছক্কাগুলোর পিঠে থাকা সংখ্যাগুলোর সম্ভাব্য যোগফল নিয়ে আমরা চিন্তা করি তবে দেখতে পাব এই যোগফল ২ (যখন ছক্কা দু’টোর প্রত্যেকের পিঠে ১ করে থাকে) থেকে ১২ (যখন দু’টোর পিঠেই ৬) পর্যন্ত মোট ১১ ধরণের হতে পারে। এই যে ১১ ধরণের যোগফল আমরা পেতে পারি, এই যোগফলগুলোর প্রত্যেকটি একেকটি ম্যাক্রোস্টেট নির্দেশ করে। মানে যখন যোগফল ৭ পাব (সেটা হতে পারে ১+৬, ২+৫, ৩+৪, ৪+৩, ৫+২ বা ৬+১ ইচ্ছামত, ৭ হলেই হবে) সেটা এক ধরণের ম্যাক্রোস্টেট আবার যখন যোগফল ১০ পাব সেটা হবে আরেক ধরণের ম্যাক্রোস্টেট। ম্যাক্রো কথাটার অর্থ “বৃহৎ”, সুতরাং আমরা যখন ম্যাক্রোস্টেট নিয়ে কথা বলছি তখন আমরা এই দুই ছক্কা দিয়ে গঠিত সিস্টেমগুলোর প্রত্যেকটির সামগ্রিক অবস্থা (ছক্কাদের পিঠের সংখ্যার যোগফল) নিয়ে মাথা ঘামাচ্ছি, এক্ষেত্রে কোন ছক্কাটা পিঠে কত করে নিয়ে ঘুরছে তা আমাদের আলোচ্য নয়।
কিন্তু মজার ব্যাপার হল, একটা নির্দিষ্ট ম্যাক্রোস্টেটের মধ্যেও কিন্তু রকমফের হতে পারে যদি আমরা আরেকটু ভেতরে যেয়ে ছক্কাগুলোর ধারণকৃত সংখ্যার উপর আলোকপাত করি। এই যেমন ৭ যোগফলওয়ালা ম্যাক্রোস্টেট নিয়েই বলছিলাম, এই ম্যাক্রোস্টেট গঠন করা যায় ৬ টি ভিন্ন উপায়ে। একই ম্যাক্রোস্টেটে যতগুলো ভিন্ন ভিন্ন চিত্র আমরা পাই তাদের প্রতিটি হল একেকটি মাইক্রোস্টেট। যেমন ৫+২ যে মাইক্রোস্টেট বোঝায়, ৩+৪ বা ২+৫ সম্পূর্ণ আলাদা দু’টি মাইক্রোস্টেট নির্দেশ করে। এরা একই ম্যাক্রোস্টেটের অধীনে কিন্তু প্রত্যেকে স্বতন্ত্র সত্তা। একটি ম্যাক্রোস্টেটে যতগুলো আলাদা আলাদা মাইক্রোস্টেট থাকতে পারে তাদের সংখ্যাই হল মাল্টিপ্লিসিটি। সোজা কথায়, মাইক্রোস্টেটের সংখাই মাল্টিপ্লিসিটি। তাহলে, ১০ যোগফলের যে ম্যাক্রোস্টেট, তার মাল্টিপ্লিসিটি কত? উত্তর হবে ৩। যদি জিজ্ঞেস করি, কতটি আলাদা উপায়ে ৩ যোগফলের ম্যাক্রোস্টেট বানাতে পারব? উত্তরটা পেরে যাওয়া উচিত – ২ (এই প্রশ্নে প্রকারান্তে মাল্টিপ্লিসিটিই জানতে চাওয়া হয়েছে)
এখন আমরা এই জ্ঞানকে পুঁজি করেই শিফট করব গ্যাসের অণুভর্তি একটা পাত্রে। এই পাত্রটা আমাদের সিস্টেম এবং তার অণুগুলো আমাদের ঐ ছক্কার মত। ছক্কার পিঠে থাকা ফোঁটার সংখ্যা যেমন তাদের পরিচয় ছিল তেমনি ধরি এই অণুগুলোর পরিচয় তাদের গতিশক্তিতে। তাহলে সিস্টেমটা যত বেশি শক্তি ধারণ করে থাকবে, তার অণুগুলোও তেমন অসংখ্য উপায়ে নিজেদের মধ্যে গতিশক্তি বন্টন করার সুযোগ পাবে। ফলে আমরা নিঃসন্দেহে বলে দিতে পারি, বেশি শক্তিসম্পন্ন সিস্টেমের মাল্টিপ্লিসিটি বেশি হবে, আর কম শক্তির সিস্টেমের মাল্টিপ্লিসিটি হবে তুলনামূলক কম।
আদতে যখন আমরা কোনো সিস্টেমের তাপমাত্রা, চাপ, আয়তন উল্লেখ করি, তখন আমরা তার ম্যাক্রোস্টেট তুলে ধরি (বৃহৎ পরিসরে বলে দিতে চাই ঐ সিস্টেমের ধারণকৃত শক্তি কত, ঠিক যেন ছক্কাদ্বয়ের যোগফল উল্লেখ করার মত)। একটা নির্দিষ্ট ম্যাক্রোস্টেটসম্পন্ন সিস্টেমের শক্তি নির্দিষ্ট। 300 K, 1 atm ও 500 ml এর একটি সিস্টেম যে ম্যাক্রোস্টেটে আছে বা যে শক্তি ধারণ করছে; 300 K, 1.5 atm ও 600 ml এর সিস্টেম নিশ্চয়ই সেরকম শক্তিসম্পন্ন হবে না – তাই এটি অন্য একটি ম্যাক্রোস্টেট নির্দেশ করবে। আর যদি আমরা সিস্টেমের ভিতরে ঢুকে অণুগুলোর প্রত্যেকটির গতিশক্তির তালিকা করি তবে তা উল্লেখ করবে সিস্টেমটির মাইক্রোস্টেট। এ কথা বলা বাহুল্য যে, যেকোনো এক মুহূর্তে সিস্টেম যে মাইক্রোস্টেটে থাকবে পরমুহূর্তেই সেই মাইক্রোস্টেটে থাকবে না কারণ গতিশীল অণুগুলো পরস্পর সঙ্ঘর্ষে লিপ্ত হয়ে অন্যরকম গতিশক্তিসম্পন্ন হয়ে যাবে, যা ব্যাখা করতে দরকার পড়বে অন্য আরেকটি লিস্ট (সিস্টেমের মোট শক্তি কিন্তু অপরিবর্তীতই থাকবে, তার ম্যাক্রোস্টেটে কোনো চেঞ্জ আসবে না)। একটা সিস্টেম তাহলে আণবিক লেভেলে এরকম কত প্রকার সজ্জা নিতে পারে? মাল্টিপ্লিসিটি কোথায় কাজে লাগে তা এই প্রশ্নেই বুঝে ফেলার কথা।
মাল্টিপ্লিসিটির হিসাব কেবল গতিশক্তি সম্বন্ধীয় নয়, ত্রিমাত্রিক স্থানে অণুগুলোর অবস্থান বিবেচনা করেও মাল্টিপ্লিসিটি হিসাব করা হয়। আমরা আমাদের আলোচনার সুবিধার্থে কেবল অণুদের গতিশক্তিতেই সীমাবদ্ধ থেকেছি। এই যদি হয় অবস্থা, ভাবা যায় একটা গ্যাসভর্তি বেলুনের সম্ভাব্য মাইক্রোস্টেটের সংখ্যা কেমন অকল্পনীয় হতে পারে? (এসব হিসাব সম্পূর্ণই পরিসংখ্যানের দান, কোথাও উল্লেখ করেছিলাম না পরিসংখ্যানের কথা?)
সে সংখ্যা কল্পনা করা যাক বা না যাক, সিস্টেমে শক্তির আগমন কীভাবে তার অণুসমূহকে চঞ্চলতর করে মাল্টিপ্লিসিটি বাড়িয়ে দেয়, বাড়ায় বিশৃংখলা এটা বুঝলেই এনট্রপির সাথে বিশৃংখলার সম্পর্ক আবিষ্কারের চেষ্টায় আমরা কল্পনাতীত সফল বলে নিজেদের আপাতত দাবী করতেই পারি!
কেন?
কারণ বিশৃংখলার সাংখ্যিক প্রকাশ এই মাল্টিপ্লিসিটি নিয়েই যে এনট্রপির ক্যালকুলেশন করার আস্ত একটা সমীকরণ আছে! (চলবে)

কোপা শামশু, কোপা। 8|
baah 😛
😀 😛