আজকে আমরা আরেকটি প্রোগ্রামিং প্রবলেম নিয়ে আলোচনা করব । আমরা ইতোমধ্যে বিভিন্ন অনলাইন জাজ এর কিছু প্রবলেম নিয়ে আলোচনা করেছি । কম্পিউটার বিজ্ঞান এর একটি অত্যন্ত গুরুত্বপূর্ণ শাখা হচ্ছে প্রোগ্রামিং প্রবলেম সমাধান । এতে আমাদের চিন্তার দক্ষতা যেমন বাড়ে , ঠিক তেমনিভাবে আমাদের একাডেমিক এবং জ্ঞানের পরিধি ও বাড়াতে এটি খুবই সহায়ক ।
তো প্রবলেম পাওয়ার জন্য অসংখ্য সাইট বা অনলাইন জাজ রয়েছে । এর মধ্যে খুবই পরিচিত একটি সাইট Uva Online Judge. আজকে আমরা এই সাইটের একটি প্রবলেম নিয়ে আলোচনা করব । আবার এই প্রবলেমটি আরেকটি অতি পরিচিত এবং খুবই জনপ্রিয় আরেকটি অনলাইন জাজ Light Oj এও দেয়া আছে ।
তো আমরা আর কথা না বাড়িয়ে আমাদের আলোচনা শুরু করি ।
প্রবলেম লিঙ্কঃ https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=3835
http://lightoj.com/volume_showproblem.php?problem=1388&language=english&type=pdf
প্রবলেমটিতে বলা হয়েছে , আমাদের একটি ট্রাপিজিয়াম আঁকতে হবে ।যেখানে ট্রাপিজিয়াম এর বাহু AB এর A আর B এর কো-অর্ডিনেট দেয়া আছে । আর অবশিষ্ট ৩ বাহু b,c,d এর দৈর্ঘ্য দেয়া আছে । আমাদের প্রিন্ট করতে হবে C আর D পয়েন্ট এর কো-অর্ডিনেট । আর সবপয়েন্ট গুলো এমনভাবে আসতে হবে যাতে সেগুলো ঘড়ির কাঁটার বিপরীতদিকে বা anti – clockwise অবস্থান করে ।
Algorithm :
আমাদের মূল কাজ আসলে খুবই সোজা । আমরা এখানে প্রথমে একটি পয়েন্ট বের করব AB বাহুর অপর । মনে করি পয়েণ্টটি P . আমরা যদি CD এর সমান্তরাল করে AB এর একটি অংশ কেটে নিই তাহলে আমরা বলতে পারি AP = a – c আর PB = c । তাহলে আমরা এই হিসেবে P এর স্থানাংক পেয়ে যাবে । এখন আমরা DP = b বলতে পারি । আর আমরা জানি AD = d . তাহলে আমরা এখন এই দুইটি মানের অপর ভিত্তি করে সমীকরণ তৈরী করতে পারি । আর এই সমীকরণ সমাধান করে আমরা ২টি বিন্দু পাব । এর মধ্যে যে বিন্দুটি আমার AB সাপেক্ষে ঘড়ির কাঁটার বিপরীতে অবস্থান করবে সেটিই হবে আমার D এর নির্ণেয় স্থানাংক । ঠিক একই ভাবে আমরা C এর স্থানাংক বের করব ।
আমরা ব্যাপারটিকে একটু ছবিতে দেখাই
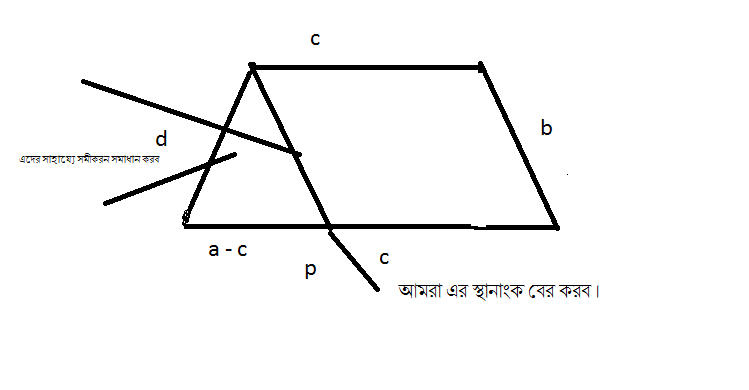
Equations :
- লাইন সমীকরণ : Ax + BY = C
- x এর মান বের করার সমীকরণ / দ্বিঘাত সমীকরণ : Dx^2 +Ex + F = 0 , (x = – E + sqrt(E^2 – 4 * D * F) ) / (2 * D) , (x = -E – sqrt(E^2 – 4 * D * F) ) / (2 * D) .
- আর area বের করার সমীকরণ , 0.5 * x1 * (y2 – y3) + x2 * (y3 – y1) + x3 8 (y1 – y2)
- A = 0 না লিখে আমরা ব্যবহার করব fabs(A) <= 1e-9
Code :
#include <bits/stdc++.h>
#define EPS 1e-9
using namespace std;
double distance(double x1, double y1, double x2,double y2) {
double value;
value = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
value = sqrt(value);
return value;
}
double find_point(double x1,double m,double x2, double n){
double value;
value = m * x2 + n * x1;
value = value / (m + n);
return value;
}
double tri_area(double x1,double y1,double x2,double y2,double x3,double y3) {
double value;
value = x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2);
return value;
}
void line_intersection(double xa,double ya, double d,double xp,double yp,double b,double arrx[5],double arry[5]) {
double A,B,C;
A = 2 * (xp - xa);
B = 2 * (yp - ya);
C = xa * xa - xp * xp + ya * ya - yp * yp + b * b - d * d;
double D,E,F,value;
double ansx1,ansx2,ansy1,ansy2;
if(fabs(A) <= EPS && B != 0) {
ansy1 = (- C * 1.0 / B);
ansy2 = ansy1;
value = d * d - (ansy1 - ya) * (ansy1 - ya);
value = sqrt(value);
ansx1 = xa + value;
ansx2 = xa - value;
}
else if(fabs(B) <= EPS && A != 0) {
ansx1 = (- C * 1.0) / A;
ansx2 = ansx1;
value = d * d - (ansx1 - xa) * (ansx1 - xa);
value = sqrt(value);
ansy1 = ya + value;
ansy2 = ya - value;
}
else {
D = A * A + B * B;
E = 2 * B * C + 2 * A * B * xa - 2 * A * A * ya;
F = C * C + A * A * xa * xa + 2 * C * A * xa + A * A * ya * ya - A * A * d * d;
value = E * E - 4.0 * D * F;
value = sqrt(value);
ansy1 = (- E + value) / (2.0 * D);
ansy2 = (- E - value) / (2.0 * D);
ansx1 = -(B * ansy1 + C) / A;
ansx2 = -(B * ansy2 + C) / A;
}
double area1,area2;
area1 = tri_area(xa,ya,xp,yp,ansx1,ansy1);
area2 = tri_area(xa,ya,xp,yp,ansx2,ansy2);
if(area1 > 0) {
arrx[0] = ansx1;
arry[0] = ansy1;
}
if(area2 > 0) {
arrx[0] = ansx2;
arry[0] = ansy2;
}
}
int main(void)
{
int T,t;
double xa,ya,xb,yb,xc,yc,xp,yp,xq,yq;
double a,b,c,d;
double area;
scanf("%d",&T);
for(t = 1; t <= T;t++) {
scanf("%lf %lf %lf %lf %lf %lf %lf",&xa,&ya,&xb,&yb,&b,&c,&d);
double darrx[5],darry[5],carrx[5],carry[5];
a = distance(xa,ya,xb,yb);
xp = find_point(xa,a-c,xb,c);
yp = find_point(ya,a-c,yb,c);
line_intersection(xa,ya,d,xp,yp,b,darrx,darry);
double xd = darrx[0];
double yd = darry[0];
xq = find_point(xa,c,xb,a-c);
yq = find_point(ya,c,yb,a-c);
line_intersection(xq,yq,d,xb,yb,b,carrx,carry);
double xc = carrx[0];
double yc = carry[0];
printf("Case %d:\n",t);
printf("%0.8lf %0.8lf %0.8lf %0.8lf\n",xc,yc,xd,yd);
}
return 0;
}
তো আজকের মত এখানেই বিদায় । সামনে ঈণ শা আল্লাহ আমরা আরো অনেক সুন্দর সুন্দর প্রবলেম নিয়ে আলোচনা করব ।
কৃতজ্ঞতা স্বীকার : ওয়াসিফ মোহাম্মদ ভাই ।
