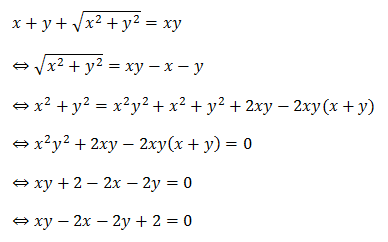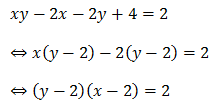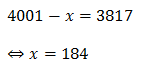কুইজ :: Nov 2015; Week 2

সমস্যা-1: এমন সব সমকোণী ত্রিভুজ বিবেচনা করা হচ্ছে যাদের সমকোণ সংলগ্ন বাহু দুটির মান ধনাত্মক পূর্ণসংখ্যা নির্দেশ করে। এরকম ত্রিভুজগুলোর মধ্যে কতগুলোর পরিসীমার মান ক্ষেত্রফলের দ্বিগুণ?

সমাধান: ধরি, সমকোণ সংলগ্ন বাহু দুটির একটি x এবং অপরটি y । তাহলে,

সুন্দর একটি সমীকরণ পাওয়া গেল অবশেষে। কিন্তু, সবচেয়ে আশ্চর্যজনক ব্যাপারটি হবে এখন। সমীকরণের দুইপাশে আমরা 2 যোগ করব।

এখানে, বুঝা যাচ্ছে যে x, y>2 ; কারণ, নইলে এর মান 2 হবে না। আবার x, y এর মান ঋণাত্মক হতে পারে না।

একটু সংখ্যা বসিয়ে দেখলেই x, y এর মান কি কি হতে পারে তা সম্পর্কে ধারণা পাব। x=4, y=3 হলে এর মান 2 হবে। আবার x=3, y=4 হলেও তা সম্ভব। কিন্তু, (4,3), (3,4) ছাড়া অন্য কোনো ধনাত্মক পূর্ণসংখ্যার জন্য সমীকরণটি সিদ্ধ হবে না।

আর তাই, কাঙ্ক্ষিত ত্রিভুজের সংখ্যা মাত্র একটি। এবং, শর্ত পূরণকারী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুটির একটিকে 3 একক এবং আরেকটিকে 4 একক হতে হবে।

সমস্যা-2: ধরি, Z={9^k | যখন, 0<=k<=4000}. যদি 9^4000 সংখ্যাটি 3817 টি অংক দ্বারা গঠিত হয় এবং এর সর্ববামের সংখ্যাটি 9 হয় তাহলে Z সেটটিতে 9 দিয়ে শুরু হওয়া কতগুলো সংখ্যা থাকবে?

সমাধান: 9^k-1 এর চেয়ে 9^k এর ডিজিট সংখ্যা এক বেশি, শুধুমাত্র সেইসব ক্ষেত্র বাদে যেখানে 9^k সংখ্যাটি 9 দিয়ে শুরু হয়। এই ব্যতিক্রমী কেসে 9^k-1 সংখ্যাটি 1 দিয়ে শুরু হবে। এছাড়া অন্য সব ক্ষেত্রে 9 এর ঘাত বাড়লে ডিজিটও একটি বাড়ে। এই হিসাব অনুযায়ী 9⁴⁰⁰⁰ সংখ্যাটিতে ডিজিট থাকবে [4001-(যতগুলো সংখ্যা 9 দিয়ে শুরু)] । মনে করি, x সংখ্যক সংখ্যা আছে যেগুলো 9 দিয়ে শুরু হয়। ফলে,

অর্থাৎ, Z সেটটির 184 টি সংখ্যা 9 দিয়ে শুরু হবে।

সমস্যা-3: 10 টি কুকুর 7 টি বিস্কুটের সন্ধান পেল। কতভাবে তারা বিস্কুটগুলো খেতে পারে? (কুকুররা বিস্কুট শেয়ার করে না! আর বিস্কুটগুলো দেখতে এক রকম হলেও কুকুরগুলো কিন্তু নয়।)

সমাধান: যদি বিস্কুটগুলো ভিন্ন রকম হত তাহলে হিসাবটা সহজ হত। সেক্ষেত্রে, 10⁷ হত উত্তর। কিন্তু, বিস্কুটগুলো Identical হওয়ায় হিসাবটা একটু অন্যরকম হবে।

এখানে, এমন কোনো শর্ত নেই যে প্রত্যেক কুকুরকে একটি করে বিস্কুট পেতে হবে। (যা আসলে সম্ভবও নয়!) আমরা যা করব তা হচ্ছে 7 টি বিস্কুটের সাথে আরো 10 টি বিস্কুট মিশাব। এবং সাথে আরেকটি শর্ত জুড়ে দিব। শর্তটা হচ্ছে প্রত্যেকটি কুকুর কমপক্ষে একটি বিস্কুট পাবে। বন্টনকাজ শেষ হলে আমরা আরেকটি কাজ করব। সেটা হচ্ছে প্রত্যেকটি কুকুরের কাছ থেকে একটি বিস্কুট নিয়ে নিব। ফলে, আসল ঘটনার কোনো হেরফের হচ্ছে না। কিন্তু, আমাদের হিসাবের ক্ষেত্রে তা অনেক সুবিধা করে দিবে।

এখন বিস্কুট দাঁড়াল 17 টি। এবার আমরা এগুলোকে পাশাপাশি রাখব। আমাদের এই বিস্কুটগুলোকে 10 ভাগে ভাগ করতে হবে। 17 টি বিস্কুটের মাঝে জায়গা আছে 16 টি। এই 16 টি জায়গার মধ্যে 9 টি জায়গাকে চিহ্নিত করলেই 10 টি কুকুরের জন্য বিস্কুট বণ্টিত হয়ে যায়। ফলে, উপায় সংখ্যা হচ্ছে অথবা 11440 টি।