বর্গমূল নির্ণয়
আমরা ছোটবেলায় কোনো একটা সংখ্যার বর্গমূল কিভাবে বের করতে হয় তার একটি সহজ ও কার্যকর উপায় শিখেছিলাম। আমাদের অনেকের মনেই হয়ত প্রশ্ন জাগত, উপায়টা কিভাবে কাজ করে। আজ এ পর্বে আমরা সেই ব্যাপারটা নিয়েই খানিকটা আলোচনা করব।
ধরি, আমরা 213 এর বর্গমূল নির্ণয় করতে চাই।
আমরা প্রথমে দেখতাম 2 এর চেয়ে ছোট বর্গ সংখ্যাটি কত এরপর 13 কে জোড়া ধরে নামিয়ে দিতাম (যেখানে সাধারণ ভাগে কেবল একটা সংখ্যা নামাই 😀 ) মানে
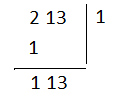
এবার আমরা 1 কে দ্বিগুণ করে দিয়ে এমন একটি সংখ্যা (এখানে 4) নিতাম যাতে ঐ সংখ্যা ও দ্বিগুণ করে পাওয়া সংখ্যা (এখানে, 24) গুণ করলে 113 এর মধ্যে দিয়ে দেয়া যায়
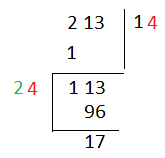
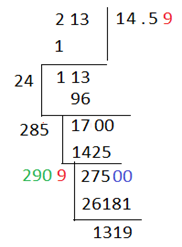
আবার অনেকেই হয়ত একবারে ভাবতাম 213 এর চেয়ে ছোট সবচেয়ে কাছের বর্গ সংখ্যাটা কত (এখানে 14)।
এরপর আমরা দশমিক দিয়ে জোড়া ধরে শুন্য নিয়ে আসতাম আর আমাদের ভাগফলে ততক্ষণ পর্যন্ত আসা সংখ্যাকে দ্বিগুণ করে দিয়ে একই প্রক্রিয়া বারবার চালিয়ে আমাদের আনুমানিক ঘর পর্যন্ত বর্গমূল বের করে ফেলতাম
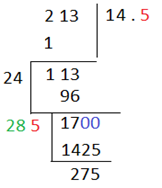
এভাবে আমরা যত ঘর পর্যন্ত ইচ্ছা তত ঘর পর্যন্ত বের করে ফেলতে পারি।
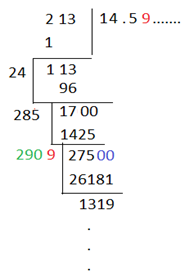
আচ্ছা এইবার আসা যাক এই উপায়টা কিভাবে কাজ করে, কেনোইবা আমরা এইভাবে বিদঘুটে ভাগ করে দিব্যি সঠিক বর্গমূলটা পেয়ে যাচ্ছি। :/
আমরা প্রথমে দেখছিলাম
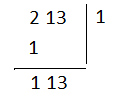
এর অর্থ আর কিছুই নয় আমরা খুজছিলাম 100 বা 102 এর কত গুণিতক যা একটি বর্গসংখ্যা তা দিয়ে 213 কে ভাগ করা যায় অর্থাৎ আমরা এভাবে 213 কে ভাবছিলাম
213 = 102 + 113
অর্থাৎ আমরা আমাদের প্রথম অনুমানটা করছিলাম যে 213 এর বর্গমূল 10 এর চেয়ে বড় কিছু একটা হবে।এবার আমরা আমাদের অনুমানটাকে আরও কাছে নিয়ে যাওয়ার চেষ্টা করব।
এরপর আমরা যে কাজটা করেছিলাম,

1 কে দ্বিগুণ করে 2 বানিয়েছিলাম অর্থাৎ যেহেতু 1 দশকের স্থানের অংক তাই আমরা আসলে 10 কে দ্বিগুণ করে 20 বানিয়েছি। এরপর এই 20 এর সাথে একটা এক অঙ্কের সংখ্যা 4 যোগ করে তা দিয়ে গুণ করেছি (20 + 4) × 4 = 96 । এখন, প্রশ্ন হল কেনোই বা দ্বিগুণ করলাম আর কেনই বা নতুন একটা অংক বসিয়ে গুণ করলাম?
আচ্ছা, আমাদের প্রথম অনুমান ছিল 10 যা খুব একটা ভালো অনুমান ছিল না, তাই আমরা আমাদের অনুমানটাকে আরেকটু কাছাকাছি আনতে চাচ্ছিলাম এবং আমরা বুঝতে পারছিলাম আমাদের অনুমানটাকে আরও বাড়াতে হবে মানে তা 10 থেকে বড় কিছু একটা হবে।
213 = (102 + 2.10.1 + 12) + 92
আরেকটু এগিয়ে চেষ্টা করে দেখা যাক।
213 = (102 + 2.10.2 + 22) + 69
213 = (102 + 2.10.3 + 32) + 44
213 = (102 + 2.10.4 + 42) + 17
আর আগানো যাবে না, কারণ এরপর ই আসবে 152 মানে 225 যা 213 থেকে বড়। দ্বিগুণ করার ও নতুন অংক বসিয়ে গুণ করার কারণটা আশা করি ধরতে পেরেছো।
আমরা যা করছিলাম তা হল (2 × 10 + 1) × 1 = 2 × 10 × 1 + 12 মানে
(2 × 10 + 4) × 4 = 2 × 10 × 4 + 42 এই কারণেই ( (a+b)2 এর 2ab + b2 আকারের অংশটুকু তৈরী করার জন্যই) আমরা মূলত দ্বিগুণ করে একটা অংক বসিয়ে ঐ অংক দিয়েই আবার গুণ করেছিলাম। 😀
এইবার আমাদের অনুমান গিয়ে দাঁড়াল 14 তে,
213 = 142 + 17
মানে 213 এর বর্গমূল 14 এর থেকে বড় কিছু একটা হবে।
এবার আমাদের অনুমানকে আরও কাছাকাছি নিয়ে যাবার পালা। এরপর আমরা যে কাজটা করেছিলাম তা হলঃ

আচ্ছা, এখন একটু ভিন্নভাবে ভাবি, সাময়িক এর জন্যে ধরে নেই আমদের 21300 এর বর্গমূল বের করতে হবে মানে আমরা আমাদের শেষ সমীকরণটাকে 100 দিয়ে গুণ করে দিচ্ছি (কারণ 100 দিয়ে গুণ না করে 10 দিয়ে গুণ করলে পূর্ণবর্গ অংশটা পূর্ণবর্গ থাকবে না)।
21300 = 1402 + 1700
একইভাবে আগের মত, 2 x 140 × 5 + 52
বা, (2 x 140 + 5) × 5 বা, (280+5) × 5 বা, 285 × 5 = 1425
তার মানে,
21300 = 1402 + 1425 + 275
বা, 21300 = (1402 + 2 × 140 × 5 + 52) + 275
বা, 21300 = (140 + 5)2 + 275
বা, 21300 = (145)2 + 275
কিন্তু আমাদের তো 213 এর বর্গমূল বের করতে বলেছিল। তাহলে? আসলে আর কিছুই নয় আমরা এবার শেষ সমীকরণটাকে 100 দিয়ে ভাগ দিলেই তো হল। 😀
213.00 = (14.5)2 + 2.75
মানে 213 = (14.5)2 + 2.75
আমরা এবার আগের চেয়ে আরও ভালো অনুমান করেছি। 213 এর বর্গমূল 14.5 থেকে বড় কিছু একটা।
এবার আমাদের অনুমানকে আরও কাছাকাছি নিয়ে যাব। এরপর আমরা যে কাজটা করেছিলাম তা হলঃ
আচ্ছা, এবার সাময়িক এর জন্যে ধরে নেই আমদের 2130000 এর বর্গমূল বের করতে হবে মানে আমরা আমাদের শেষ সমীকরণটাকে 10000 দিয়ে গুণ করে দিচ্ছি।
একইভাবে আগের মত, 2 × 1450 x 9 + 92
বা, (2 × 1450 + 9) × 9 বা, (2900+9) × 9 বা, 2909 × 9 = 26181
তার মানে,
2130000 = 14502 + 27500
বা, 2130000 = 14502 + 2 × 1450 × 9 + 92 + 1319
বা, 2130000 = (1450 + 9)2 + 1319
বা, 2130000 = (1459)2 + 1319
এবার শেষ সমীকরণটাকে 10000 দিয়ে ভাগ দেই,
213.0000 = (14.59)2 + 0.1319
বা, 213 = (14.59)2 + 0.1319
আমরা এবার আগের চেয়ে আরও ভালো অনুমান করেছি। 213 এর বর্গমূল 14.59 থেকে বড় কিছু একটা।
আমরা দশমিকের পর দুই ঘর পর্যন্ত 213 এর বর্গমূল শুদ্ধভাবে নির্ণয় করে ফেলেছি।
এই একই প্রক্রিয়া বার বার চালিয়েই আমরা আসলে বর্গমূল নির্ণয় করি, আমরা এভাবে যতবার এই একই প্রক্রিয়ার পুনরাবৃত্তি করতে থাকব ততই আমরা আমদের অনুমানকে কোনো সংখ্যা এর বর্গমূলের প্রকৃত মানের কাছাকাছি নিয়ে যেতে পারব। 🙂
ঘনমূল নির্ণয়
এখন আমরা দেখবো কিভাবে আমরা বর্গমূলের মত হাতে হাতেই ঘনমূল বের করে ফেলতে পারি।
ধরি, আমরা 2877 এর ঘনমূল বের করতে চাই। কাজটা অবশ্যই বর্গমূল বের করার মত অতটা সহজ হবে না কিন্তু অনেকটা বর্গমূল নির্ণয় করার মত করেই আমরা এগিয়ে যাব।
আমরা প্রথমে আগের মতই দেখব 2 এর চেয়ে ছোট ঘন সংখ্যাটি কত এরপর 877 কে ধরে নামিয়ে দিব। মানে,
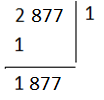
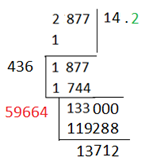
এবার একটু লক্ষ্য করো। এবার ভাগফলে যা আছে (মানে 1) তাকে বর্গ করে 3 দিয়ে গুণ করব। একে পাশে লিখে রাখি। এইবার আমরা ভাগফলের সংখ্যাটিকে 3 দিয়ে গুণ করব এবং যেই এক অংকের সংখ্যাটাকে অনুমান করে নিব তাকে এর সাথে গুণ করব। গুণফল সংখ্যাটির একক স্থানীয় অংককে এক ঘর ডানে সরিয়ে উল্টোদিক থেকে আগের সংখ্যার ঠিক নিচ বরাবর বসিয়ে ঐ রাখা সংখ্যার সাথে যোগ করে দিব। এবার ২য় বারে পাওয়া সংখ্যাটিকে পাশে রাখি। এরপর অনুমানের সংখ্যাটাকে বর্গ করি। বর্গ সংখ্যাটির একক স্থানীয় অংককে ঠিক আগের এক ঘর ডানে সরিয়ে উল্টোদিক থেকে আগের সংখ্যার ঠিক নিচ বরাবর বসিয়ে ২য় বারে পাশে রাখা সংখ্যার সাথে যোগ করে দিব। সবশেষে অনুমান করা সংখ্যাটির সাথে প্রাপ্ত সংখ্যাটি গুণ করে দিব। (কি বুঝতে অসুবিধা হল? 😀 নিচের ছবিটা দেখো তাহলেই বুঝতে পারবে।)
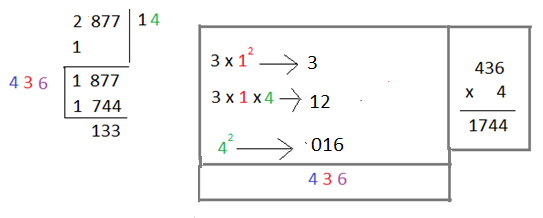
এবার আমরা যে কাজটি করব তা হলো বর্গমূলের ক্ষেত্রে আমরা দশমিক দিয়ে ২ টি শুন্য নামাতাম এক্ষেত্রে আমরা ৩ টি শুন্য নামাব। এরপর একই কাজের পুনরাবৃত্তি ঘটাব। তার মানে,
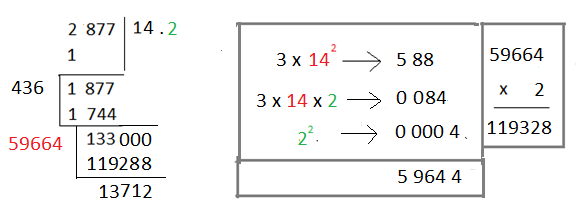
আমরা দুই ঘর পর্যন্ত ঘনমূল বের করে ফেলেছি। 😀 এভাবে একই প্রক্রিয়ার পুনরাবৃত্তি করে আমরা যত ঘর পর্যন্ত ইচ্ছা তত ঘর পর্যন্ত ঘনমূল বের করতে পারি।

এবার তো আমরা আগের বর্গমূলের উপায়ের চেয়ে আরও বিদঘুটে রাস্তা অবলম্বন করেছি। আচ্ছা, দেখা যাক কেন আমাদের এই উপায় কাজ করে। 😀
আমরা প্রথমে দেখছিলাম
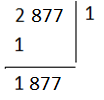
এর অর্থ আর কিছুই নয় আমরা খুজছিলাম 1000 বা 103 এর কত গুণিতক যা একটি ঘনসংখ্যা তা দিয়ে 2877 কে ভাগ করা যায় অর্থাৎ আমরা এভাবে 2877 কে ভাবছিলাম
2877 = 103 + 1877
অর্থাৎ আমরা আমাদের প্রথম অনুমানটা করছিলাম যে 2877 এর ঘনমূল 10 এর চেয়ে বড় কিছু একটা হবে।এরপর আমরা আমাদের অনুমানটাকে আরও কাছে নিয়ে যাওয়ার চেষ্টা করেছি।
এরপর আমরা যে কাজটা করেছিলাম,
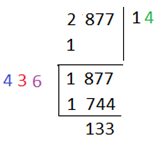
তোমরা যদি বর্গমূলের ব্যাপারটা বুঝে থাক তাহলে আশা করি বুঝে গেছো কেনো আমরা তিন ঘর করে নামাচ্ছিলাম। 😀
এবার কথা হল 436 পেতে আমরা ঐ পথ কেনো বেছে নিলাম?
আমাদের প্রথম অনুমান ছিল 10 যা খুব একটা ভালো অনুমান ছিল না, তাই আমরা আমাদের অনুমানটাকে আরেকটু কাছাকাছি আনতে চাচ্ছিলাম এবং আমরা বুঝতে পারছিলাম আমাদের অনুমানটাকে আরও বাড়াতে হবে মানে তা 10 থেকে বড় কিছু একটা হবে।
2877 = (103 + 3.102.1 + 3.10.12 + 13) + 1545
আরেকটু এগিয়ে চেষ্টা করে দেখা যাক।
2877 = (103 + 3.102.2 + 3.10.22 + 23) + 1149
2877 = (103 + 3.102.3 + 3.10.32 + 33) + 680
2877 = (103 + 3.102.4 + 3.10.42 + 43) + 133
আর আগানো যাবে না, কারণ এরপর ই আসবে 153 মানে 3375 যা 2877 থেকে বড়।
আমরা আসলে এই কাজটিই করছিলাম এভাবে (3.102 + 3.10.4 + 42) × 4 ।
আমরা যে 1 পেয়েছি তা আমাদের ঘনমূলের দশক স্থানীয় অংক মানে 10। এখন প্রথমটি এর সাথে যেহেতু 102 বা 100 গুণাকারে আছে তাই গুণফলটি অবশ্যই দুই ঘর বামে সরে যাবে অর্থাৎ শেষে ২টি শুন্য হবে এবং দ্বিতীয়টি এর সাথে যেহেতু 10 গুণাকারে আছে তাই গুণফলটি অবশ্যই এক ঘর বামে সরে যাবে অর্থাৎ শেষে ১টি শুন্য হবে আর শেষটির সাথে যেহেতু কোন 10 গুণাকারে নেই তাই এর শেষে অবস্থানের জন্য কোন শুন্য হবে না। আমরা এই ব্যাপারটাকেই উল্টোভাবে বলেছি যে, প্রথমটি থেকে দ্বিতীয়টি এক ঘর ডানে আর দ্বিতীয়টি থেকে তৃতীয়টি আরও এক ঘর ডানে সরে যাবে।
আসলে ঘটনা যা ঘটেছে তা হলঃ
3 x 102 = 300
3 x 10 x 4 = 120
42 = 16
(3.102 + 3.10.4 + 42) = 436
_ × 4
(3.102 + 3.10.4 + 42) × 4 = 1744
এই কারণেই ( (a+b)3 এর 3a2b + 3ab2 + b3 আকারের অংশটুকু তৈরী করার জন্যই) আমরা মূলত এইভাবে 436 হিসেব করে তারপর গুণ করেছিলাম। 😀
এইবার আমাদের অনুমান গিয়ে দাঁড়াল 14 তে,
2877 = 143 + 133
মানে 2877 এর ঘনমূল 14 এর থেকে বড় কিছু একটা হবে।
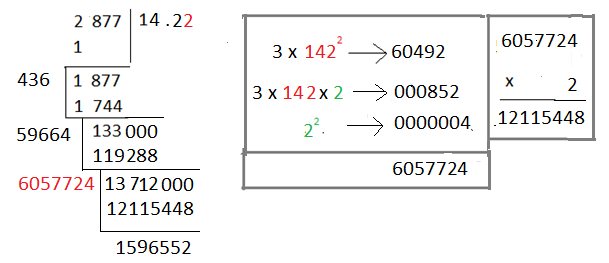
এরপর একইভাবে বর্গমূল বের করার উপায়ের মত, ঘনমূল বের করার ক্ষেত্রে আমাদের অনুমানকে সত্যিকার ঘনমূলের আরও কাছাকাছি নিয়ে যাওয়ার জন্যে আমরা সাময়িক এর জন্য ধরে নিয়েছি আমরা 2877000 এর ঘনমূল নির্ণয় করছি (মানে এইবার আমরা আমাদের শেষ সমীকরণকে 1000 দিয়ে গুণ করেছি)।
2877000 = 1403 + 133000
এরপর একইভাবে আগের মত করে,
2877000 = (1403 + 3 × 1402 × 2 + 3 × 140 × 22 + 23 ) + 13712
বা, 2877000 = (140 + 2)3 + 13712
বা, 2877000 = 1423 + 13712
এবার দিয়ে ভাগ করলে দাঁড়ায়,
2877.000 = 14.23 + 13.712
বা, 2877 = 14.23 + 13.712
এরপর বর্গমূলের মত একইভাবে এই প্রক্রিয়া বারবার চালিয়ে আমরা ঘনমূল বের করে ফেলতে পারি।
এইভাবে আমরা আমাদের যত ঘর পর্যন্ত ইচ্ছা তত ঘর পর্যন্ত ঘনমূল বের করতে পারি। 😀
আশা করি, বর্গমূল আর ঘনমূল বের করার উপায়গুলো কেন কাজ করে তা বুঝতে পেরেছো। আজ তাহলে এ পর্যন্তই। 😀

Josh
অনেক ভালো লাগলো কিন্তু দুই এর বর্গমূল কিভাবে করতে হয় যদি একটু দেখিয়ে দিতেন ???