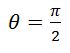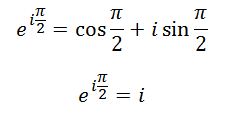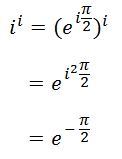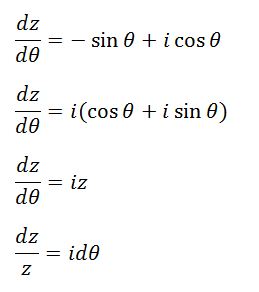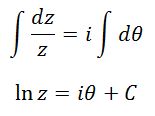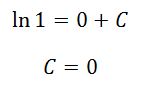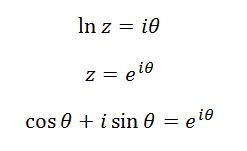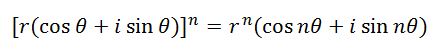কুইজ :: Oct 2015; Week 2

সমস্যা-1: একটি নক আউট টুর্নামেন্টে n জন অংশগ্রহণ করেছে। নিয়ম হচ্ছে, কোনো একটি ম্যাচে যে হারবে সে টুর্নামেন্ট থেকে বাদ পড়বে। তাহলে, একজন বিজয়ী পাওয়ার জন্য টুর্নামেন্টটিতে কতগুলো ম্যাচের আয়োজন করতে হবে?

সমাধান: অনেকেই হয়তো টুর্নামেন্টটিকে অনেকগুলো রাউন্ডে বিভক্ত চিন্তা করে সমস্যাটির সমাধানের চেষ্টা করবে! তারপর n সংখ্যাটি 2 এর গুণিতক কিনা তা নিয়ে দ্বিধায় পড়ে যাবে! যারা সমস্যাটির সমাধান করতে পেরেছ তাদের অভিনন্দন। আর যারা পার নি তারা নিচের কয়েকটি লাইন পড়।

সহজ একটা কথার উত্তর চাই! একটা ম্যাচে কয়জন প্রতিদ্বন্দ্বী বাদ পড়তে পারে? উত্তর, একজন। আমরা যদি n জন অংশগ্রহণকারী থেকে 1 জন বিজয়ী পেতে চাই তাহলে টুর্নামেন্ট থেকে কতজনকে বাদ দিতে হবে? উত্তর, (n−1) জন। একটা ম্যাচে বাদ পড়ে 1 জন; তাহলে (n−1) জন বাদ পড়বে (n−1) সংখ্যক ম্যাচে। এটাই আমাদের কাঙ্ক্ষিত সমাধান।

সমস্যা-2:  এর মান কত? 

সমাধান: প্রথমেই আমাদের জেনে নিতে হবে Euler’s formula। আমি এখন শুধু Euler’s formula উদ্ধৃত করব এখানে। (প্রমাণ দেয়া আছে সবগুলো সমস্যার সমাধানের পর)

উপরের সমীকরণটিতে  বসাও,

তার মানে,

সমস্যা-3:

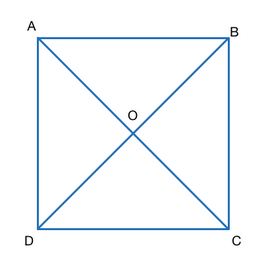
ABCD একটি বর্গ। A, B, C, D ও O – এই 5 টি বিন্দুর মধ্য থেকে যেকোনো 3 টি নিয়ে কতগুলো সমকোণী ত্রিভুজ বানানো সম্ভব?

সমাধান:

এখানে, প্রদত্ত 5 টি বিন্দু থেকে যেকোনো 3 টি বেছে নিয়ে সমকোণী ত্রিভুজ গঠন করতে হবে।

এই কাজটি করা সম্ভব  বা 10 উপায়ে। কিন্তু, এই 10 উপায়ের দুইটিতে আমরা কোনো সমকোণী ত্রিভুজ পাব না। এই দুটি উপায় হল A, O, C এবং B, O, D ।

সুতরাং, শর্ত মেনে গঠনকৃত মোট সমকোণি ত্রিভুজের সংখ্যা দাঁড়াবে 8 টি।

Euler’s formula::

এই ফর্মুলাটি হচ্ছে,

এই অংশে আমরা Euler’s formula প্রমাণ করার চেষ্টা করব। প্রথমেই ধরি,

Θ এর সাপেক্ষে উপরের সমীকরণটিকে অন্তরীকরণ বা Differentiate করলে পাব,

এখন, সমীকরণটিকে আমরা যোগজীকরণ বা Integrate করব।

C এর মান আমাদের জানতে হবে।

সমীকরণটিতে θ=0 বসালে z=1 পাওয়া যায়। ফলে,

আর তাই,

De Moivre’s theorem টিও Euler’s formula থেকে প্রমাণ করা সম্ভব। De Moivre’s theorem টি হল,

এটা নিজ গরযে প্রমাণ করে নিও!

আর হ্যাঁ, ফিচারড ইমেজে যে ইকুয়েশনটা আছে তাও Euler’s formula থেকে বের করার চেষ্টা কর। 😀