এ পর্বের শুরুতে আমরা Rearrangements ও Derangements নিয়ে কথা বলব। প্রথমেই সংজ্ঞা দিয়েই শুরু করি-
Rearrangement:: কোনো string, word বা sequence এর উপাদানসমূহের যেকোনো ধরনের বিন্যাসকেই Rearrangement বলে। (মূল যে বিন্যাস থাকে সেটাও একটা rearrangement) মানে, নির্দিষ্ট সংখ্যক উপাদানকে আমরা ভিন্ন ভিন্ন ভাবে সাজিয়ে যতগুলো word বা sequence তৈরি করতে পারি সবগুলোই একেকটি rearrangement । এর আগে আমরা যেসব permutation নিয়ে কাজ করেছি সেগুলোতে আমরা আসলে ‘rearrangement কতগুলো’ সেটা খুঁজে বের করেছি কেবল।
Derangement:: Derangement হচ্ছে এমন ধরণের rearrangement যেখানে কোনো উপাদানই তার আসল/মূল জায়গায় অবস্থান করে না। অর্থাৎ, মূল বিন্যাসে উপাদানগুলো যেসব জায়গায় ছিল সেসব জায়গায় উপাদানগুলো আর না বসিয়ে আমরা যে rearrangement গুলো পাব সেগুলোই derangement ।
উদাহরণ দেয়া যাক তবে! ‘ABC’ –এই string নিয়ে চিন্তা করি। এর কতগুলো rearrangement সম্ভব? Permutation দিয়ে সহজেই সবাই বের করে ফেলতে পারি এ প্রশ্নের উত্তর। ‘ABC’ string টির 3! বা 6 টি rearrangement সম্ভব। এখন প্রশ্ন আসল, derangement কয়টি? এটা বের করার জন্য এখনো আমরা কোনো কংক্রিট নিয়ম শিখিনি। তবে, সামান্য মাথা খাটালেই আমরা ‘ABC’ এর derangements গুলো বের করে ফেলতে পারব। ‘BCA’, ‘CAB’- এ দুটো derangement ই আছে। কারণ, ‘ABC’ মূল বিন্যাস হওয়ায় derangements এ প্রথম ঘরে A বসতে পারবে না। তাহলে, অপশন থাকল দুটো। হয় B অথবা C বসাতে হবে প্রথম ঘরে। ধরা যাক B বসিয়েছি প্রথম ঘরে। তাহলে, এখন অবশ্যই দ্বিতীয় ঘরে C বসাতে হবে কেননা C কে তার মূল স্থান বা তৃতীয় ঘরে বসানো যাবে না। আর A বসবে তৃতীয় ঘরে। Derangement টি তাই দাঁড়াবে ‘BCA’। আমাদের হাতে আরেকটা অপশন ছিল। সেটা হচ্ছে প্রথম ঘরে C বসানো। এটা করলে B কে অবশ্যই তৃতীয় ঘরে বসাতে হবে আর A কে দ্বিতীয় ঘরে। ফলে, এক্ষেত্রে derangement টি হবে ‘CAB’। ‘ABC’ string টি ছোট বিধায় derangements কম। বেশি উপাদানের string এ আমরা অনেক derangements খুঁজে পাব। বড় string এর derangements কিভাবে গুণতে হয় তার কাঠকোট্টা নিয়ম আমরা এ সিরিজের পরবর্তী কোনো পর্বে শিখব।
Derangement এর আরেকটা উদাহরণ দেই। 15896 সংখ্যাটির একটি derangement হল 69581 । কারণ, এক্ষেত্রে কোনো উপাদানই তার মূল অবস্থানে বসছে না। এখন, একটা notation শিখে ফেলব। যদি আমাদের কাছে n distinct উপাদানের (মানে, সব উপাদান ভিন্ন) কোনো string, word বা sequence থাকে তবে তার মোট derangements এর সংখ্যা বুঝানোর জন্য আমরা Dn চিহ্নটি ব্যবহার করব। আগের প্যারায় দেখানো উদাহরণে D3=2 ছিল।
এখন একটা কাজ দেই! D1, D2, D4 -এ তিনটির মান খুঁজে বের কর।
Rearrangements and Derangements এর পর এখন আমরা Combinatorics এর আরেকটা অনেক গুরুত্বপূর্ণ ব্যবহার শিখব। আমি আশা করি তোমরা সবাই Prime Factorization সম্পর্কে জান অথবা কমপক্ষে শব্দ দুটি একত্রে শুনেছ এর আগে। যারা শুননি তাদের হতাশ হওয়ার কিছু নেই। আমি সংক্ষেপে এটি ব্যাখ্যা করছি।
“সব integer (পূর্ণ সংখ্যা) কে শুধুমাত্র prime numbers (মৌলিক সংখ্যা) এর গুণফল আকারে লেখা যায়।”
Prime number বলতে আমরা সেসব সংখ্যাগুলোকে বুঝি যেগুলো শুধুমাত্র 1 এবং সেই সংখ্যাটি দ্বারা বিভাজ্য। তার মানে যদি n সংখ্যাটি prime না হয় তাহলে n নিশ্চয়ই 1 এবং n ছাড়াও অন্য কোনো সংখ্যা দ্বারা বিভাজ্য হবে। অন্য যে সংখ্যাটি দ্বারা n বিভাজ্য হচ্ছে সে সংখ্যাটির ক্ষেত্রেও একই কথা প্রযোজ্য। এভাবে বিভাজ্যতার হিসাব করতে করতে আমরা এমন সংখ্যায় পৌঁছে যাব যা মৌলিক। মানে এটাকে আর ভাঙ্গানো যাচ্ছে না। ব্যাপারটা অনেকটা অণু-পরমাণু সংক্রান্ত কথা বার্তার মত। আমরা যেকোনো বস্তুকে অনেক ক্ষুদ্র ক্ষুদ্র অংশে বিভাজ্য হিসেবে চিন্তা করি। অণু পর্যন্ত গিয়ে আমরা থেমে যাই। কারণ অণু ভাঙলে আর বস্তুটির অস্তিত্বই থাকে না। অবশ্য মৌলের ক্ষেত্রে অন্য কথা! কারণ তখন পরমাণু পর্যন্ত ভাংলেও বস্তুটি স্বীয় ধর্মে ও কর্মে অস্তিত্বশীল থাকতে পারে। Prime Factorization ব্যাপারটাও আসলে একই। আমরা আমাদের চেনা পরিচিত সব সংখ্যাকে কিছু building blocks দিয়ে গঠিত চিন্তা করতে পারি যেখানে prime number গুলোই হচ্ছে building blocks!
উপরের প্যারাতে Prime Factorization যে থাকা সম্ভব ও থাকা উচিত সেটাই আমি প্রমাণ করেছি। এ নিয়ে আরো ঘাঁটতে পার। তবে আমার পথ এখন অন্য দিকে মোড় নিবে। 😀
ধরা যাক, n সংখ্যাটিকে আমরা prime numbers এ বিভক্ত করেছি। এবং, যা পেয়েছি তা হল-
এখন n এর যেসব divisor আছে তাদেরকেও কিন্তু prime numbers এ factored করা যায়। এবং, তাদের সাধারণ রূপ হবে,
যেখানে i তম prime number Pi এর ঘাত হবে bi এবং bi এর মান হতে পারে 0 থেকে ai পর্যন্ত যেকোনো integer । কেনো এটা সত্যি? কারণ যে সংখ্যাটি দিয়ে n কে ভাগ করা যাবে সে সংখ্যাটির Prime Factorization এ এমন কিছু থাকা যাবে না যা ভাগের পরও অবশিষ্ট থাকে। উদাহরণ দিচ্ছি, ব্যাপারটা পরিষ্কার হবে।
উপরে যা লিখেছি তা 6 এর Prime Factorization । 6 এর যেসব divisor আছে সেগুলো হল 1, 2, 3, 6 । এখন এদের Prime Factorization দেখা যাক।
আচ্ছা তার মানে, যেসব divisor আছে তাদের Prime Factorization এ কোনো prime number এর ঘাত হতে পারে 0 থেকে মূল সংখ্যাটির Prime Factorization এ ঐ একই prime number এর যে ঘাত ছিল সে সংখ্যা পর্যন্ত। তার মানে কোনো সংখ্যার Prime Factorization জানা থাকলে তার divisor গুলোর Prime Factorization কি হতে পারে তাও আমাদের জানা হয়ে যায়।
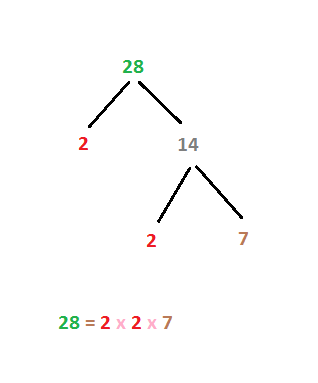
যেমন, ধরা যাক আমরা 28 সংখ্যাটির divisor গুলো কি কি তা আমরা জানতে চাই। প্রথমেই তাহলে 28 এর Prime Factorization জানতে হয়।
আচ্ছা, এখন কি শুধু উপরের সমীকরণ দেখেই বলে দিতে পারবে 28 এর divisor কয়টা? প্রথমে কিছুক্ষণ চেষ্টা কর। পারা উচিত। কমপক্ষে আধাঘণ্টা চেষ্টার পরও না পারলে এবার বাকি আর্টিকেল পড়।
আমরা আগেই দেখেছি যে divisor গুলোর Prime Factorization কি হতে পারে তা আমরা বলে দিতে পারি মূল সংখ্যাটির Prime Factorization দেখে। 28 এর যেকোনো divisor এর ক্ষেত্রেই Prime Factorization নিম্নরূপ হতে পারে।
এখানে divisor গুলোর সাধারণ একটি নাম m দিয়েছি। আচ্ছা, সমীকরণটিতে b1 ও b2 এর মান কত হতে পারে? b1 এর মান হতে পারে 0, 1 অথবা 2 আর b2 এর মান হতে পারে 0, 1 । তার মানে, divisor নির্ণয়ের ক্ষেত্রে b1 এর মানের জন্য 3 টি উপায় ও b2 এর মানের জন্য 2 টি উপায় আছে। তার মানে মোট 3×2=6 টি উপায় আছে। এখন 28 এর divisor গুলো একটু দেখি!
বুঝাই যাচ্ছে আমরা একটা সাধারণ ফর্মুলা পেয়ে গেছি। এই সাধারণ ফর্মুলাকে একটু গণিতের ভাষায় লেখি।
হলে n এর divisor পাওয়া যাবে (a1+1)(a2+1)…(an+1) টি। [মনে কর, a1 এর মান 2 । তাহলে divisor এর Prime Factorization এ P1 এর ঘাত হতে পারে 0, 1, 2 । তাহলে উপায় দাঁড়াল 3 বা (2+1)]
এখন উপরের ফর্মুলা ব্যবহার করে ‘88’, ‘900’ ও ‘3460’ এর কতগুলো divisor আছে তা বের করে ফেল দেখি!

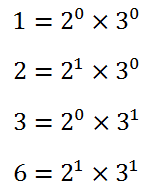
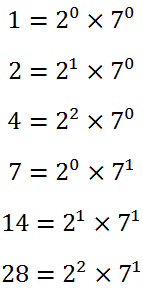

excellent writing on Number theory and Combinatorics. Keep writing.
ধন্যবাদ! 😀