এই জগতের সবকিছুকে সংখ্যা দিয়ে প্রকাশ করার এক ইচ্ছা প্রকাশ করে গিয়েছিলেন পিথাগোরাস সাহেব। অনেকটুকু(!) পেরেছিলেন ও! সংখ্যার ক্ষমতা বিস্তৃত বলেই হাজার বছর আগে এক স্বপ্নবাজ এতবড় স্বপ্ন বুনে গিয়েছেন,আজও আমরা যেই কম্পিউটার,মোবাইল ফোন থেকে শুরু করে যত যন্ত্রপাতি ব্যবহার করি,সবকিছুর পিছনেই একটি ভাষা একচ্ছত্র আধিপত্য বিস্তার করে আছে,যার নাম ”সংখ্যা”। আজকের পর্বে আমরা এই সংখ্যা নিয়েই শিখবো। খুব ছোট এই পর্বটিতে থাকছে বহুল প্রচলিত কিছু সংখ্যার সিস্টেম,তাদের মাঝে রুপান্তর,কেনই বা কয়েকজনের আবিষ্কার হলো – এগুলো।
সৃষ্টির সূচনালগ্ন থেকেই মানুষ গণনার প্রয়োজনীয়তা অনুভব করতে থাকে। শিকারের জন্য,নিজেদের সম্পত্তির দেখভাল এবং হিসাব নিকাশের জন্য,গণনা ছাড়া এগুলো তো অসম্ভব! তো ওই যুগে মানুষ গণনার জন্য তাদের আঙ্গুলের ব্যবহার শুরু করলো। এক,দুই,তিন… এভাবে তারা দশ এর বাইরে আর গুণতে পারতোনা! কারণ টাও খুব সহজ,হাতে তো দশের বেশি আঙ্গুল নেই! 😀 দুই হাত মিলে আর কি। সংখ্যার ইতিহাস নিয়ে বেশি কিছু বলতে চাচ্ছিনা,আমার এই পর্বটি মূলত ভিত্তি রুপান্তর নিয়ে,তাও একটু খানি বলে নিলাম। যাদের আগ্রহ আছে,তারা দু’টি ভিডিও দেখে আসতে পারেন। কাজে দিবে!
আজকের এই পর্বে আমরা আলোচনা করবো দশ ভিত্তিক , দুই ভিত্তিক, আট ভিত্তিক এবং ষোল ভিত্তিক এই চার প্রকারের নাম্বার নিয়ে। শুরু করা যাকঃ
দশ ভিত্তিক সংখ্যা বা Decimal Number System :
”ভিত্তি” মানে হচ্ছে,একটি সংখ্যাব্যবস্থা মূলত কয়টি ডিজিট বা অংক নিয়ে কাজ করে,সেটা। এই দশ ভিত্তিক সংখ্যা ব্যবস্থা কাজ করে ”দশটি” অংক নিয়ে। এরা হচ্ছেঃ ০ , ১ , ২ , ৩ , ৪ , ৫ , ৬ , ৭ , ৮ , ৯ । এবং এর মাধ্যমেই আমরা আমাদের দৈনন্দিন জীবনের সকল কাজকর্ম চালিয়ে থাকি। 🙂 যেকোনো প্রকারের সংখ্যাকে রিপ্রেজেন্ট করতে দশ ভিত্তিক সংখ্যা মানুষের জন্য সবচেয়ে বেশি উপযোগী।
একটি সংখ্যা ধরা যাক ”৫৪৬২” । দশ ভিত্তিক সংখ্যা ব্যবস্থায় এখানে,
৫ হচ্ছে ”সহস্রের ঘরের অংক”
৪ হচ্ছে ”শতকের ঘরের অংক”
৬ হচ্ছে ”দশকের ঘরের অংক”
২ হচ্ছে ”এককের ঘরের অংক”
এই একক দশক শতক এসব ঘরের কিছু বৈশিষ্ট্য আছে। এই যে যেমন ধরো এককের ঘরের ক্ষমতা হচ্ছে ১,দশকের ঘরের ক্ষমতা হচ্ছে ১০,শতকের ঘরের ১০০,সহস্রের ঘরের হচ্ছে গিয়ে ১০০০। এভাবে অযুত লক্ষ নিযুত কোটি পর্যন্ত প্রতি ঘরের ক্ষমতা ১০ গুণ করে বৃদ্ধি পাচ্ছে,তাইনা? তাই হবে। আচ্ছা,তাহলে উপরের চারটি লাইন থেকে আমরা আমাদের সংখ্যাটায় ফিরে যেতে পারি কিনা একটু দেখে আসিঃ
৫ x ১০০০ = ৫০০০
৪ x ১০০ = ৪০০
৬ x ১০ = ৬০
২ x ১ = ২
এবার এদের যোগ করে পাই ( ৫০০০+৪০০+৬০+২) = ৫৪৬২ 😀 দেখো,এটাই ছিলো আমাদের প্রথমে উল্লিখিত সংখ্যাটি! সব ক্ষেত্রেই দশকের ব্যাপারটি কাজ করছে,ক্রমাগত এর ঘাত এক করে বাড়ছে,এবং এভাবেই দশটি অংক আর এদের বিভিন্ন ঘরের ঘাত নিয়ে এই সংখ্যা ব্যবস্থাটি সাজানো। 🙂 উপরের এই চার্টটা আমরা এবার একটু অন্যভাবে লিখে আসি, বিশ্বাস করো পরে কাজে লাগবে। :3
৫ x ১০^৩ = ৫০০০
৪ x ১০^২ = ৪০০
৬ x ১০^১ = ৬০
২ x ১০^০ = ২
ব্যস,আমার নোট করা শেষ! :’)
দুই ভিত্তিক সংখ্যা বা Binary Number System :
আচ্ছা,এবার আমরা এমন এক নাম্বার সিস্টেমের সাথে পরিচিত হবো,যেই নাম্বারের জগতের সব সম্বল হচ্ছে দু’টি অংক শুধু! এবং এরা হচ্ছে ০ আর ১ । এই দুইটি ডিজিটের নানান রকম কম্বিনেশন দিয়েই এই জগতে সমস্ত নাম্বারকে রিপ্রেজেন্ট করা হয়। একটা দশ ভিত্তিক সংখ্যা ধরলাম ১২,এটা আমরা বাইনারির জগতে কেমন দেখবো সেটা দেখে আসি।
যেহেতু আমরা দুই এর ভিত্তির একটি নাম্বার সিস্টেমে ১২ কে নিয়ে যাচ্ছি,তাই এঁকে আমরা ক্রমাগত ২ দিয়ে ভাগ করতে থাকবো। এবং ঠিক ততক্ষণ আমাদের এই প্রসেস অব্যাহত থাকবে,যতক্ষণ পর্যন্ত ভাগফল ১ বা শুণ্য ( এক কথায়,২ এর চেয়ে ছোট) না হচ্ছে। 😀 এবং এই যে প্রতি স্টেপে আমরা ভাগ করতে থাকবো,এই ভাগের প্রক্রিয়াতে যেই ভাগশেষগুলো আমরা পাবো,সেগুলোকে আরেকটি বক্সে সারিবদ্ধভাবে সাজাতে থাকবো। ^_^
 চিত্রে দেখো,আমরা সবার শেষে ভাগফল পেয়েছি ১,তখনি আমাদের কাজ শেষ করে দিয়েছি এবং এই সর্বশেষের ভাগফলটিকে সঙ্গে নিয়ে অবশিষ্ট ভাগশেষগুলোকে সঙ্গে নিয়ে ( নিচ থেকে উপরে ) একটি ১ আর ০ এর কম্বিনেশনের সংখ্যা পেয়ে গেছি! যা হচ্ছে 1100 😀 বিশ্বাস করো,১২ এর বাইনারী ভার্সন কিন্তু 1100 😀 ( নোকিয়া ১১০০ এর কথা কার কার মনে পড়লো হাত উঠাও তো! :v )
চিত্রে দেখো,আমরা সবার শেষে ভাগফল পেয়েছি ১,তখনি আমাদের কাজ শেষ করে দিয়েছি এবং এই সর্বশেষের ভাগফলটিকে সঙ্গে নিয়ে অবশিষ্ট ভাগশেষগুলোকে সঙ্গে নিয়ে ( নিচ থেকে উপরে ) একটি ১ আর ০ এর কম্বিনেশনের সংখ্যা পেয়ে গেছি! যা হচ্ছে 1100 😀 বিশ্বাস করো,১২ এর বাইনারী ভার্সন কিন্তু 1100 😀 ( নোকিয়া ১১০০ এর কথা কার কার মনে পড়লো হাত উঠাও তো! :v )
একটু ভেরিফাই করি। আমরা এবার এই বাইনারী নাম্বারটিকে আবার ডেসিমেলে রুপান্তর করে দেখতে চাই। এখন আবার ১১০০ কে দশ দিয়ে ভাগ করা শুরু করে দিয়োনা কিন্তু! এই ”ভাগ করে আরেক নাম্বার সিস্টেমে যাওয়া” সেটা শুধুমাত্র দশ ভিত্তিক ( Decimal ) সংখ্যা থেকেই যাওয়া যায়। অন্য যেকোনো নাম্বার কে দশ ভিত্তিকে রুপান্তর করে,তারপরে আমরা চাইলে সেটা থেকে যেকোনো নাম্বার সিস্টেমে জাম্প করতে পারি। 😀 তো আগে তো জানতে হবে,অন্য একটা নাম্বারের জগত থেকে কোন রাস্তা ধরে হাঁটলে আমরা দশমিক সংখ্যার ( আমাদের জগত যেটা ) জগতে প্রবেশ করতে পারবো! চলো তাহলে রাস্তাটা চিনে আসি! 😀
চিত্রে r এর পরিচয়টা দেয়া হয়নি। r হচ্ছে আমরা যেই নাম্বার সিস্টেমের সংখ্যাটাকে ডেসিমেলে নিচ্ছি,তার অংক সংখ্যার চেয়ে ১ ছোট এমন একটি সংখ্যা। 😀
আমরা কি তাহলে (১১০০)২ কে ডেসিমেলে নিয়ে যেতে পারবোনা? 😀 চলো দেখিঃ
( 1 x 2^3) + ( 1 x 2^2) + ( 0 x 2^1) + ( 0 x 2^0)
= 8 + 4 + 0 + 0
= 12
পেয়ে গেলাম 😀 এখানে ১২ কে লিখা হয় এভাবেঃ (১২)১০
মানে সংখ্যাটা যেই ভিত্তির অন্তর্ভুক্ত , তাকে নিচে ছোট করে লিখে দেয়া হয়।
আট ভিত্তিক সংখ্যা বা Octal Number System :
খুব স্বাভাবিক। এই সিস্টেমে ডিজিট থাকবে ”আট” টা। এবং এরা হচ্ছেঃ
0 1 2 3 4 5 6 7
মোট অংক তাহলে পেলাম আটটা। আচ্ছা,(১২)১০ নিয়েই আমাদের সব খেলা চলুক! 😀 (১২)১০ কে আমরা আট ভিত্তিক সংখ্যায় পরিণত যদি করতে চাই,তাহলে কত দিয়ে একে ভাগ করতে থাকবো? তোমাদের উত্তর যদি ”আট” হয়,তাহলে স্বাগতম! এই প্রক্রিয়ার চেহারা যেমন হবেঃ
বলোতো,উত্তর কতো হবে? শেষ ভাগফলটা সহ কাউন্ট করতে হবে,তাই এর Octal representation হবেঃ (12)10 = (14)8
এটিই হওয়ার কথা ছিলো। কারণ অক্টাল নাম্বার সিস্টেমে ৭ এর পরে আসবে ১০ ( কারণ ৮ আর ৯ অক্টাল সিস্টেমেই নাই! ) তারপরে আসবে ১১ , তারপরে ১২,তারপরে ১৩ আর তারপরে ১৪। ৮ আর ৯ থাকলে,এটি হতো আরো দুই কম। তখন ১৪ না হয়ে হতো ১২,যেটি দশ ভিত্তিক সংখ্যাটি ছাড়া আর কিছু নয়। 🙂
ষোল ভিত্তিক সংখ্যা বা Hexadecimal (Hex) Number System :
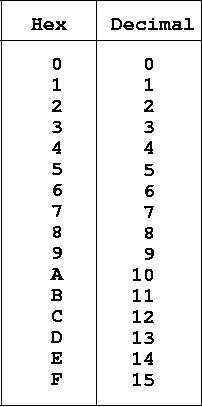
এই সিস্টেমে ডিজিট থাকবে ১৬ টি। এরা হচ্ছেঃ
এই সিস্টেমে আমাদের সেই দশ ভিত্তিকের ১২ সংখ্যাটিকে কনভার্ট করার প্রয়োজনই নাই। কারণ ১২ নিজেই এই সিস্টেমে আগে থেকেই ডিফল্ট সেট করা আছে,যেটি হচ্ছে C | আমরা একটু বড় টাইপের একটা নাম্বারকে Hex এ নিয়ে দেখি,কেমন? এবার আমি উত্তরটা লিখে দিবো,ভাগের কাজটি আগের দু’টি এক্সামপলের মতো করে তোমরা নিজেরা চেষ্টা করে দেখবে।
(124)10 = (7C)16
আচ্ছা,A B C D এগুলো দেখে ভয় পাওয়ার কোনো দরকার নেই। ভাগশেষগুলো যখন ৯ এর চাইতে বড় আসবে ( সবসময় ১৫ বা এর নিচেই থাকবে,ভয় নেই ) তখন শুধু লিখার সময় এর corresponding letter টি লিখে দিবে। ঠিকাছে? 😀
দু’টো জীবন বাঁচানো শর্টকাটঃ
১) বাইনারী থেকে হেক্স / হেক্স থেকে বাইনারী
১) বাইনারী থেকে অক্টাল / অক্টাল থেকে বাইনারী
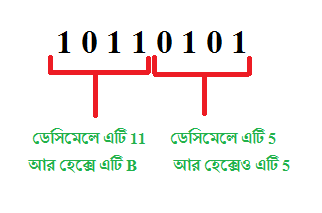
১) আমরা চাইলে খুব সহজেই খুব্বব্ববি সহজে বাইনারী থেকে এক লাফে হেক্সে চলে যেতে পারি। এর জন্য আমাদের করণীয় কাজটি হচ্ছে যে সংশ্লিষ্ট বাইনারী নাম্বারটিকে শেষ থেকে চারটি চারটি ডিজিট নিয়ে গ্রুপ তৈরী করে ফেলা,তারপরে সেই নাম্বারগুলোর corresponding হেক্স ভ্যালু বসিয়ে দেয়া। একটা উদাহরণ দেখিঃ
সুতরাং!!!!! (10110101)2 একে হেক্সে নিয়ে গেলে পাবো আমরা (B5)16 , Isn’t it cool?
তোমরা চাইলে বাইনারী নাম্বারটাকে ডেসিমেলে নিয়ে আবার সেটাকে হেক্সে নিয়ে চেক করে দেখতে পারো। ডেসিমেলে এই বাইনারী সংখ্যাটা হচ্ছে 181
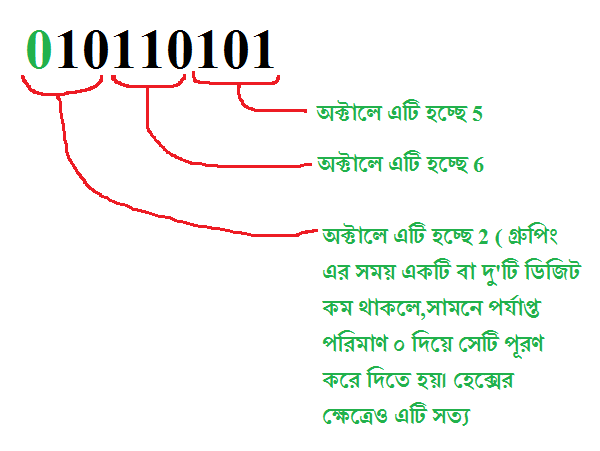
২) সেইম একটি ঘটনা ঘটে বাইনারী থেকে অক্টালে যাওয়ার ক্ষেত্রেও! তবে এবার গ্রুপিং চারটা ডিজিট না,৩ টি নিয়ে করতে হয়। আর তারপর ৩ ডিজিটের যেই বাইনারী নাম্বারটা পাবো,তার corresponding digit অক্টালের ডিজিট লিস্ট থেকে বসিয়ে দিলেই কাজ শেষ! এটাও করে দেখাতে হবে? আচ্ছা দেখাই আগের উদাহরণ দিয়েই!
তাহলে, 10110101 এর অক্টাল রিপ্রেজেন্টেশন হবে 265 😀 চেক করে দেখো সবাই কিন্তু! তাহলেই আসল মজাটা পাওয়া যায়। 😀
ও হ্যাঁ, হেক্স সিস্টেমের আবিষ্কারের পেছনের মূল কারণ হচ্ছে,বিশাল বিশাল বাইনারী নাম্বারকে সহজে মনে রাখার নিমিত্তে। দেখো,বিশাল একটা বাইনারী নাম্বার চিন্তা করি আমরা,যেমনঃ 1110110011111 ,এবং এর হেক্সাল রিপ্রেজেন্টেশনটা হচ্ছে 1D9F 😀 কি,বাইনারীর চেয়ে সহজ না?
আমরা চেষ্টা করবো পরের পর্বে BCD,ASCII এসব নিয়ে কিছু আলোচনা করতে। কোনো প্রশ্ন থাকলে কমেন্ট বক্সে জানাতে ভুলো না। আজকের মতো টাটা বাই বাই।




৫ ভিত্তিকে ১১০,১০ ভিত্তিকে কত?